Króliczy początek

Mimo, że pierwsze wzmianki o serii liczb nazywanej dziś „ciągiem Fibonacciego” są jeszcze z przed naszej ery, to na stary kontynent ciąg ten przybył wraz Leonardem z Pizy. Legendy mówią, że Fibonacci posłużył się nim, aby rozwiązać problem rozrodu królików, przy okazji zatrzymując go na stałe w Europie. Osławiona seria liczb została opisana w dziele Fibonacciego „Liber Abaci” – księdze kalkulacji. Leonardo pokazał ją rozwiązując problem rozrodu wyidealizowanych królików. Było to pierwsze miejsce użycia złotej proporcji w naturze.

Sens zadania przedstawia się tak:
Ile par królików może spłodzić jedna para w ciągu roku, jeśli:
1. Na początku mamy jedną parę królików
2. Każda para rodzi nową parę po miesiącu.
3. Króliki łączą się (para staje się płodną) po miesiącu.
4. Króliki nie umierają.

Najlepiej jest to sobie zwizualizować graficznie. Jeden królik w wierszu symbolizuje jedną parę.

Rozród pszczół

Okazuje się, że nie tylko wyidealizowane króliki rozmnażają się zgodnie z ciągiem Fibonacciego. Kolejnym przykładem są pszczoły miodne. Musisz wiedzieć, że samica tego owada wykluwa się z zapłodnionego, przez samca, jaja matki pszczelej. Natomiast truteń – samiec pszczoły – wykluwa się z jaja niezapłodnionego. Przyjrzyjmy się teraz drzewu genealogicznemu trutnia.

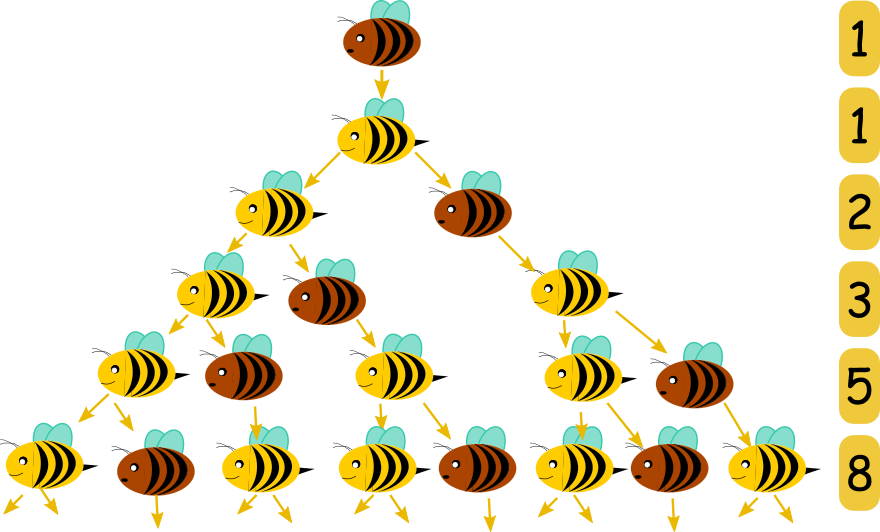
Skoro truteń powstał z jaja niezapłodnionego, ma tylko matkę. Z kolei ona musiała mieć i matkę, i ojca. Dlatego w trzecim wierszu są już dwa symbole (samca i samicy). Schemat powtarza się w kolejnych pokoleniach – bezpośrednim przodkiem każdego trutnia jest samotna samica, a każda samica ma dwoje rodziców. Na grafice widać jak powstaje ciąg Fibonacciego.

Spirala pędów

Kolejnymi przykładami występowania złotej liczby w naturze są rośliny, a dokładniej ich ulistnienie. Liście z jednego miejsca łodygi mogą wyrastać podwójnie, potrójnie lub więcej. Często układają się wtedy naperzeciwlegle, nakrzyżlegle itp. Jednak gdy liście wyrastają pojedynczo z jednego więzła układają się w kształt helisy/spirali wokół łodygi. To ulistnienie nazywamy skrętoległym.

Dzieje się tak ponieważ rośliny dążą do pochłaniania jak największej ilości światła. W tym celu ustawiają swoje liście tak, aby jeden nie zasłaniał drugiego, rzucając na niego cień. Z matematycznego punktu widzenia najlepszym ułożenie jest wtedy, gdy kąt między kolejnymi liśćmi będzie liczbą niewymierną. Zmniejsza to szansę na ustawienie się ich w pionowej linii jeden pod drugim (w jednej prostnicy).

Kąt ten nazywamy kątem dywergencji. Dywergencja to stosunek liczby obrotów helisy, między liśćmi w jednej prostnicy, do liczby mijanych po drodze liści. Kąt obliczamy mnożąc ten stosunek przez $360^\circ$.

Okazuje się, że u znacznej ilości roślin dywergencja wyraża się w liczbach ciągu Fibonacciego, a kąt dywergencji jest bliski złotemu kątowi. Jednak reguła ta nie powtarza się u wszystkich roślin skrętoległych.

$\frac{1}{2}$ - wiązy, lipy, niektóre trawy, $\frac{3}{8}$ - astry, kapusta, topole, grusze. $\frac{1}{3}$ - olchy, brzozy, turzyca, buki, jeżyny, leszczyny $\frac{2}{5}$ - róże, dęby, morele, wiśnie, jabłonie, starzec zwyczajny $\frac{8}{21}$ - jodły, świerki $\frac{5}{13}$ - wierzby, migdałowce

Zastanawiałeś się dlaczego tak trudno znależć czterolistną koniczynę? Tak się składa, że nie tylko układ liści jest związany ze złota proporcją. U większości rodzajów kwiatów liczba ich płatków też jest wyrazem ciągu Fibonacciego.

Trzeba też pamiętać, że każdy osobnik danego gatunku może mieć jakieś zmiany względem innych. Ciąg Fibonacciego to reguła, a jak wiadomo od każdej reguły istniejeą odstępstwa. ilość liści czy płatków roślin zależy od tak wielu czynników. Od ich wieku, środowiska w jakim żyją itd.

Spirale pośród ziaren

Ułożenie ziaren niektórych roślin też jest kojarzone z liczbami Fibonacciego. Dobrym przykładem jest słonecznik lub szyszka, ale występuje to też u innych roślin z rodziny astrowatych i obrazkowych. Ziarna słonecznika czy zakończenia szyszek układają się w jakby ramiona przypominające spirale, których biegun jest w centrum rośliny. Spirale te najczęściej biegną w dwóch różnych kierunkach. Zgodnie i w przeciwnie do ruchów wskazówek zegara. U znacznej części roślin ilość spiral i w jednym, i w drugim kierunku są równe wyrażeniom z ciągu Fibonacciego. Poniżej część spiral jest oznaczona.

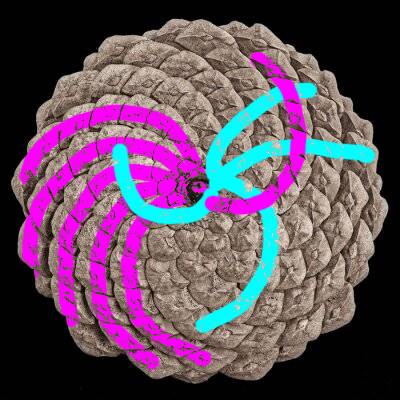
Szyszka świerka pospolitego z grafiki ma 13 spiral w jednym kierunku i 8 w drugim. Szyszka modrzewia czesto ma 5 spiral lewoskrętnych i 3 prawoskrętne, a sosny 5 i 8. Ten słonecznik ma akurat 34 i 21 spiral. Często pojawiają się też kombinacje: 13 i 21, 34 i 55, 55 i 98.

Oprócz tego ułożenie ziaren słonecznika przypomina wcześniej omawiane - przy okazji niewymierności liczby $\varphi$ - siatki punktów. Stały kąt między ramionami jest w przybliżeniu równy $\frac{360^\circ}{\varphi}$. Jego dopełnieniem do kąta pełnego jest złoty kąt. Jest to związane między innymi z liczbą wspomnianych ramion wyrażających się w ciągu Fibonacciego.

Złote proporcje człowieka

Księga rzymskiego architekta Witruwiusza „De architectura” jest bezcennym źródłem wiedzy o architekturze i sztuce budowlanej starożytnych Greków i Rzymian. Znajduje się tam opis człowieka witruwiańskiego - mężczyzny o wyidealizowanych wymiarach. Jego proporcje miały wyznaczać kanon piękna architektonicznego. Około 1500 lat później własną wersję ilustracji „człowieka witruwiańskiego” upowszechnił Leonardo da Vinci. Jak już wcześniej omawialiśmy Leonardo tworzył też rysunki do księgi Luca Pacioliego, związanej ze złotym podziałem. W którymś momencie historii ludzie błędnie połączyli oba fakty.

Stwierdzili, że proporcje idealnego człowieka Witruwiusza są zgodne z boską proporcją. Pomijają przy tym chronologie wydania tych dwóch dzieł („De divina proportione” wydano około 20 lat później) Sam Leonardo tworząc swoją wersję „człowieka witruwiańskiego” umieścił pod swoim rysunkiem podziałkę z użytymi proporcjami oraz tekst je opisujący, które zostały również wyraźnie zaznaczone na rysunku. Ani opis Leonardo, ani opis Witruwiusza nie ma związku ze złotą liczbą. Oczywiście nie można wykluczyć związku ilustracji Leonarda z $\varphi$, gdyż już wcześniej się nią interesował.

Ludzie jednak dalej szukali boskiej liczby w ludzkich proporcjach. I rzekomo znalazł ją Adolfow Zeising opisując to w swojej książce „Neue Lehre von den Proportionen des menschlichen Körpers…” (z niem. „Nowa doktryna dotycząca proporcji ludzkiego ciała” ) Stwierdził on, że: stosunek wzrostu człowieka do odległości od stóp do pępka jest równy złotej proporcji. Trzeba jednak wiedzieć, że jego pomysły występowania złotej proporcji są opisywane enigmatycznie i spotykały się z dużą krytyką innych uczonych.

Na niektórych stronach internetowych opisujących znaczenie złotej proporcji w naturze, można przeczytać informacje typu:

„Człowiek posiada dwie kończyny: górną i dwie dolne. Posiada także pięć zmysłów, trzy otwory w głowie (oczy i usta), trzy wypustki głowy (uszy i nos) oraz w znacznej większości, pojedyncze organy. Idealne ludzkie ciało ma zachowane proporcje zgodne z ciągiem Fibonacciego. Dlaczego? Stosunek wzrostu człowieka do odległości od stóp do pępka, koniuszków palców do łokci, od łokcia do nadgarstka wynosi w każdym przypadku 1,618 .”
https://nauka.uj.edu.pl/aktualnosci/-/journal_content/56_INSTANCE_Sz8leL0jYQen/74541952/140402746

Według mnie jest to bardzo życzeniowe myślenie i wręcz obsesyjne szukanie liczby $\varphi$ wszędzie. Dzisiejsi naukowcy zaprzestali więc juz szukać liczby $\varphi$ w proporcjach ludzkiego ciała. Teraz ich uwagę przyciąga badanie wystepowania złotej liczby węwnątrz ciała człowieka.

• W 2003 Volkmar i Harald Weissowie przeanalizowali dane psychometryczne i rozważania teoretyczne, dochodząc do wniosku, że złoty podział jest podstawą cyklu fal mózgowych. W 2008 zostało to potwierdzone doświadczalnie przez zespół neurobiologów. Tutaj link do pracy Volkmar i Haralda Weissow.


• Kilku badaczy zasugerowało powiązania między złotym podziałem a ludzkim genomem DNA. Odnajdują tam ciąg Fibonnaciego podobnie jak w przypadku królików Fibonacciego czy pszczół miodnych. Uważają, że chromosom X jest dziedziczony w pewnych przypadkach zgodnie z tym ciągiem. Poniżej Linki do dalszej lektury: Krótkie polskie wyjaśnienie zagadnienia oraz Anglojęzycznej Pracy naukowej

Złote mity

Przeglądając różne artykuły, fora internetowe i tym podobne, można się natknąć na nie do końca zgodne z prawdą założenia. Owszem, nie ma w tym nic dziwnego, jednak te same informację na temat złotego podziału znajdują się na stronach edukacyjnych. To już budzi niepokój. Jest to wynik powielania nieudowodnionych i błednych myśli związanych z boską proporcją. Przedstawimy tu sobie tylko kilka najczęściej powtarzanych "złotych mitów".

Jeden z takich mitów już opisaliśmy w zakładce "człowiek". Na wielu stronach edukacyjnych (przykład tutaj), które powinny stanowić rzetelne źródło informacji, opisuję się proporcje ciała ludzkiego jako złote. Autorzy stron często podają tę spekulację jako uniwersalne prawo. Jak już sobie tłumaczyliśmy, nie jest to żaden fakt, a tylko teoria zwiazana z upodobaniem Leonarda da Vinciego do liczby $\varphi$. Nikt jednak tego nie udowodnił. Nie może być to też ogólnoludzka prawda ponieważ każdy człowiek jest inny. Każdy ma inne proporcje ciała, inny wzrost, inną długość rąk, wielkość stopy itd. Nie ma też ustalonych konkretnych miejsc ciała skąd zaczyna się pomiary. Każdy może zmierzyć się na swój sposób. Na pewno każdy miał taką sytuację kiedy mierzył swój wzrost kilkakrotnie i za każdym razem wychodziły inne wyniki:
"Teraz wyszło tyle, ale u pielęgniarki tydzień temu był centymetr więcej"... Pokazuje to absurd tego mitu.

Następnym czesto powtarzanym mitem jest obecność złotej spirali w muszli łodzika. Nie jest to jednak potwierdzone żadnymi głębszymi pomiarami. Już tłumaczyliśmy, że zlota spirala nie jest jednyną spiralą matematyczną. Jest ona tylko rodzajem spirali logarytmicznej i właśnie taki kształt ma muszla łodzika. Na to, że pojawi się tam akurat złota spirala jest bardzo małe prawdopodobieństwo. Grafika obok to przykład muszli łodzika z naniesioną złotą spiralą. Nawet gdy ją przeskalujemy, nie będzie zbytnio pasować do kształtu muszli.

Drugie zdjęcie też jest opisywana jako złota spirala. Jednak jest to spirala Fibonacciego która nie jest spiralą logarytmiczną. Takiej spirali nie znajdziemy w muszlach!

Poza tym każdy łodzik ma swoje indywidualne cechy, tak jak człowiek. Poszczególne osobniki mają różne wymiary muszli i w nie każda będzie przecież pasowała do złotej spirali.

Często można przeczytać też o mitach dotyczących ukladu słonecznego. Mowi się że stosunek odległości od odpowiednich planet układu slonecznego jest równy zlotemu podziałowi. Dobrze skomentował to profesor Piotr Sułkowski na forum "Zapytaj Fizyka":

"Oczywiście, że wśród miliardów gwiazd i miliardów galaktyk można dopatrzyć się różnych proporcji, w szczególności tzw. boskiej proporcji, zwanej też złotym podziałem. Zależności takie są jednak przypadkowe i nie należy przywiązywać do nich szczególnej wagi. Innym przykładem próby odniesienia własności ciał niebieskich do geometrii była np. teoria Keplera, opisana w dziele Mysterium Cosmographicum, w którym dowodził on, że orbity planet w Układzie Słonecznym można wpisać w bryły foremne"

W filmie "Pi" z 1998 roku, reż. Darren Aronofsky padł taki cytat:

"Jeśli obsesyjnie czegoś szukasz, twój mózg przefiltruje rzeczywistość w taki sposób, że odnajdziesz to gdziekolwiek."

W zupełności można się z tym zgodzić. Autorzy niektorych artykułów ulegają takiej obsesji i wpisują $\varphi$ i złotą spiralę gdziekolwiek się da. Znajdują ją w huraganach, budowie zwierząt i roślin, w falach i wiele wiele innych. Przykładów jest bardzo dużo, a niestety dowodów na ich prawdziwość znacznie mniej. Dla internautów nieraz wystarczy tylko znalezienie, gdzieś przypadkiem liczby 1,6 aby zwierze, obraz, roślina, rzeźba, planeta stała się "złotym przykladem"