Złoty podział fascynował uczonych już od co najmniej 2400 lat. Wszystko zaczęło się od badań starożytnych Greków, którzy zauważyli jego częste występowanie w geometrii, a szczególnie w konstrukcji pentagramów i pięciokątów foremnych. Około 300 lat p.n.e Euklides z Aleksandrii (aby dowiedzieć się więcej kliknij w zdjęcie) w swoich „Elementach” wyjaśnia podział odcinka w złoty sposób:

jeżli $a + b = 1$ (czyli całemu odcinkowi), to \(1 - a = b\). Rozwiążmy równanie:

W połowie II wieku n.e. Włoski matematyk Luca Pacioli wydał księgę zatytułowaną: „De Divina Proportione” (łac.„Boska Proporcja”). Jest to matematyczne dzieło ilustrowana przez Leonarda da Vinci, które bada zastosowania złotego podziału w różnych sztukach.

Pacioli w treści dzieła podaje pięć powodów dlaczego złoty podział powinnien być przedstawiany jako "boski":

Mimo, że ciąg Fibonacciego jest najczęściej utożsamiany z boską proporcją, to nie jest on jedyny. Okazuje się, że każda seria liczb, w której każdy następny wyraz jest równy dwóm poprzednim wyrazom także jest zbieżna do liczby Phi. Na przykład:
Ciąg XYZ: \(\;\varphi_n = \frac{a_n}{a_{n-1}} = \frac{b_n}{b_{n-1}}\)

Teraz sam możesz wymyśleć swój własny ciąg i sprawdzić tą zależność. Wyrazy ciągu mogą być dowolną liczba rzeczywistą.

Ciąg Lucasa to, po ciągu Fibonacciego, najbardziej znany ciąg powstały na podobnej zasadzie. Lucas poświęcił sporo czasu na badanie ciągu Fibonacciego i stworzył ciąg jeszcze bliżej związany ze złotą proporcją. Odpowiedział na pytanie co się stanie gdy zaokrąglimy kolejne potęgi złotej liczby:

Zauważ, że kolejne wyniki zaokrągleń powstają po zsumowaniu dwóch poprzednich. Tak powstał Ciąg Lucasa o kolejnych wyrazach:

Oczywiście: \[\lim_{n\to\infty}\frac{L_{n}}{L_{n-1}} = \varphi\]

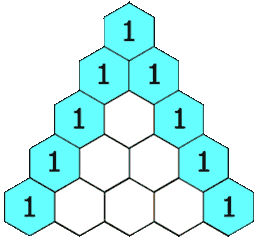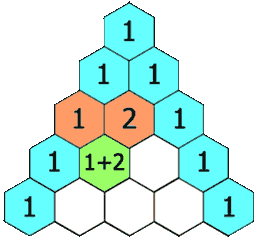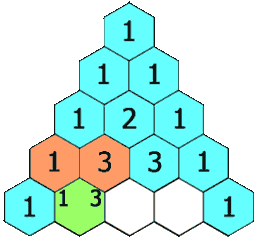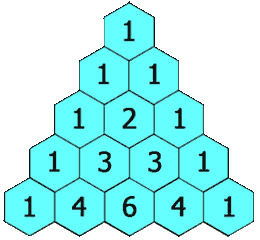
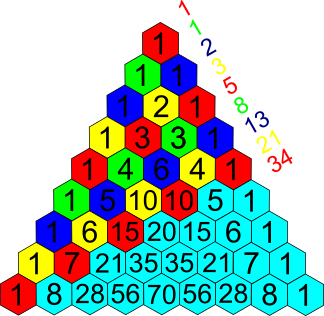
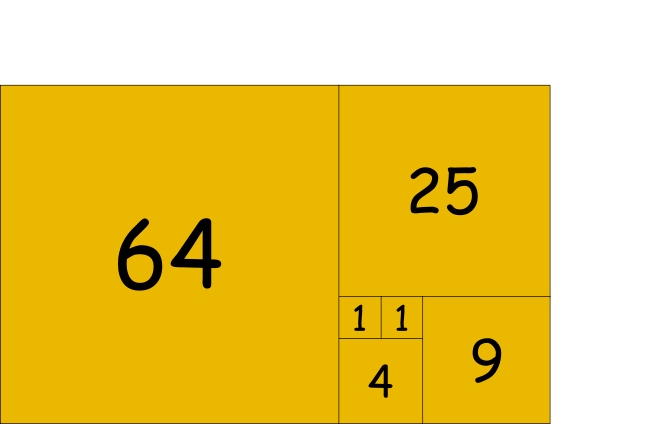
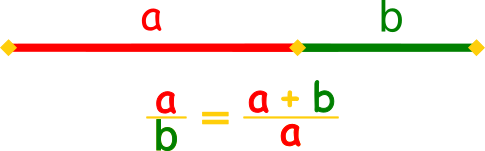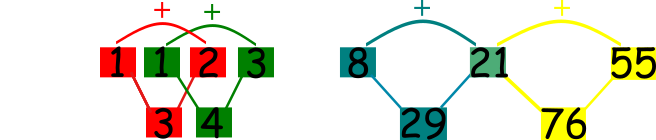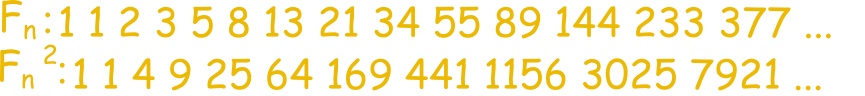Zaobserwuj co się stanie kiedy zestawimy ze sobą ciąg Fibonacciego i Lucasa:

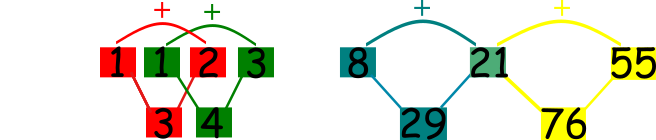
Zauważ, że zachodzą równości:

$L_{n}=F_{n-1}+F_{n+1}$
$F_{n}={\tfrac {1}{5}}(L_{n-1}+L_{n+1})$
$ F_{n+1}= \tfrac {1}{2} (F_{n}+L_{n})$

Jest to przykład fraktalnej natury ciągu. Fraktal to rodzaj figury geometrycznej charakteryzującej się własnością samopodobieństwa — małe fragmenty fraktala, oglądane w odpowiednim powiększeniu, wyglądają tak samo jak obiekt pierwotny. W przypadku tych dwóch ciągów udało nam się dokonać zamiany transponowania jednego ciągu w drugi zgodnie z regułą samopodobieństwa. Poniżej znajdują się przykłady fraktali.

Pewnie już zauważyłeś, że $\varphi$ jest niewymierną liczbą. Treaz wyprowadzimy kilka dowodów potwierdzających twoje obserwacje

Skoro już udowodniliśmy niewymierność $\varphi$, zastanówmy się jak dobrze daje się przybliżać liczbami wymiernymi. Przyjrzyj się grafiką.

Pokazują one w jaki sposób układają się kolejne punkty, gdy umieszczamy je coraz dalej od środka jednocześnie obracając je o pewien stały kąt wokół niego.
Po prawej stronie obrót jest o $\frac{360^\circ}{\varphi}\approx 222.5^\circ$. Wartość ta jest dopełnieniem złotego kąta do kąta pełnego: $360^\circ - 222.5^\circ = 137.5^\circ$.
Po lewej dla porównania mamy obrót o $\frac{360^\circ}{\pi}\approx 114.6^\circ$.

Widać wyraźnie, że w przypadku obrotu o $\pi$-tą część kąta pełnego kolejne punkty układają się w 22 jakby ramiona. Zbliżony obraz otrzymalibyśmy, gdyby obrót był po prostu o $\frac{1}{22}$ kąta pełnego. Sugeruje to, że $\pi$ jest bliska liczbom wymiernym. W przypadku obrotu o kąt $\frac{360^\circ}{\varphi}$ aż takiej bliskości nie dostrzegamy.

Prowadzi to do wniosku, że $\varphi$ jest skrajnie niepodobna do liczb wymiernych. Obrót o ten kąt skutkuje znacznie optymalniejszym rozlokowaniem punktów niż obrót o $114,6^\circ$. ta sama przestrzeń jest lepiej zagospodarowana. Często tłumaczy się tym przyczynę występowania $\varphi$ w ułożeniu ziaren niektórych roślin.

Dodając do siebie poszczególne wyrazy z trójkąta Pascala otrzymujemy kolejne wyrazy ciągu Fibonacciego. Wyrazy te ustawiają się w jednej lini po "ukosie". dla lepszej przejrzystości na rysunku powyżej linie te są oznaczone odrębnymi kolorami.

Wiadomo, że liczby stojące w n-tym wierszu to kolejne współczynniki dwumianu Newtona – rozwinięcia \((a+b)^{n}\). Na przykład W wierszu 5 na miejscu 2 stoi 10 co jest równe \({5 \choose 2}\). Wynika z tego fakt, że kolejne liczby ciągu fibonacciego także możemy zapisać w postaci symbolu Netwona. Na przykład: \(F_6 = 8 = 1 + 4 + 3 = {5\choose 0} + {4\choose 1} + {3\choose 2}\).

Jeśli spotengujemy kolejne wyrazy ciągu Fibonacciego, to powstanie taka seria:

Przyglądając się bliżej tym dwóm ciągom zauważymy, że suma kolejnych wyrazów ciągu ${F_n}^2$ jest równa iloczynowi dwóch kolejnych wyrazów ciągu fibonacciego: $$\sum_{n = 0}^{\infty}{F_n}^2 = F_n \cdot F_{n+1}$$ Na przykład: $$1+1+4 = 6 = 2 \cdot 3$$ $$1+1+4+9 = 15 = 3 \cdot 5$$ $$1+1+4+9+25+64 = 104 = 8 \cdot 13$$

Teraz spóbujmy przedstawić to w formie grafiki. Skupmy się na pierwszych 6 wyrazach ciągu.

Powstałą figurę nazywamy złotym prostokątem. W tym wypadku pole prostokąta jest równe polu mniejszych kwadratów: $64 + 25 + 9 + 4 + 1 + 1 = 104$ lub iloczynowi długości jego boków: $13 \cdot 8 = 104$. Rysunek potwierdza regułę. Dzieląc długości jego boków przez siebie dostajemy złotą liczbę: $13 : 8 = 1.625 \approx \varphi$. Im większy prostokat tym to przybliżenie będzie dokładniejsze.