|
Równania Eulera-Lagrange'a:
Przy odpowiednich zależnościach
otrzymujemy końcowy wzór na funkcję Eulera-Lagrange’a
wyrażającą się następująco:
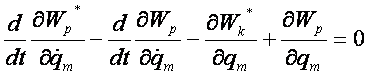
Przy
czym drugi człon równy jest zeru, gdyż energia potencjalna
nie jest funkcją
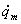 .
Dodając do powyższego równania z lewej strony siły zasilania
zewnętrznego i siły dyssypacji m-tego elementu otrzymamy
rozszerzone równaniu dla układów niezachowawczych i
dyssypatywnych. .
Dodając do powyższego równania z lewej strony siły zasilania
zewnętrznego i siły dyssypacji m-tego elementu otrzymamy
rozszerzone równaniu dla układów niezachowawczych i
dyssypatywnych.
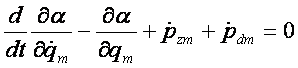
gdzie jest
siłą, mementem bądź napięciem zasilania, zaś jest
siłą, mementem bądź napięciem zasilania, zaś
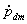 siłą
dyssypacji wyrażającą się spadkiem napięcia na rezystancjach
w obwodzie elektrycznych, i oporami tarcia w ruchu
mechanicznym. siłą
dyssypacji wyrażającą się spadkiem napięcia na rezystancjach
w obwodzie elektrycznych, i oporami tarcia w ruchu
mechanicznym.
 |