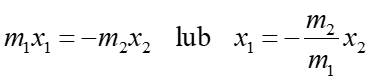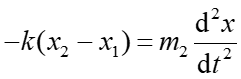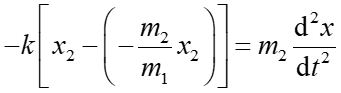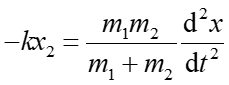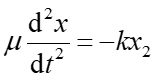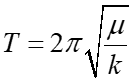Drgania dwóch ciał

W przykładzie przedstawiającym prosty oscylator harmoniczny, rozważaliśmy ciało o masie m przymocowane do sprężyny, poruszające się po poziomej powierzchni. Drugi koniec sprężyny był zamocowany do nieruchomej ściany (rysunek-animacja 12.1) i nie zmieniał swojego położenia i zmiana długości sprężyny równa była przemieszczeniu masy m. Tymczasem w przyrodzie mamy często do czynienia z drgającymi układami dwu lub więcej ciał. Najprostszym przykładem mogą być cząsteczki dwuatomowe na przykład cząsteczka tlenku węgla CO. Możemy sobie wyobrazić, że taki układ jest reprezentowany przez dwie masy połączone nieważką sprężyną tak jak na rysunku-animacji poniżej. W tym modelu sprężyna przedstawia oddziaływania międzycząsteczkowe.

Kliknij w dowolnym miejscu na rysunku żeby uruchomić animację. Ponowne kliknięcie oznacza powrót do początku.

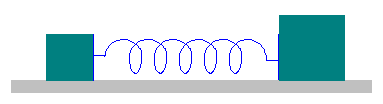
Rys. 1. Układ dwóch mas połączonych sprężyną

Przyjmijmy, że x₁ oznacza przesunięcie masy m₁ od położenia równowagi, a x₂ jest odpowiednim przesunięciem drugiej masy m₂. Ponieważ na układ nie działają żadne siły zewnętrzne więc środek masy układu pozostaje nieruchomy (rozdział 9.2). Zatem

(1)

Zastosujmy teraz do wybranej masy na przykład m₂ drugą zasadę dynamiki Newtona: . Siłą wypadkową, działającą na m₂ jest siła F = −k(x₂ − x₁) gdzie (x₂ − x₁) jest wypadkowym rozciągnięciem sprężyny

(2)

Łącząc równania (1) i (2) otrzymujemy

(3)

lub

(4)

Równanie to możemy zapisać w postaci

(5)

gdzie 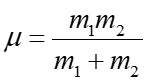jest tak zwaną masą zredukowaną . To równanie ma taką samą postać jak równanie (12.3) więc i takie samo rozwiązanie. Stąd okres drgań układu dwu cząstek jest dany wzorem analogicznym do (12.9)

(6)

Okazuje się, że ruch drgający dwu ciał można opisać tymi samymi równaniami, które wprowadziliśmy dla pojedynczego ciała. Jedno ciało porusza się względem drugiego tak jakby to drugie było nieruchome, przy czym jego masa jest równa masie zredukowanej.