Ćwiczenie 6

Stabilność układów regulacji

Program ćwiczenia

1. Zbudować w Simulink-u układ zamknięty jak na rys.1 i zbadać jego stabilność.

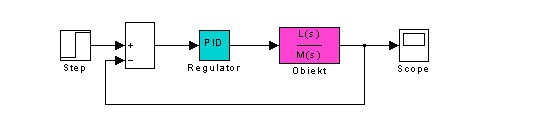
Rys. 1. Schemat układu zamkniętego regulacji

2. Należy obliczyć transmitancję układu otwartego G_o(s) i zamkniętego G_z(s),

dla następujących wartości parametrów

Wejścia: Xzd = 100;

Obiektu G(s): L(s) = 3; M(s) = 6s² +5s+1

Regulatora G_R(s): k = 2.4; T_i = 0.5; T_d = 3; T = 0.12

Wyznaczyć pierwiastki równania charakterystycznego Mz(s) = 0 układu zamkniętego, poleceniem roots (warunkiem koniecznym i dostatecznym stabilności układu liniowego jest, aby pierwiastki równania charakterystycznego miały części rzeczywiste ujemne).

3. Za pomocą kryterium Hurwitza zbadać, dla jakiego zakresu czasu izodromu Ti, układ zamknięty jest stabilny.

Utworzyć wyznacznik Hurwitza złożony ze współczynników wielomianu mianownika transmitancji układu zamkniętego M_z(s). Kryterium Hurwitza orzeka, że pierwiastki równania charakterystycznego M_z(s) = 0, mają części rzeczywiste ujemne, gdy wszystkie współczynniki tego równania istnieją i mają jednakowe znaki oraz wszystkie podwyznaczniki, wyznacznika głównego Hurwitza, są dodatnie. Korzystając z kryterium Hurwitza należy znaleźć szukany zakres wartości T_i, dla którego układ zamknięty jest stabilny.

Obliczyć wartości podwyznaczników przyjmując podane wartości parametrów układu, w szczególności przyjąć, Ti = 0.5, do obliczeń można zastosować polecenie det.

4. Zbadać stabilność układu zamkniętego za pomocą kryterium Nyquista.

Wykonać charakterystykę amplitudowo – fazową układu otwartego poleceniem nyquist, i zaobserwować położenie punktu o współrzędnych (-1, j0) względem charakterystyki Nyquista przy zwiększaniu częstotliwości od zera do nieskończoności.

5. Wyznaczyć zapas stabilności.

W tym celu należy wykonać logarytmiczne charakterystyki amplitudową i fazową układu otwartego za pomocą polecenia margin.

Uwaga! Do realizacji ćwiczenia utworzyć m-pliki (podobnie jak w przykładach Stab1.m, Stab2.m, Stab4.m).

Sprawozdanie

W sprawozdaniu należy zamieścić schemat blokowy układu zbudowany w Simulink–u i wykresy przebiegów regulacji. Zamieścić obliczone transmitancje układów: otwartego i zamkniętego. Podać obliczone miejsca zerowe równania charakterystycznego układu zamkniętego i uzasadnić, w oparciu o wzory Heaviside’a, warunek stabilności asymptotycznej. Opisać kryterium stabilności Hurwitza oraz zamieścić obliczenia przedziału wartości czasu izodromu, dla którego układ zamknięty jest stabilny. Objaśnić kryterium stabilności Nyquista, na przykładzie badanego układu. Pokazać związek pomiędzy kryterium Nyquista opartym na charakterystyce amplitudowo – fazowej, a kryterium opartym na charakterystykach logarytmicznych.