Krzywe Stożkowe

spis treści

co nazywamy hiperbolą

Gdy w ostatniej konstrukcji ukazującej elipsę jako miejsce geometryczne środków okręgów, punkt A znajdzie się poza kołem o środku S, wówczas środki tych okręgów wykreślą hiperbolę. Przyglądając się bliżej można odkryć definicję, jaką spełniają punkty tej hiperboli. Widać, że:
||PS| - |PA|| = |PM| + |PS| - |PA| = |PM| + |PA| - |PA| = |PM| = dł prom okręgu = const.

animacja pokazująca hiperbolę jako miejsce geometryczne środków okręgów stycznych do ustalonego okręgu, przechodzących przez punkt zewnętrzny koła tego okręgu — Hiperbola jako miejsce geometryczne środków okręgów stycznych do ustalonego okręgu, przechodzących przez punkt zewnętrzny koła tego okręgu

Tak więc hiperbolę możemy rozumieć jako krzywą, będącą zbiorem takich punktów, dla których wartość bezwzględna różnicy odległości tych punktów od dwóch punktów nazywanych ogniskami jest stała. Tutaj ogniskami są punkty S i A.

hiperbola z przecięć dwóch okręgów

Hiperbolę możemy skonstruować z przecięcia dwóch okręgów. W jednym z nich promień zmienia się w zakresie <0,r>, drugi okrąg ma promień r + a, gdzie a = const. Punkty wspólne tych okręgów zakreślają hiperbolę. Na poniższej animacji widzimy tylko jedno ramię hiperboli, aby animacja była bardziej czytelna.

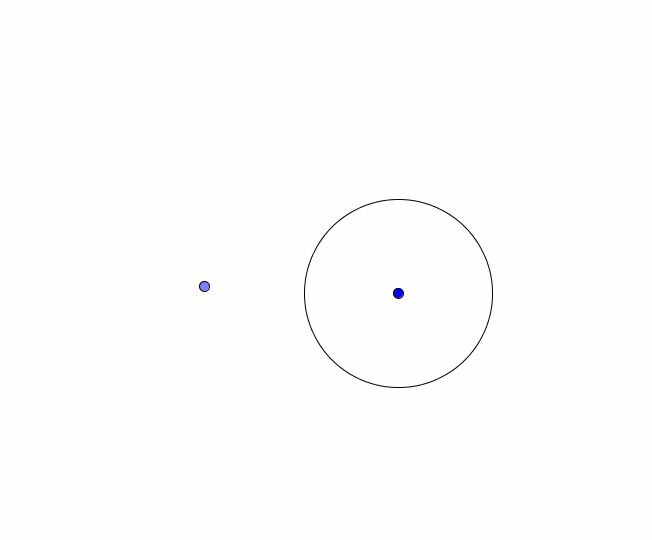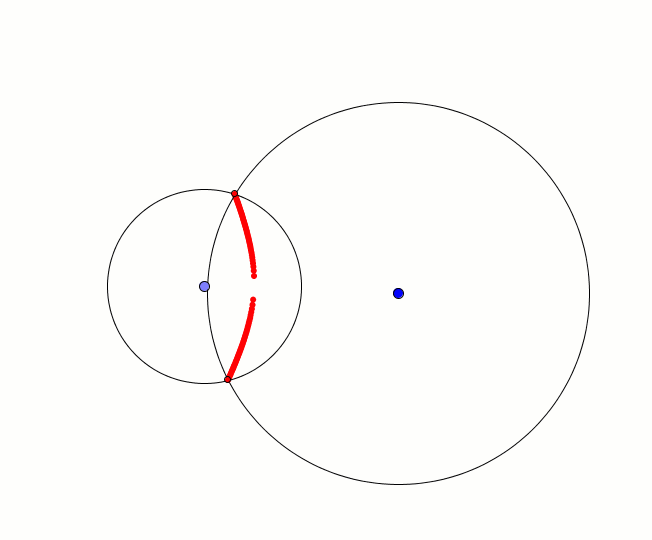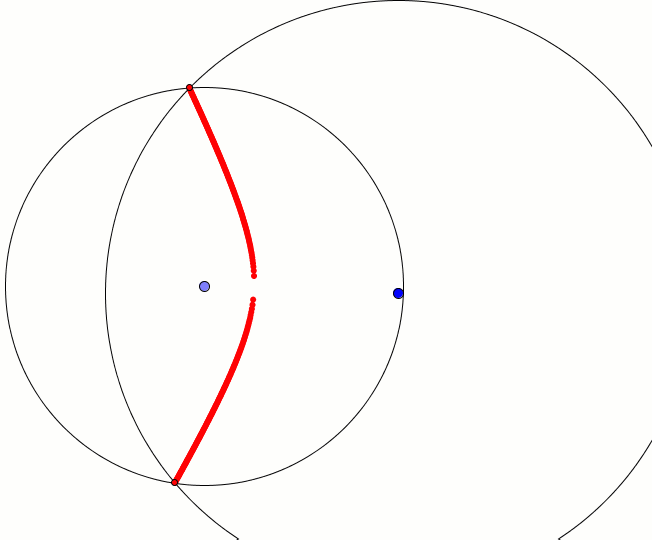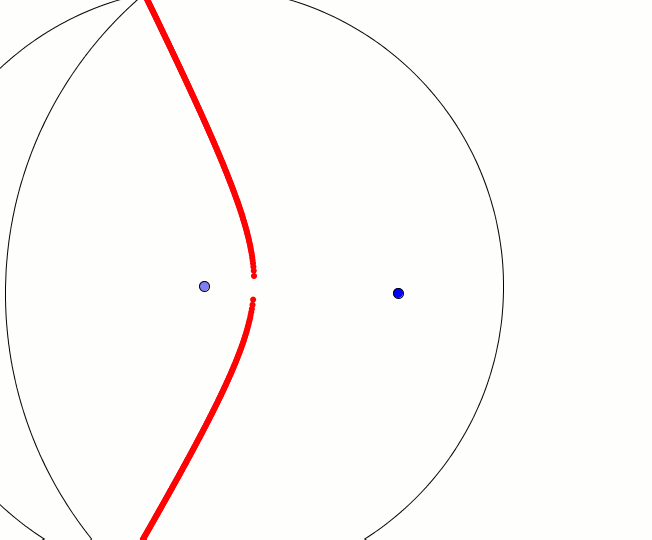
animacja pokazująca zakreślanie hiperboli przez miejsce przecięcia okregów — Zakreślanie ramienia hiperboli przez punkty wspólne dwóch okręgów o promieniach
r i r + a, a = const

hiperbola jako obwiednia prostych

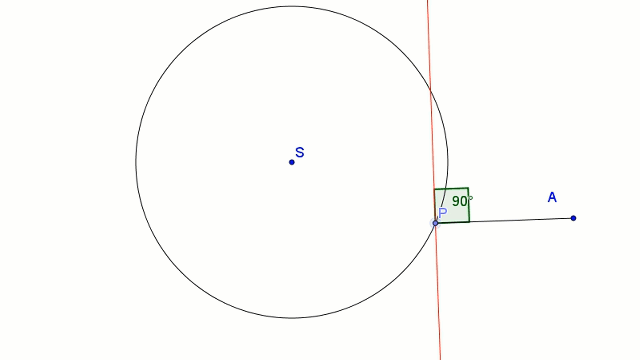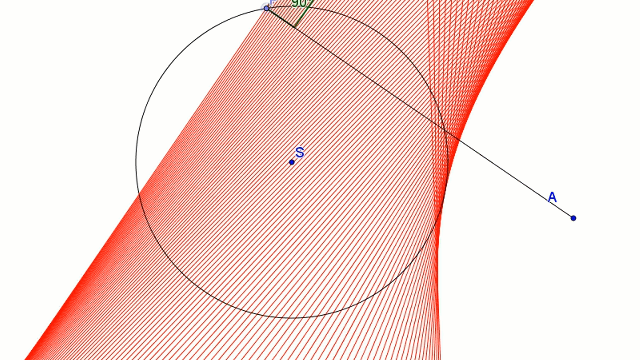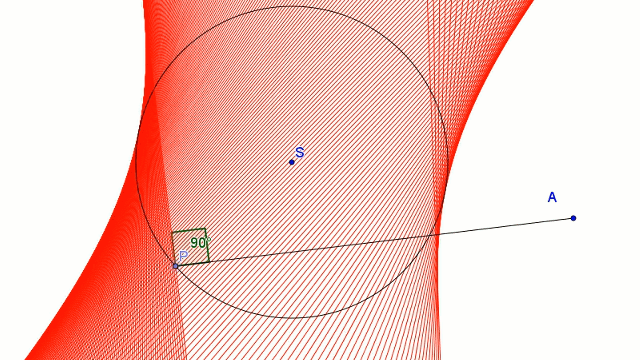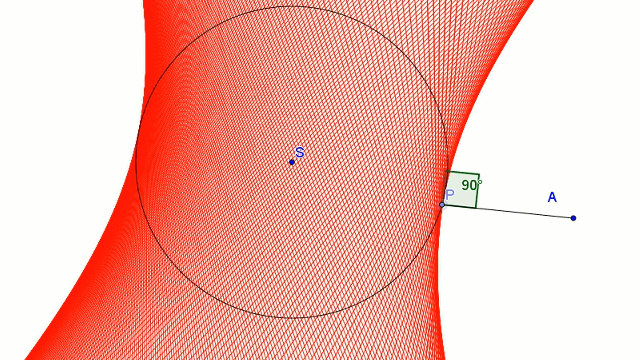
Mówimy, że krzywa jest obwiednią prostych (lub okręgów), jeśli dla każdego punktu tej krzywej istnieje jedna z prostych styczna w tym punkcie do krzywej. By uzyskać hiperbolę jako obwiednie prostych:

ustalamy punkt A poza kołem okręgu
wybieramy punkt P na okręgu,
tworzymy odcinek AP,
w punkcie P kreślimy prostą prostopadłą do odcinka AP

Prosta ta w trakcie poruszania punktem P tworzy hiperbolę - hiperbola ta jest obwiednią rodziny tych prostych

animacja pokazująca hiperbolę jako obwiednię prostych — Hiperbola jako obwiednia prostych

wykorzystanie hiperboli w ustalaniu położenia ruchomego obiektu

Radionawigacja hiperboliczna to rodzaj nawigacji wynaleziony podczas drugiej wojny światowej. Wykorzystuje ona system co najmniej 3 radiostacji pracujących w stałej synchronizacji. Opóźnienie jednego sygnału względem drugiego pozwala wyznaczyć różnicę odległości dzielącej nas od źródeł tych sygnałów. Wykorzystując zasady geometrii można wyznaczyć na tej podstawie hiperbolę, na której się znajdujemy. Tak samo dzieje się dla innej pary radiostacji i przecięcie dwóch hiperbol pozwala określić naszą pozycję.

Poniższa animacja pokazuje przybliżone działanie śledzenia położenia obiektu w systemie nawigacji hiperbolicznej.

animacja pokazująca przybliżoną symulację śledzenia położenia obiektu w systemie nawigacji hiperbolicznej — Przybliżona symulacja śledzenia położenia obiektu w systemie nawigacji hiperbolicznej