spis treści
stożkowe jako krzywe przecięcia stożka
Zanim zajmiemy się krzywymi przecięć powierzchni stożkowej płaszczyzną, czyli stożkowymi, opiszmy najpierw czym jest powierzchnia stożkowa, zwana dawniej konusem. Jest to bryła nieograniczona zamknięta, która powstaje jako zbiór wszystkich prostych, przechodzących przez ustalony punkt W (wierzchołek powierzchni stożkowej) i drugi punkt A, który porusza się po dowolnej krzywej płaskiej, nieprzechodzącej przez punkt W. Ponieważ prosta ta tworzy powierzchnię stożkową, nazywamy ją tworząca stożka. W zależności od rodzaju krzywej po której porusza się punkt A rozróżniamy: stożki eliptyczne, hiperboliczne, paraboliczne i inne... Poniższe animacje prezentują fragmenty wybranych powierzchni stożkowych.
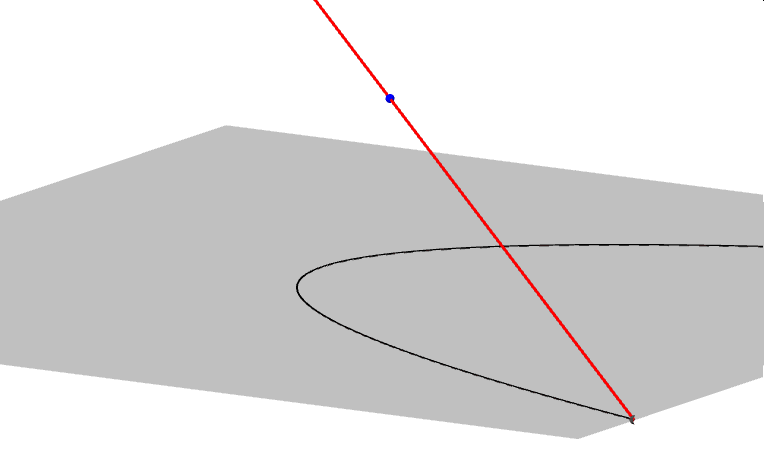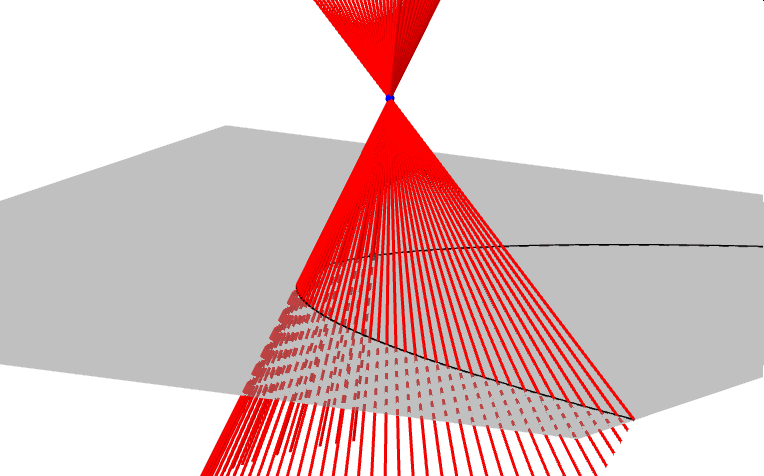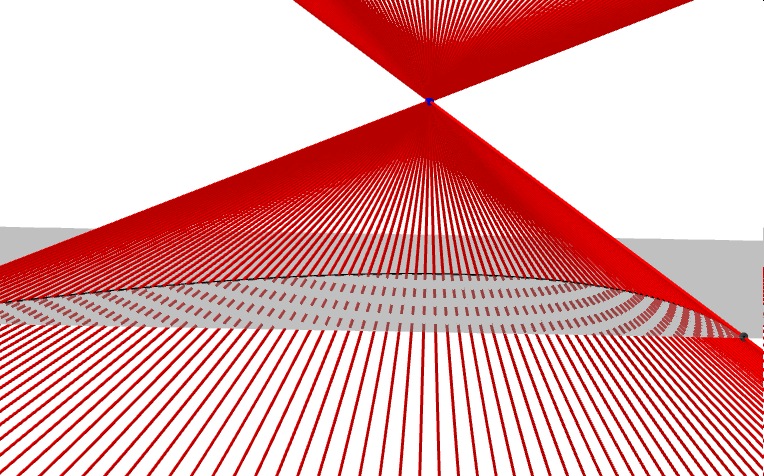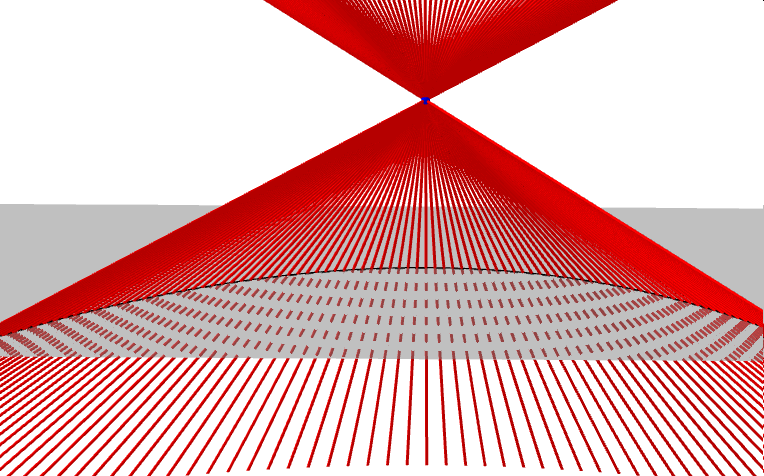
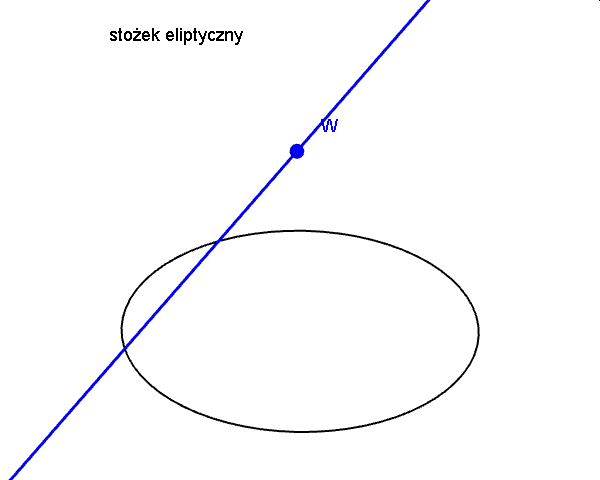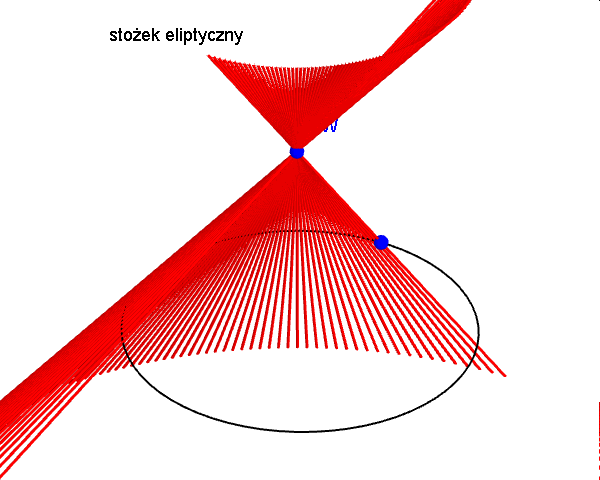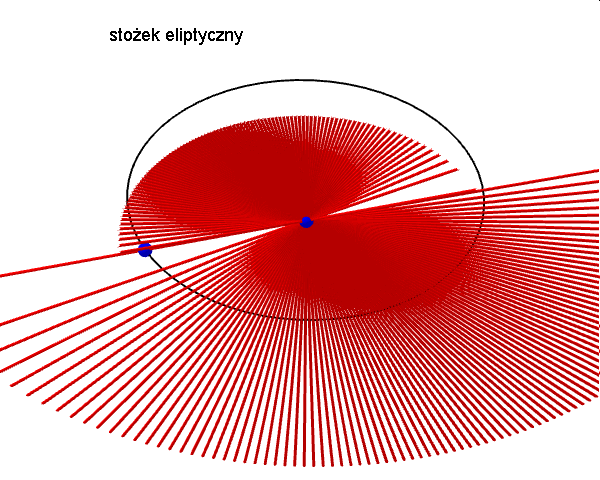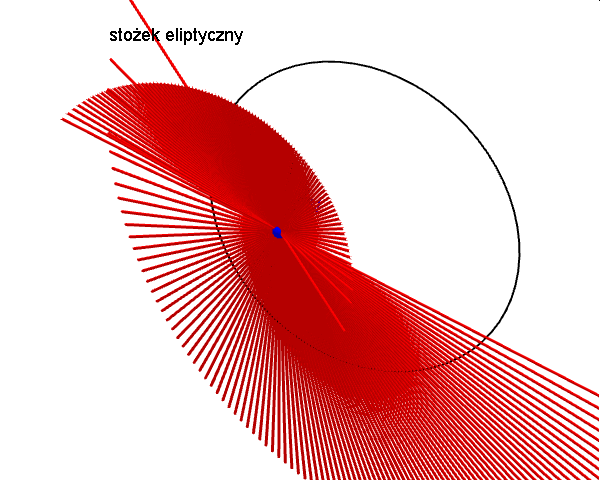
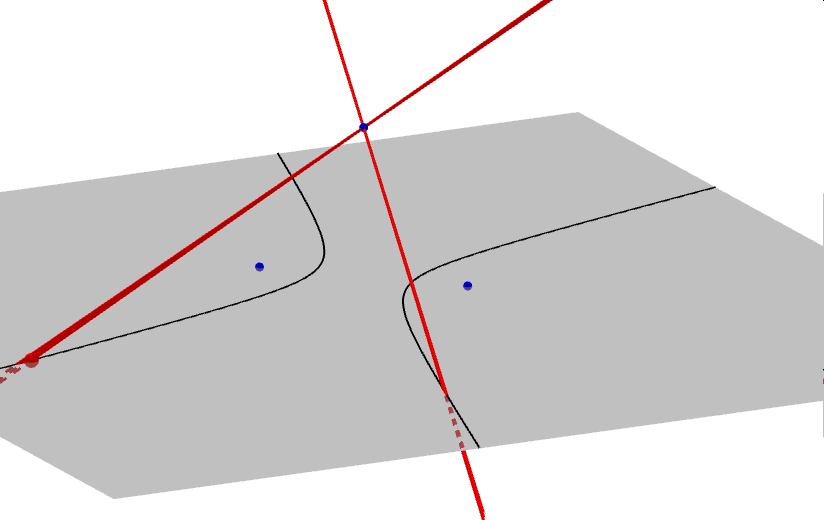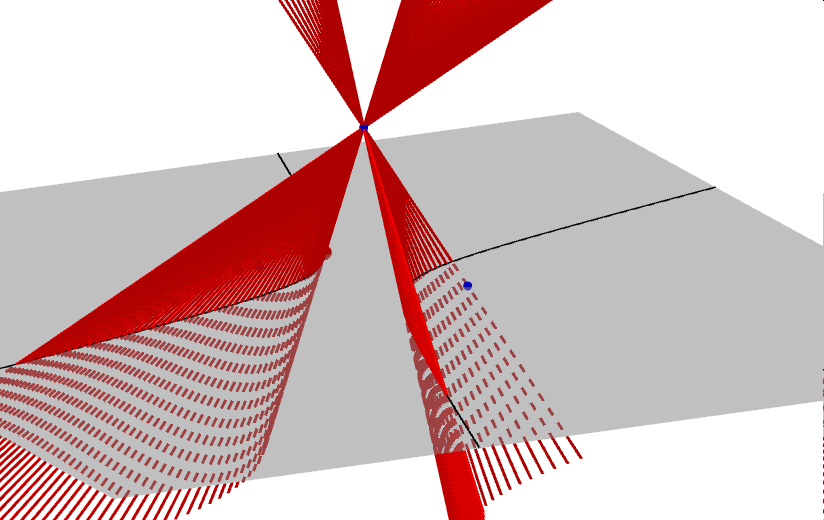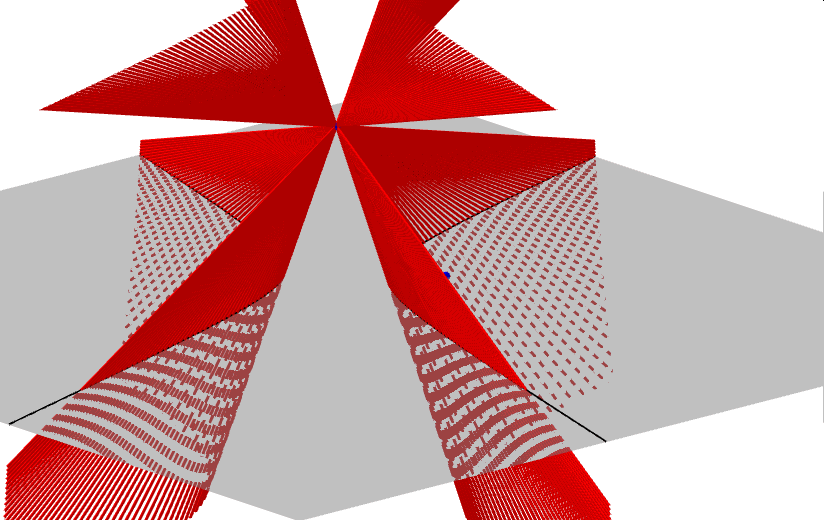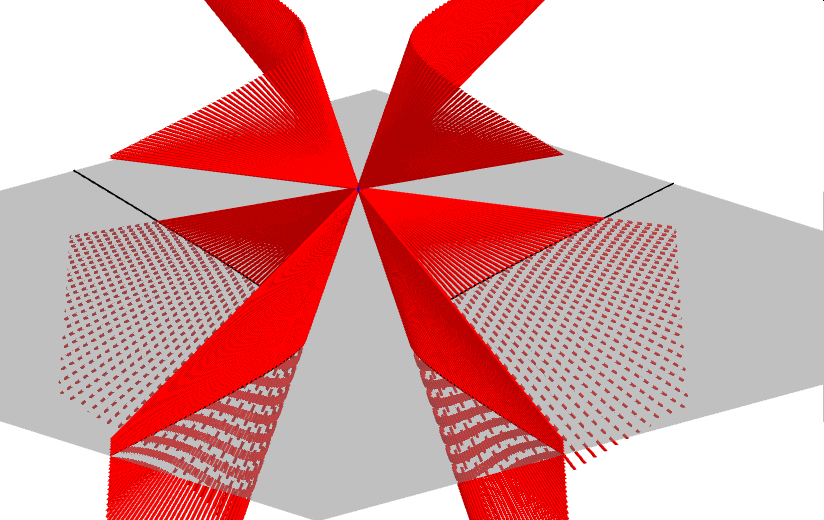
Zajmijmy się teraz tradycyjnym stożkiem, czyli powierzchnią stożkową zbudowaną na bazie koła. Krzywymi stożkowymi nazywamy zbiór punktów przecięcia tego stożka z płaszczyzną. W zależności od kąta, jaki tworzy płaszczyzna przekroju z osią stożka, uzyskujemy różne krzywe stożkowe.
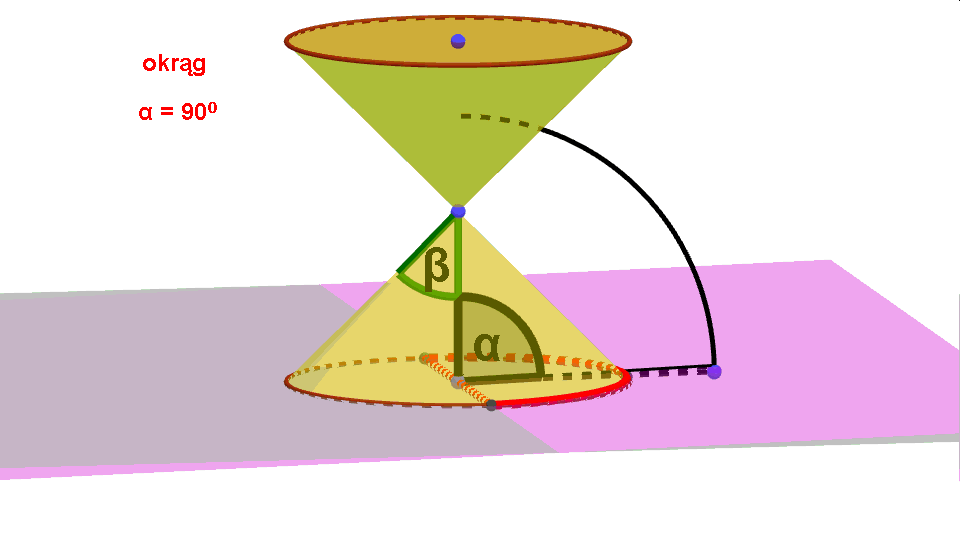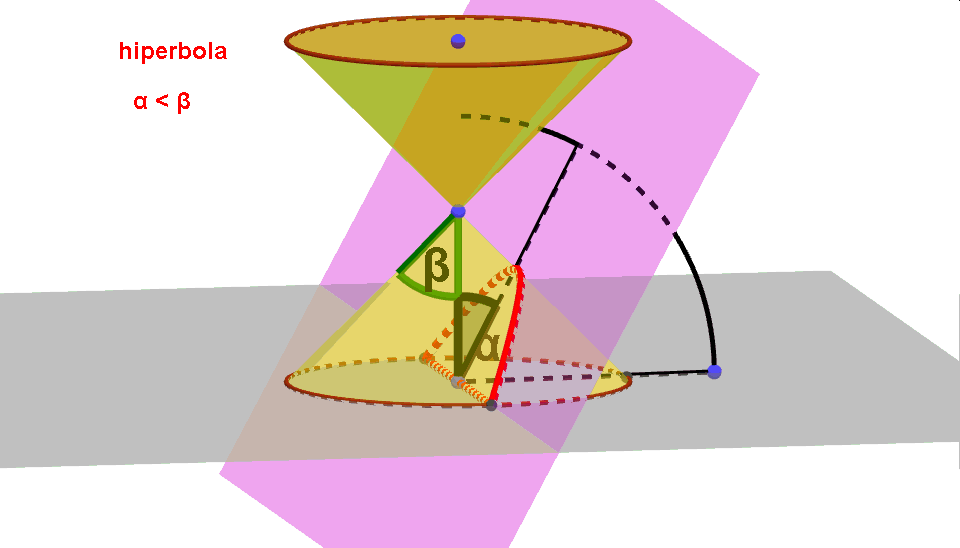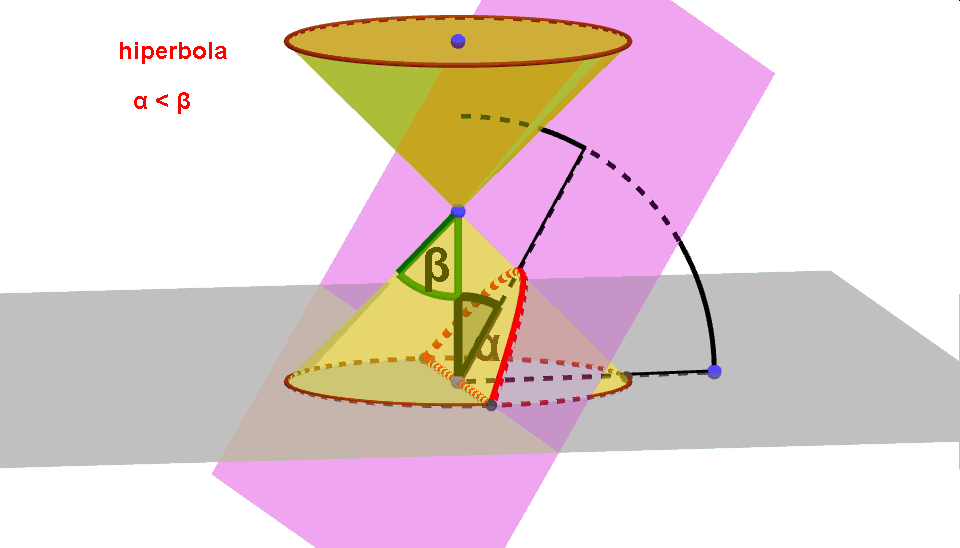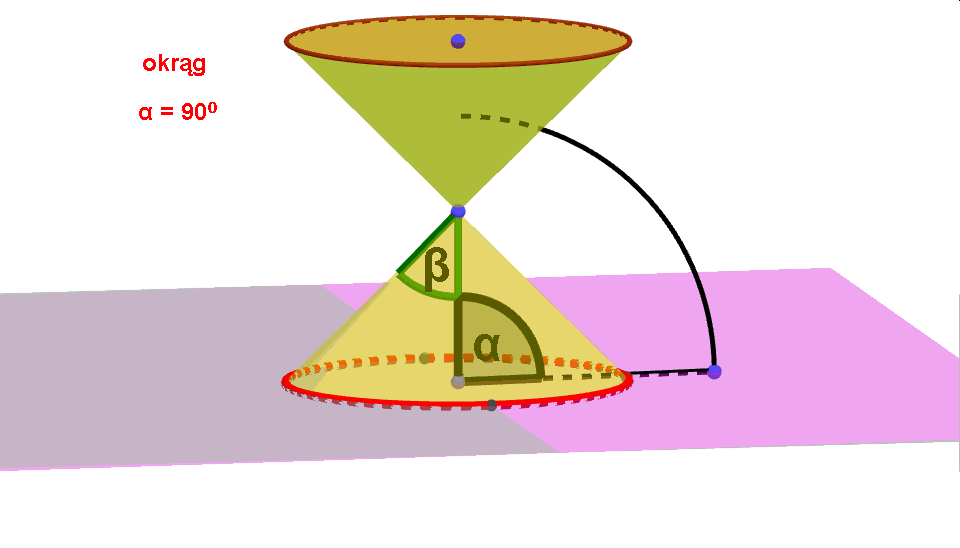
Przekrojem osiowym naszego stożka jest trójkąt. Niech β będzie kątem nachylenia tworzącej stożka do jego osi, zaś α kątem, jaki tworzy płaszczyzna przekroju z osią stożka. Przy zmianie miary kąta α uzyskamy różne rodzaje przekroju:
- Okrąg, gdy α = π2. Powierzchnia cięcia jest w tym wypadku równoległa do podstawy stożka.
- Elipsa, gdy β < α < π2.
- Parabola, gdy α = β. W tym przypadku powierzchnia cięcia jest równoległa do tworzącej stożka.
- Hiperbola 0 < α < β.
- Dwie proste przecinające się gdy α = 0°
stożkowe na płaszczyźnie
Stożkowe można potraktować również jako zbiór punktów P płaszczyzny takich, że stosunek odległości tych punktów od ognisk (ogniska) do odległości od kierownic (kierownicy) jest stały i nazywamy go mimośrodem ε.
- Dla elipsy: ε = |F1P||GP| = |F2P||PA| < 1
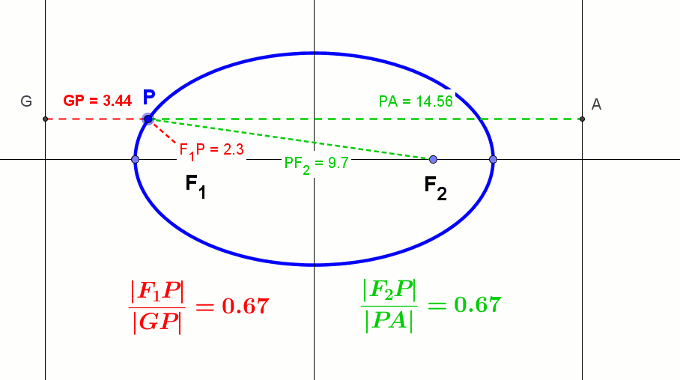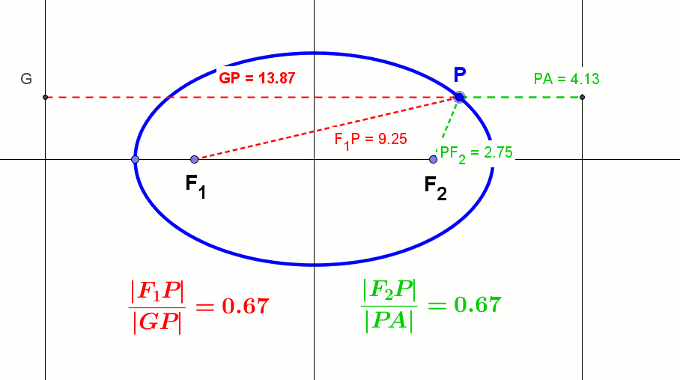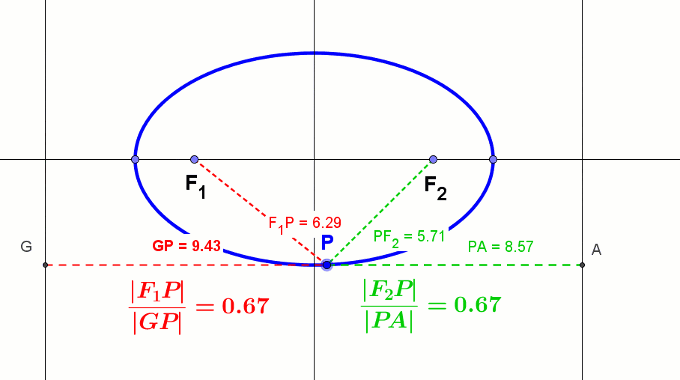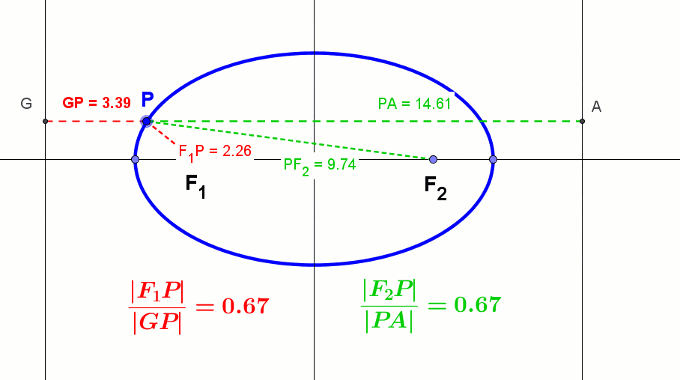
Animacja elipsy z kierownicami - Dla paraboli ε = |PF||PQ| = 1
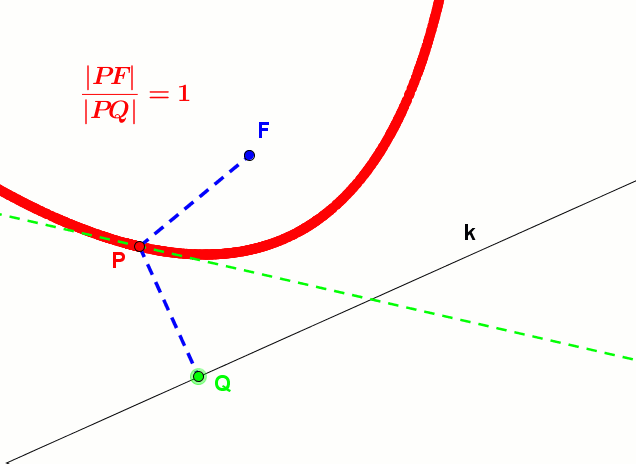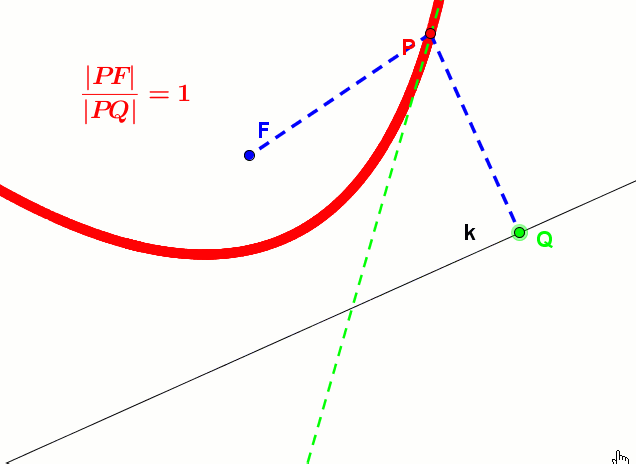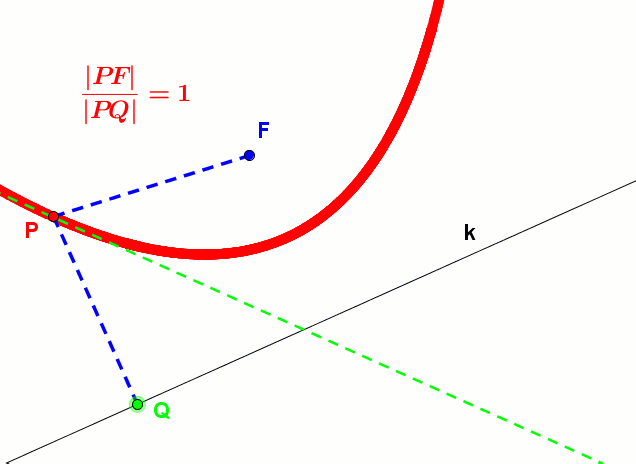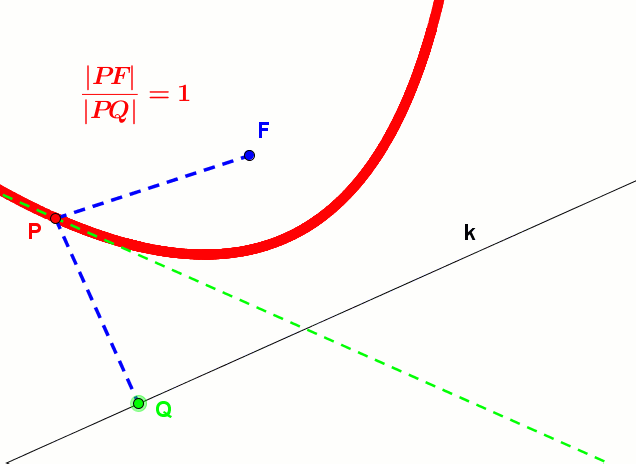
Animacja paraboli z kierownicą - Dla hiperboli ε = |PF2||PK| > 1. Podobnie dzieje się dla drugiego ogniska i kierownicy.
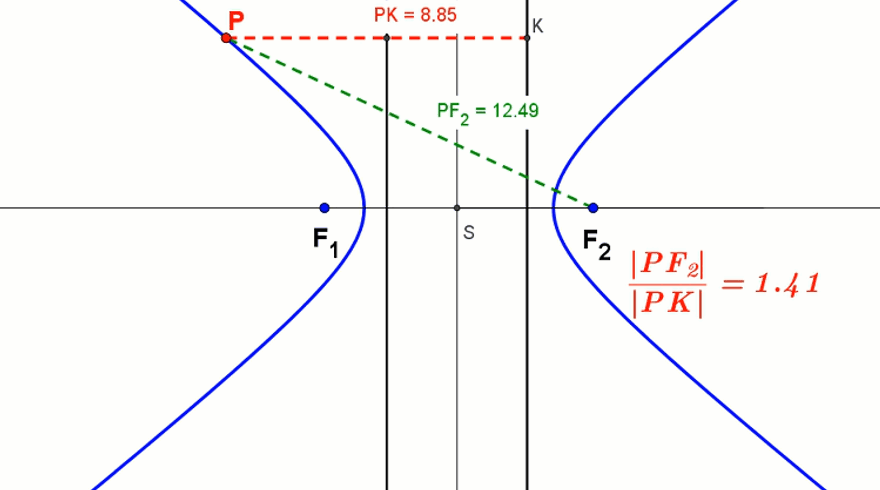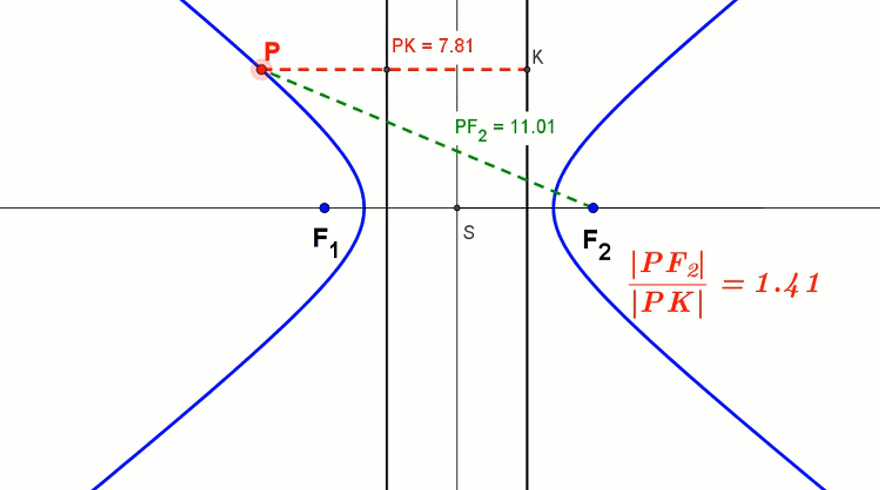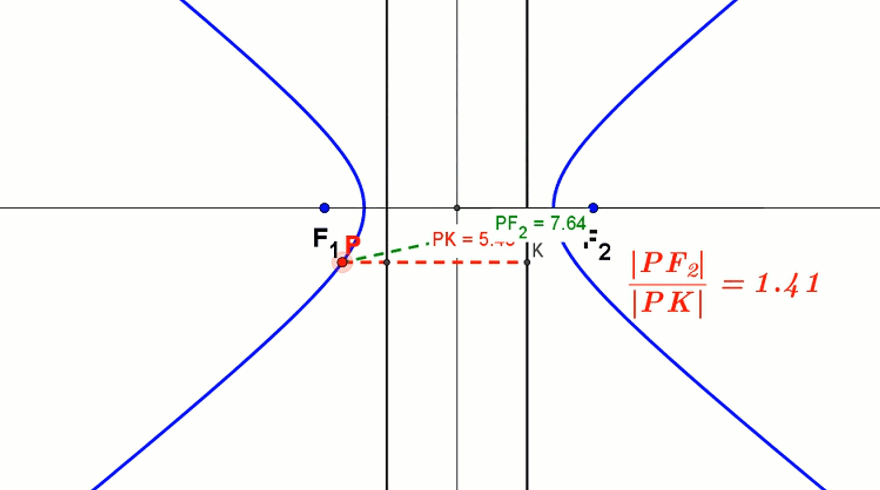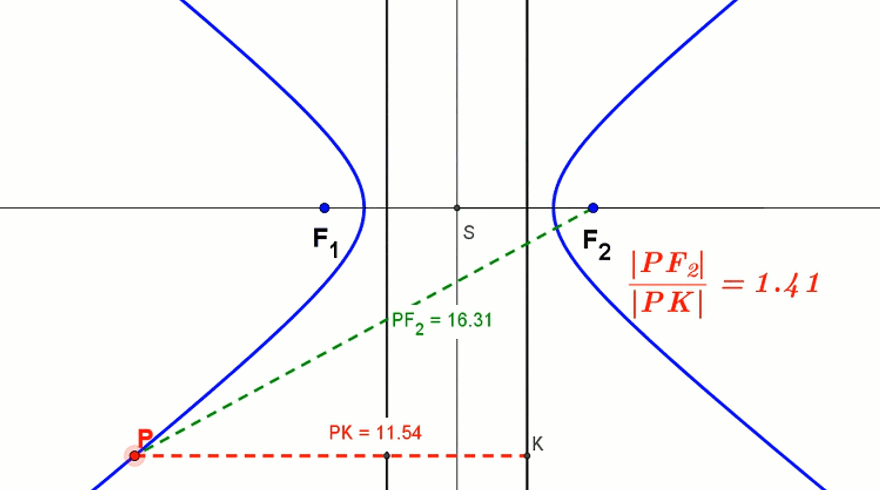
Animacja hiperboli z kierownicami
stożkowe w układzie współrzędnych
Każdą krzywą stożkową możemy wyrazić za pomocą równania drugiego stopnia względem zmiennych x oraz y w kartezjańskim układzie współrzędnych: ax2 + by2 + cxy + dx + ey + f = 0
W zależności od współczynników a, b, c, d, e i f stożkowa jest kołem, elipsą, parabolą, hiperbolą, dwiema prostymi lub punktem. Ponieważ w równaniu tym występuje 5 współczynników, w wielu programach komputerowych, takich jak GeoGebra czy Cabri, można wykreślić stożkową wskazując pięć punktów. Można powiedzieć, iż 5 punktów jednoznacznie określa rodzaj stożkowej.
spojrzenie na historię
Za twórcę teorii krzywych uznaje się Menaichmosa, greckiego matematyka. Stożkowe odkrył podczas próby rozwiązania problemu delijskiego. Inny Grek Apoloniusz z Pergi wprowadził znane nam dzisiaj pojęcia elipsy, paraboli i hiperboli.

(ok. 260r.p.n.e - 190r.p.n.e)
Przez wieki uznawano krzywe stożkowe za niepotrzebne i nie widziano dla nich zastosowania, wartości nabrały dopiero w XVII w. przy okazji odkryć Johannesa Keplera.

(1571 - 1630)
W XIX w. stożkowymi zainteresowani byli francuscy uczeni tacy jak Germinal Pierre Dandelin, o którym jeszcze usłyszymy oraz Jean Victor Poncelet.

(1794 - 1847)