MATEMATYKA ZAPOMNIANYCH MISTRZÓW

Jednym z najbardziej znanych i rozpowszechnionych twierdzeń jest twierdzenie japońskie.Mówi ono, że niezależnie od triangulacji wielokąta wpisanego w okrąg, suma promieni okręgów wpisanych w powstałe trójkąty jest stała.

Niech wypukły cykliczny wielokąt zostanie triangulowany w dowolny sposób.Narysujmy okręgi wpisane w powstałe trójkąty. Wtedy suma promieni okręgów wpisanych jest stała niezależnie od wybranej triangulacji. Twierdzenie to można udowodnić za pomocą twierdzenia Carnota, czyli twierdzenia cosinusów. Promienie okręgów wpisanych na rysunku powyżej wynoszą odpowiednio 0.623, 0.371,0.606, 0.402, a promienie okręgów wpisanych w triangulacji na rysunku obok wynoszą 0.777, 0.733,0.236, 0.256, dając w sumie 2.002 w każdym przypadku. Odwrotność jest również prawdą: jeśli suma promieni okręgów wpisanych nie zależy od triangulacji wielokąta, to wielokąt jest cykliczny.

Kolejnym ciekawym zagadnieniem jest prooblem Katayamahiko. Niech będzie dany okrąg o promieniu r zawierający trzy koła o promieniu t, wtedy połączone środki okręgów tworzą trójkąt równoboczny o boku 2 t. Znajdź t w zakresie r, jeśli r=10.

Rozwiązanie

Znamy odległość od środka okręgu opisanego na pozostałych trzech kołach, do każdego z wierzchołków trójkąta równobocznego. Wiedząc, że utworzony trójkąt jest równoboczny i korzystając z własności cosinusów, możemy zauważyć, że

Problem Sawy Masayoshi'ego został sformułowany na zasadzie wyzwania.Treść brzmiała następująco: Elipsa jest wpisana w trójkąt prostokątny z jej główną osią równolegle do przeciwprostokątnej trójkąta. W elipsie są wpisane dwa koła o promieniu r. Trzecie koło o promieniu r styka się z elipsą oraz przyprostokątnymi-a i b. Znajdź zależność pomiędzy promieniem r, a bokami a i b trójkąta.

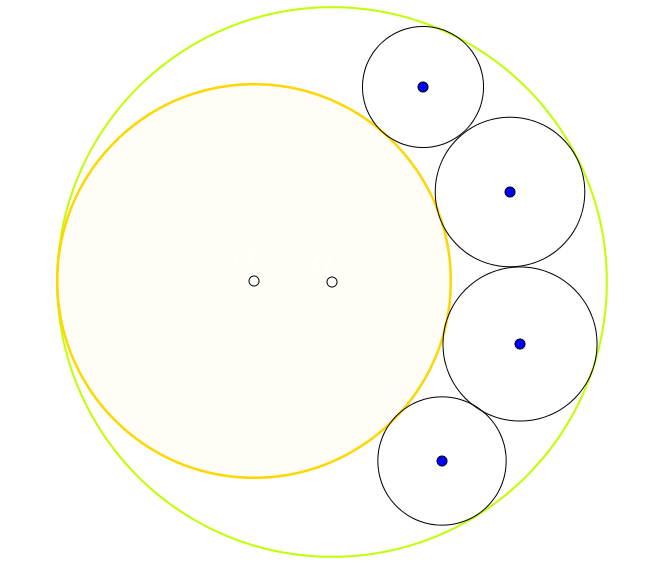
Wspomniany problem sangaku jest kolejnym prostym zagadnieniem, który dotyczy okręgów wpisanych. Jest ono częścią kolekcji Fukagawy i Pedoe, którzy nie znaleźli go na tabliczce, ale w książce z 1810 roku. Brzmi ono:"Koło ze środkiem w punkcie O' i promieniu r' jest wewnętrznie styczne z okręgiem o środku w punkcie O i promieniu r, a łańcuch okręgów kontaktowych o środkach w punktach O_i i promieniach r_i, gdzie i = 1, 2, 3, 4, jest wpisany w wycinek o kształcie księżyca utworzoną przez okrąg o środku w punkcie O i promieniu r i okrąg o środku w punkcie O' i promieniu r'. Wykaż, że

Sangaku można łatwo rozwiązać za pomocą ogólnej formuły:

gdzie koła w łańcuchu, styczne do siebie odpowiadają wartościom t różnym od 1! Używając A = rr' i B = r - r', możemy stwierdzić, że

Podstawiając w

Sprawdźmy prawdziwość: 1 + 3 · 3² = 3 · 2² + 4² równanie jest prawdziwe, tak więc problem zostaje rozwiązany.