Algorytmy liczb pierwszych
Sprawdzenie pierwszości poprzez sprawdzenie podzielności
Najprostszą metodą aby zbadać czy liczba jest pierwsza jest sprawdzenie jej dzielników. Aby zbadać liczbę n sprawdzamy kolejne liczby naturalne należące do przedziału [2,..., √n].
Jeżeli okazało by się, że któraś z tych liczb jest dzielnikiem naszej liczby n, oznacza to, że nasza liczba nie jest pierwsza.
Jednak teraz pojawia się pytanie dlaczego wystarczy sprawdzić tylko liczby od 2 do √n
Przenalizujmy to na przykładzie liczb: 23, 33 i 36.
√23 ≈ 4,8
D23 = {1, |4,8|, 23}
√33 ≈ 5,7
D33 = {1, 3, |5,7|, 11, 33}
√36 = 6
D36 = {1, 2, 3, 4, 6, 9, 12, 18, 36}
Można łatwo zauważyć, że liczba n ma tyle samo dzielników większych √n jak i mniejszych od √n. Dzięki tym przykładom można zauważyć, że jeśli jedynym dzielnikiem mniejszym lub równym √n jest 1 to liczba ta jest pierwsza.
Powyższą metodą można sprawdzić pierwszość każdej liczby naturalnej większej od 1, jednak w porównaniu do testu Lucasa-Lehmera czas wykonania tego algorytmu dla bardzo dużych liczb jest dłuższy.
Poniżej można wpisać dowolną liczbę i sprawdzić to czy jest pierwsza oraz to jak działa ten algorytm.
(Dla n < 1 000 000, wyświetlany jest cały algorytm, a w przypadku n ≥ 1 000 000 wyświetlany jest tylko wynik działania algorytmu oraz czas jego działania.).
Sito Eratostenesa
Sito Eratostenesa jest to algorytm przypisywany Eratostenesowi z Cyreny wymyślony już w III w. p.n.e. służący do wyznaczania liczb pierwszych z zadanego przedziału [2;n].
Działanie sita polega na wybraniu ze zbioru [2;n] najmniejszej liczby czyli 2 i wykreśleniu wszystkich jej wielokrotności większej od niej, czyli 4,6,8,10,.....
Z pozostałych liczb wybieramy kolejną najmniejszą nie wykreśloną czyli 3 i ponownie wykreślamy wszystkie jej wielokrotności czyli: 6,9,12,15,..... Niektóre liczby takie jak 6 lub 12 będą skreślone jeszcze raz czym się nie przejmujemy.
Tak samo robimy z kolejną najmniejszą niewykreśloną liczbą czyli 5.
Proces powtarzamy tak długo, gdy liczba i, której wielokrotności chcemy wykreślać jest większa od √n.
Dla danej liczby n wszystkie wykreślonej liczby mniejsze lub równe n są liczbami pierwszymi.
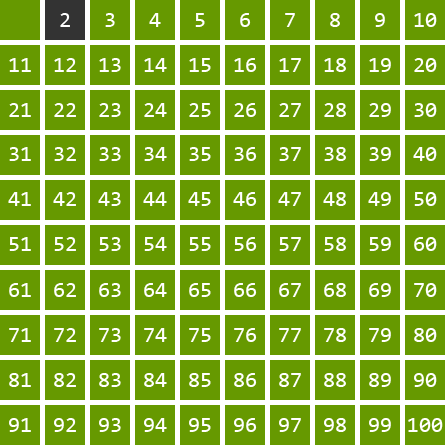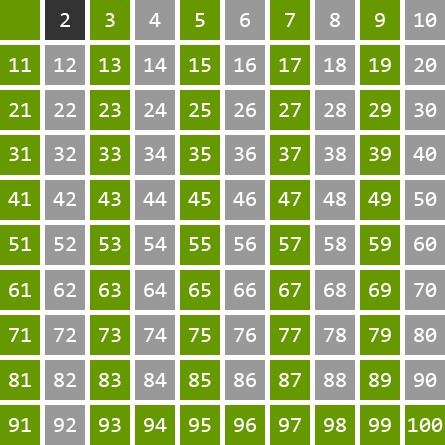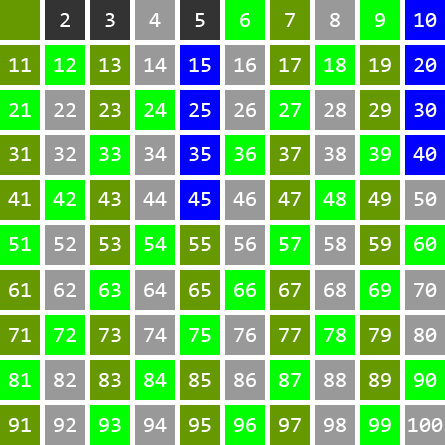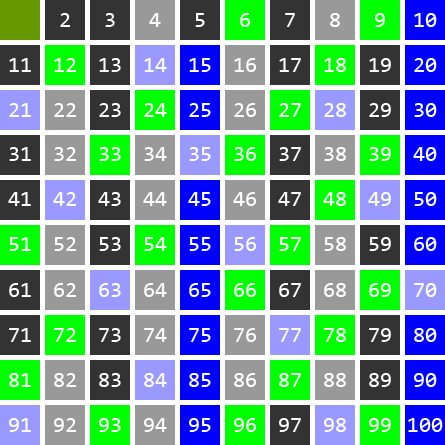
Autor animacji - mgr inż. Adrian Zapała
Poniżej można wpisać dowolną liczbę n, dla której sito znajdzie wszystkie liczby pierwsze mniejsze lub równe n

Test Lucasa-Lehmera
Test Lucasa-Lehmera jest testem pierwszości dla liczb Mersenne'a. Test ten został ułożony przez Edwarda Lucasa w 1856, a następnie ulepszony przez niego w 1878. Podany wniosek stwierdzał, że liczba 2p-1 jest liczbą pierwszą wtedy gdy jest dzielnikiem liczby wyrazu Lp-1 ciągu określonego następująco:
L1=4
Ln= Ln-12-2
Nie wiadomo, jak Lucas wymyślił tę własność. Nie potrafił jej również w żaden sposób udowodnić.
Warunek podany przez Lucasa został udowodniony dopiero w XX wieku przez Amerykanina Derricka Henry'ego Lehmera i od tego czasu nosił nazwą testu Lucasa-Lehmera.
Ten właśnie test jest wykorzystywany przez serwis GIMPS do znajdowania dużych liczb pierwszych Mersenne’a.
Zaletą tego algorytmu są takie, że działa bardzo szybko i dla przykłady liczbę 289-1 posiadającą 27 cyfr potrafi określić jako liczbę pierwszą w ciągu 1ms!
Jego główną wadą jest fakt, że używać można go tylko dla liczb Mersenne’a.
Poniżej można sprawdzić działanie testu Lucasa-Lehmera. Poniżej można wprowadzić liczbę n, która będzie n-tą liczbą Mersenne’a i sprawdzić działanie testu oraz czy ta liczba jest pierwsza.
(Dla n < 70, wyświetlany jest cały algorytm, a w przypadku n ≥ 70 wyświetlany jest tylko wynik działania algorytmu oraz czas jego działania).

