Zastosowania
RSA
W 1977 roku trzej profesorowie z MIT (Massachusetts Institute of Technology) w USA, Ronald Rivest, Adi Shamir i Leonard Adleman opublikowali nowy rodzaj szyfrowania, którego nazwano od pierwszych liter ich nazwisk RSA. Algorytm RSA jest aktualnie jednym z najpopularniejszych asymetrycznych algorytmów kryptograficznych. Jego zastosowanie można znaleźć w szyfrowaniu wiadomości, w operacjach między bankami oraz w komunikatorach internetowych.
W tym momencie warto wyjaśnić czym różni się symetryczny system szyfrowania od niesymetrycznego. Symetryczny system szyfrowania to taki, w którym klucz szyfrujący pozwala zarówno szyfrować dane, jak również odszyfrowywać je. Jego wadą jest to, że konieczne jest ścisłe chronienie kluczy. Niesymetryczny algorytm jakim jest algorytm RSA charakteryzuje się tym, że występują w nim dwa klucze: publiczny, który umożliwia jedynie zaszyfrowanie danych i w żaden sposób nie ułatwia ich odczytanie dzięki czemu nie musi być chroniony. Drugim kluczem jest klucz prywatny, który służy jedynie do odczytywania informacji zakodowanych przy pomocy publicznego klucza. Klucz ten jednak musi być ściśle chroniony, ponieważ jego znajomość umożliwiłaby odczytanie zaszyfrowanej wiadomości.
Całym algorytm RSA można podzielić na kilka części:
- Wygenerowanie klucza publicznego oraz prywatnego.
- Zaszyfrowanie danych przy użyciu klucza publicznego oraz wysłanie zaszyfrowanych danych do adresata.
- Deszyfracja wiadomości za pomocą klucza prywatnego przez odbiorcę.
Tworzenie klucza RSA
| p = 19 q = 17 |
Wybranie dwóch dowolnych liczb pierwszych. Dla przykładu będę korzystać z małych liczb pierwszych, aby ułatwić obliczenia. W rzeczywistości dla klucza 2048-bitowego, który jest aktualnie wykorzystywany, liczby te są rzędu 22048 |
| Ø = 288 | Obliczamy funkcję Eulera Ø = (p - 1) * (q - 1): Ø = (19 - 1) * (17 - 1) = 18 * 16 = 288 |
| n = 323 | Obliczamy moduł n = p * q: n = 19 * 17 = 323 |
| e = 35 | Wyznaczamy wykładnik publiczny e, który jest względnie pierwszy wraz z Ø. Oznacza to, że NWD(e,Ø) powinno być 1. Liczba ta nie musi być pierwsza. Dla naszego Ø = 288, przykładem liczby spełniającej ten warunek jest e = 35 |
| d = 107 | Teraz wyznaczamy wykładnik prywatny, który ma być odwrotnością modulo Ø liczby e co oznacza, że d * 35 mod 288 = 1 Liczbą spełniającą ten warunek jest 107 |
| klucz publiczny [35, 323] | Naszym kluczem publicznym są liczby: [e, n] |
| klucz prywatny [107, 323] | Naszym kluczem prywatnym są liczby: [d, n] |
Szyfrowanie danych przy użyciu klucza publicznego
| e = 35 n = 323 |
Do zaszyfrowania użyjemy klucza publicznego w postaci liczb e i n, który zostaje wysłany przez adresata |
| t = 36 | Aby zaszyfrować wiadomość należy zamienić znaki na liczby naturalne t. Liczby te muszą spełniać nierówność 0 < t < n. Osoba do której wysyłamy tę wiadomość musi również znać nasz sposób kodowania. Tym zajmują się oprogramowania które szyfrują i deszyfrują wiadomości, które posiada odbiorca i nadawca. Dla przykładu zaszyfrujmy literę b do której przypiszemy liczbę 36. |
| c = 161 | Następnym krokiem jest wyznaczenie liczby c ze wzoru c = te mod n c = 3635 mod 323 = 161 |
Deszyfracja danych przy użyciu klucza prywatnego
| c = 161 d = 107 n = 323 |
Od adresata otrzymujemy zaszyfrowaną wiadomość c, oraz klucz prywatny w postaci liczb d i n |
| t = 36 | Następnie należy wykonać operacje t = cd mod n, aby zdeszyfrować wiadomość t = 161107 mod 323 = 36 |
| 36 → b | Dzięki tej operacji oraz znając sposób kodowania przez adresata zamieniamy 36 na b |
W 2009 roku grupie naukowców udało się złamać klucz o długości 768 bitów co trwało aż 2 lata, a wynik pracy algorytmów deszyfrujących zajął aż 5 TB danych! Aktualnie standardem jest klucz 2048 bitowy. Cała siła tego algorytmu tkwi w matematycznym problemie znalezienia dwóch podzielników dużej liczby, które po przemnożeniu dają w wyniku tę bardzo dużą liczbę. Dla komputerów mnożenie jest procesem szybkim, ale dzielenie już nie.
Najsłabszym ogniwem algorytmu RSA jest konieczność ochrony klucza prywatnego. Nie ważne jak bardzo matematycznie będzie skomplikowany klucz prywatny, jeżeli hackerowi uda się uzyskać do niego dostęp przy pomocy przejęcia kontroli nad serwerem to będzie w stanie przejąć i bez problemu odszyfrować zaszyfrowaną wiadomość. Jednak przy odpowiednich zabezpieczeniu wysłania klucza prywatnego rozszyfrowanie jest praktycznie niemożliwe. Całe bezpieczeństwo tego algorytmu opiera się na czasie. Współczesne szyfry kryptograficzne są tworzone w taki sposób, aby ich deszyfracja trwało nieskończenie długo i na tym polega siła. I tutaj pojawiają się komputery kwantowe.
Komputery kwantowe są dużo szybsze niż domowe komputery, a nawet serwery. Jak bardzo? Normalnemu komputerowi łamanie klucza 1024-bitowego zajęłoby około 1.5 miliona lat, ale temu samemu komputerowi złamanie klucza o długości 2048-bitów zajęłoby 4 miliardy razy dłużej. Aby uzmysłowić sobie jak długo by to trwało to licząc, że wszechświat ma ok. 13,7 miliardów lat, złamanie tego szyfru trwało by 500 000 razy dłużej! Jednakże czy komputery kwantowe są na tyle szybkie aby zagrozić szyfrowi RSA-2048? W 2015 roku eksperci oszacowali, że komputer kwantowy będzie potrzebował miliarda kubitów, aby złamać szyfrowanie oparte o RSA-2048 w 8 godzin! Aktualnie nowoczesne komputery kwantowe posiadają ok. 50-80 kubitów, jednakże przy obecnym tempie rozwoju technologicznego może minąć kilkanaście lub nawet kilka lata aby szyfr RSA-2048 nie był już bezpieczny.
Aktualnie szyfrowania 2048-bitowego używa się w bankowości online, komunikatorach internetowych, szyfrowaniu poczty lub plików. Przy złamaniu tego szyfru wszystkie transakcje bankowe będą możliwe do odszyfrowania. Jednakże rozwiązanie tego problemu jest bardzo proste, gdyż zwiększnie klucza z 2048-bitowego do 4096-bitowego będzie już niemożliwe do rozszyfrowania w rozsądnym czasie nawet dla nowoczesnych komputerów kwantowych.
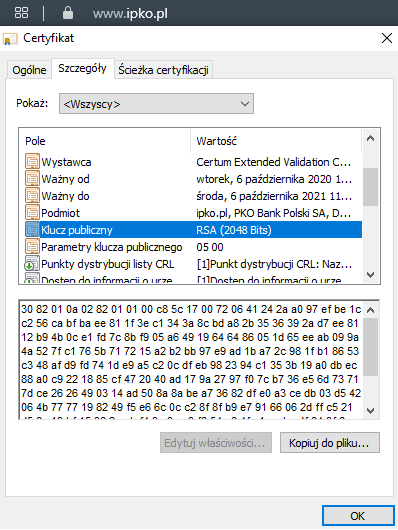
Dla osób zaciekawionych tematem, możliwe jest sprawdzenie z jakiego klucza publicznego oraz z jakiego zabezpieczenia korzysta twój bank. Dla przykład bank PKO korzysta z wersji 2048-bitowej klucza publicznego RSA.