Na podstronie o naturze omówiliśmy już historię dotycząca odnajdywania złotej proporcji w ciele człowieka. Tamte fakty są bezpośrednią przyczyną pojawienia się liczby $\varphi$ w sztuce.
Zacznijmy od człowieka witruwiańskiego Leonarda da Vinci. Powinniście już wiedzieć, że proporcje tam użyte miały stanowić kanon piękna. Przez wiele lat był on używany w sztuce i architekturze. Jak już wcześniej wspominaliśmy istnieje przekonanie, że Leonardo da Vinci interesował się złotym podziałem. Dlatego też różni estetycy starali się znaleźć zastosowanie dla niego w kanonie piękna. Nasiliło się to po wydaniu „De Divina Proportione” Luca Paciolego. Błędna interpretacja tego dzieła przyczyniła się do zwiększenia ilości prac opierających się na złotych proporcjach. Pacioli w swojej księdze rzekomo doradzał użycia złotego podziału w celu uzyskania pięknych harmonijnych proporcji. Niektórzy artyści błędnie połączyli tą interpretacje z rolą da Vinciego jako ilustratora księgi i wzięli sobie do serca liczbę $\varphi$. Tak zaczęły się tworzyć ugrupowania artystów stosujących „nowy kanon piękna” oraz estetyków usilnie szukających $\varphi$ gdziekolwiek się da.

Istnieją artyści, do których mamy pewność, że użyli w swoich dziełach złotej proporcji. Przykładem takiego artysty jest Salvador Dali. Przyjrzyjmy się jego obrazom: „Sakrament Ostatniej Wieczerzy” i „Atomowa Leda”.

Z prawej stronie znajduje się wcześniej wykonany przez artystę szkic „Atomowej Ledy”. Widać, że rysunek jest oparty na pentagonie. Jak wiemy tam gdzie są pięciokąty foremne tam też jest złoty podział. W tle dzieła „Sakrament Ostatniej Wieczerzy” możemy dostrzec dodekaedr.
Co więcej stosunek wymiarów tego obrazu odpowiada złotemu podziałowi. $\frac{267cm}{166.7cm} \approx 1.60$. Podobno sam Dali uważał, że każde dzieło sztuki musi być oparte na kompozycji i obliczeniach.

Innym dobrym przykładem jest „Section d'Or”. Jest to ugrupowanie artystyczne założone w październiku 1912 przez kubistów zafascynowanych proporcją i rozmieszczeniem form geometrycznych w sztuce. Niestety jedynie ich nazwa nawiązuje do złotej sekcji. Obecne toczą się debaty czy artyści z tego ugrupowania rzeczywiście wykorzystywali w swoich dziełach złota proporcję. Jedynie stosunek wymiarów (nietypowych jak na tamte czasy) niektórych obrazów, są bliskie liczbie $\varphi$. Przykładem jest „Les Baigneuses Albert'a” Gleizes: $\frac{171cm}{105cm} \approx 1.628$

Jednak szukanie złotego podziału poprzez obliczanie stosunku wymiarów obrazu nie jest dobrą metodą, ani żadnym dowodem. Najczęściej są to dosyć niedokładne przybliżenia $\varphi$.

Często mówi się, że Leonardo da Vinci używał złotej proporcji w swoich dziełach. Powodem tego jest m.in. jego powiązanie z Luca'ą Paciolim. Jednak sam artysta nigdy tego nie potwierdził. Znaczenie złotego podziału w „Człowieku Witurwiańskim” już zdementowaliśmy przy okazji omawiania człowieka. Jednak na wielu stronach internetowych poruszany jest również temat użycia „boskiego cięcia” w „Mona Lisie” i "Ostatniej Wieczerzy" Na stronie Muzeum Nauki w Bostonie, które powinno być wiarygodnym źródłem informacji, widnieją m.in. takie zdjęcie.

Może się nasunąć kilka pytań. Po pierwsze dlaczego złote prostokąty narysowano akurat w tych miejscach? Czy środek obrazu rzeczywiście jest w okolicach dekoltu damy? Dlaczego linie fioletowego prostokąta są różnej grubości? Poprzez zmianę grubości linii możemy dopasować prostokąty do wszystkiego. Nie istnieje dowód na to, że w tych obrazach został użyty złoty podział.

Piramidy egipskie od zawsze stanowiły jedną z największych zagadek ludzkości. Są źródłem wielu spekulacji. Różni pseudo, ale i prawdziwi, badacze doszukują się w tych budowlach matematycznego piękna, astronomicznego związku z naturą, przepowiedni przyszłości... Przypisują im mistyczne właściwości. Jednym z przedmiotów tychże spekulacji jest obecność złotego podziału u starożytnych Egipcjan. Przedstawimy tu sobie pobieżnie tylko kilka teorii związanych z piramidami.

Na początku trzeba wiedzieć, że starożytni Egipcjanie nie znali liczb niewymiernych. Na podstawie wniosków matematyka i historyka Eric'a Temple'a Bell oraz matematycznego papirusa Rihanda (źródle większej części współczesnej wiedzy o starożytnej matematyce egipskiej) utrzymujemy, że nie potrafili również obliczyć poszczególnych wielkości piramid, nie znając twierdzenia Pitagorasa. Jedynym trójkątem prostokątnym jaki znali był trójkąt $3 : 4 : 5$. Zauważono że spora część piramid egipskich ma proporcje zbliżone do tego szczególnego trójkąta.

Ostrosłup o takich proporcjach ma niemal identyczny kształt jak złoty ostrosłup. Kąt nachylenia ściany bocznej jest równy: $tg\alpha = \frac{4}{3} \Rightarrow \alpha \approx 53.13^\circ$. Jest to kąt bardzo zbliżony do tego ze złotego ostrosłupa tzn: $51.83^\circ$. Stąd spekulacje o obecności złotego podziału w piramidach egipskich, które są nieco przesadzone.

W połowie XI wieku Roger Herz-Fischler zajmował się badaniem Piramid egipskich. Zbadał między innymi Chefrena, Mykerinosa, niektóre z Gizy, Sakkary i Abusiru. W wyniku tych badań wysnuł sporo teorii matematycznych dotyczących kształtu piramid. Jedną z nich jest obecność trójkąta Keplera w piramidach egipskich, tak jak w złotym ostrosłupie. Zasugerowano również, że piramida Cheopsa ma najbardziej zbliżony kąt do złotego ostrosłupa. Wynosi on około $51.87^\circ$ Inne piramidy też są dość zbliżone: Chefrena, $52.33^\circ$ i Mykerinosa: $50.78^\circ$.

Piramida Cheopsa jest tym ciekawsza, że sporo historyków/ matematyków twierdzi, że wysokość ściany bocznej Wielkiej Piramidy w Gizie oraz połowa jej boku są w złotym stosunku. Twierdził tak na przykład piramidolog John Taylor w swojej książce „The Great Pyramid: Why Was It Built? and Who Built It?”. Wyjaśnienie tej zależności przypisuje się Ojcowi historii, greckiemu historykowi Herodotowi. Podobno stwierdził on, że wymiary Piramidy Cheopsa zostały tak dobrane, aby pole podstawy ostrosłupa o boku równym wysokości $H$ piramidy równało się polu ściany bocznej. Jeżeli jego założenia byłyby prawdziwe, to oznaczając połowę boku podstawy jako $a$ oraz wysokość ściany bocznej jako $h$ można wyliczyć: $$P_p = (2a)^2 = H^2$$ $$P_b = a\cdot h$$ $$a \cdot h = H^2 \quad \wedge \quad a^2 + H^2 = h^2$$ $$a \cdot h = h^2 – a^2 /:a^2$$ $$\frac{h}{a} \; – \; (\frac{h}{a})^2 + 1 = 0 \qquad t = \frac{h}{a}$$ $$x^2 – x – 1 = 0 $$ A takie równanie jest już nam bardzo dobrze znane. Jak wiadomo rozwiązaniem, tego równania jest liczba $\varphi$. Czy więc w piramidzie Cheopsa jest ukryty złoty podział? Tego nie wiemy i pewnie nigdy się nie dowiemy. W świecie są też inne teorie dotyczące wymiarów tej piramidy. Na przykład twierdzono, że stosunek obwodu podstawy do wysokości jest w dobrym przybliżeniu równy $2\pi$

Obecność złotego podziału w Partenonie, nie jest potwierdzone przez żadne prawdziwe pomiary. Na wielu stronach możemy znaleźć zdjęcia greckiego budynku, z wpisanym złotym prostokątem. Są to jednak zdjęcia pokroju wcześniej pokazanej „Mona Lisy” i „Ostatniej Wieczerzy”. Nie wiadomo czemu podstawa złotego prostokąta leży akurat na tym schodzie. Dlaczego została dobrana taka grubość konturów? Każdy może wybrać inny punkt odniesienia pomiarów aby dopasować wyniki do siebie.

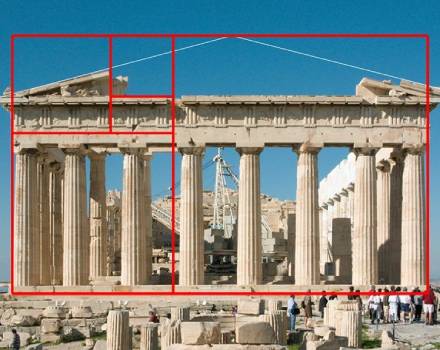
Po renowacji Partenonu jeszcze raz dokładnie zbadano jego wymiary. Żaden ich stosunek nie jest nawet zbliżony do złotej proporcji. Na przykład stosunek długości podstawy Partenonu wynosi: $\tfrac{69.5m}{30.9m} \approx 2.25$.
Jego wysokość to $13.72m$. Teraz: $\tfrac{69.5m}{13.72m} \approx 5.07$, $\tfrac{30.9m}{13.72m} \approx 2.25$.
Marvin Trachtenburg i Isabelle Hyman podali jeszcze inne wymiary: wysokość to 45 stóp, a szerokość 101 stóp. Ich stosunek to: 2,25. Jak widać nie można tu znaleźć boskiej proporcji. To, że Fidiasz użył liczby Phi do budowy Partenonu jest tylko mitem.

Jednym z nielicznych pewników wykorzystania złotego podziału w architekturze jest system modulor architekta Le Corbusiera. Zainspirowany proporcjami „Człowieka Witruwiańskiego” i pracą Adolfa Zeising'a stworzył własny system proporcji, który później niejednokrotnie wykorzystywał w swoich budowlach.

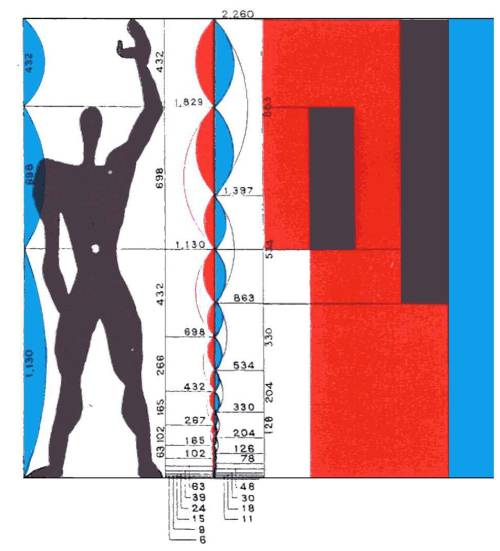
Jak widać na grafice system ten opiera się na człowieku o wzroście 1.83m, z podniesioną ręką. Ta przyjęta standardowa wielkość mężczyzny jest początkową wartością malejącego ciągu geometrycznego: $1,83m, 1.13m, 0.70m, 0.43m, 0.27m,...$
Kiedy podwoimy wysokość od stóp do pępka powstaje ciąg geometryczny oznaczony kolorem niebieskim: $2.26m, 1.40m, 0.86m, 0.54m,…$ Ilorazem obu ciągów jest złota liczba $\varphi$ Oprócz tego stosunek wzrostu człowieka do odległości od stóp do pępka także jest równy $\varphi$

Jedne z najbardziej znanych budynków w których jest zastosowany system modulor to: jednostka mieszkaniowa „Unité d’habitation” lub na przykład kościół „Sainte Marie de La Tourette” Budynki te są widoczne na zdjęciach. Oba te budynki znajdują się we Francji.

Z omówionej historii złotego podziału łatwo wywnioskować, że tak naprawdę boska proporcja przypadkowo znalazła się w świecie sztuki. Ale może jest jakiś sens używania go w celach estetycznych. Spróbujmy to sprawdzić na przykładzie złotego prostokąta. Który prostokąt z tych poniżej jest według ciebie czytelniku najpiękniejszy? Spróbuj go kliknąć.

Który prostokąt wybrałeś jako pierwszy? A może wybrałeś od razu złoty?

Podobne doświadczenie zostało przeprowadzone przez Gustava Fechnera. W jego eksperymencie brało udział 228 mężczyzn oraz 119 kobiet. Mieli za zadanie wybrać 1, 2, lub 3 prostokąty spośród dziesięciu, które najbardziej im się spodobały i te które najmniej (choć tu liczba badanych osób jest mniejsza). Jeżeli dana osoba wybrała jeden, to prostokąt ten otrzymał 1 punkt, gdy dwa to każdy z nich otrzymał po 0,5 i oczywiście w przypadku, gdy 3, to po 0,33 punktu. Wyniki eksperymentu znajdują się w poniższej tabeli. Duże $Z$ oznacza wyniki, gdy prostokąt został wybrany jako ten, który się podoba. Małe gdy przeciwnie. Ponadto, $m$ oznacza mężczyzn, a $w$ kobiety. W kolumnie $V$ wypisano wszystkie prostokąty. Funkcję złotego prostokąta pełnił ten o stosunku wymiarów 34:21 (oznaczony kółkiem z kropką).

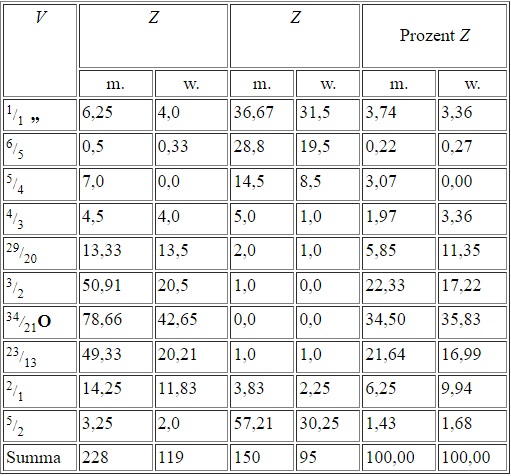
Okazało się że najlepsze wyniki zebrał złoty prostokąt. Może faktycznie złoty prostokąt jest tym najpiękniejszym, w którym ukryta jest harmonia.

Podobny eksperyment przeprowadził Joo Young i Petry Badke-Schaubopis.
Opisali go w swojej pracy:

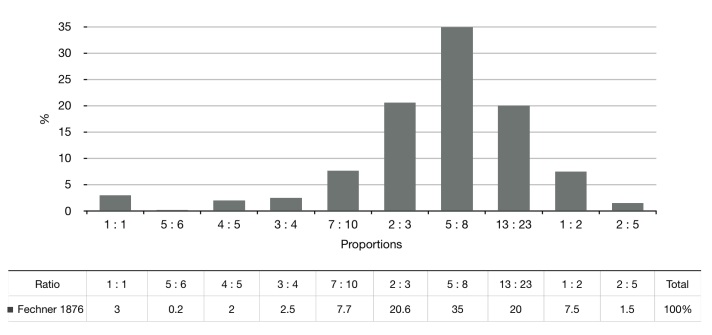
Jak widać zwyciężył prostokąt o proporcjach boków 7:10, zaś ten zbliżony do złotego (czyli 5:8) wypadł dosyć przeciętnie. Prostokąt ten nie jest jednak tak zbliżony do złotej proporcji jak ten z eksperymentu Gustava Fechnera. Pokazuje to, że nie każdy złoty prostokąt jest taki sam. Wybór najpiękniejszej figury zależy też od wielu czynników. Każdy ma swój ulubiony prostokąt. Tak naprawdę nie możemy stwierdzić, który jest najpiękniejszy. Możemy z tego wywnioskować jedynie, to że złoty prostokąt istotnie może mieć jakieś nieprzeciętne walory estetyczne.

Korzystając z instagrama, twitera, iphona czy z youtuba zastanawiałeś się kiedyś w jaki sposób powstały loga tych firm? Okazuje się, że jednym ze sposobów kreacji takiego loga jest użycie złotego podziału. Wykorzystuje się do tego siatkę złotych prostokątów, lub okręgów w nią wpisaną. W internecie dość często pokazuje się logo Instagrama i twittera z siatką złotych okręgów. Postanowiłem sam sprawdzić w programie graficznym jak to naprawdę wygląda.

Logo Twittera wykonałem od podstaw. Na gotowe logo instagram nałożyłem tylko siatkę złotych okręgów. W przypadku Twittera poszło mi dosyć łatwo i dostrzegłem zamysł stosowania tej metody. Natomiast jeśli chodzi o Instagram to nie widzę sensu używania tego. Trudno jest samemu zrobić takie jak to logo od podstaw przy użyciu złotego podziału. Tym sposobem sam możesz spróbować wykonać też własne ikony. Ogranicza cię tylko wyobraźnia.

Nie tylko ikony aplikacji można zaprojektować taką metodą. Kolejną rzeczą jest harmoniczny design strony, lub aplikacji mobilnych. Poniżej podałem jeden z pomysłów wykonania takiej strony. Tu posłużyła mi siatka złotych prostokątów.

Czy te firmy naprawdę użyły złotego podziału w swoich projektach? Moim zdaniem nie, (szczególnie w przypadku instagrama), jednak nie możemy tego wykluczyć. Z badań opisanych powyżej wynika, że złote prostokąty mają jakiś pierwiastek piękna w sobie. Na pewno ich zastosowanie nie było by bezsensowne, a wręcz przeciwnie, nawet pomocne. Na przykład sposób projektowania siatki strony aplikacji jest dośc łatwy.

Nieodłączną rzeczą social mediów są zdjęcia. Każdy kto trochę więcej zajmuje się robieniem fotografii na pewno słyszał o metodzie trójpodziału. Służy ona do odpowiedniego kadrowania. Polega ona na przecięciu pola obrazu dwoma liniami pionowymi i dwoma poziomymi. Dzielą one pole zdjęcia na 9 równych części. Miejsce przecięcia linii to tzw. mocny punkt obrazu, czyli miejsce gdzie w pierwszej kolejności wędruje nasz wzrok. Okazuje się, że w fotografii występuje tez inna bardzo podobna reguła – metoda złotego podziału. Tutaj dzielimy pole obrazu też na 9 części. Odcinki pionowe dzielą w złotym stosunku odcinki poziome i vice versa. Tu mocne punkty wyznacza się tak samo jak w metodzie trójpodziału.

Na obu fotografiach została użyta metoda złotego podziału. Na fotografii z krokodylem odcinki również wyznaczają przejścia między odrębnymi kolorami.