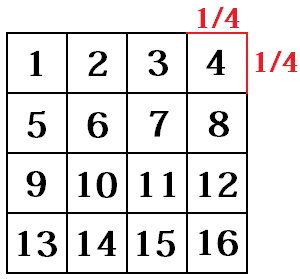
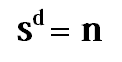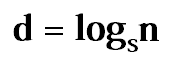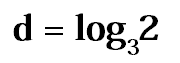Wymiar fraktalny (wymiar podobieństwa)

Samo słowo "fraktal" pochodzi od słowa frangere co w języku łacińskim oznacza "łamać". Nazwa ta jest trafna, ponieważ wymiar fraktala zazwyczaj nie jest liczbą całkowitą (wyjątkiem jest na przykład zbiór Mandelbrota). Trudno jest nam sobie jednak to wyobrazić, ponieważ jesteśmy przyzwyczajeni do dwu- lub trójwymiarowych figur i brył. 

Aby opisać położenie dowolnego punktu w świecie potrzebujemy trzech wymiarów - długości, wysokości i szerokości. Jednak aby opisać miejsce, w którym znajduje się przedmiot na stole wystarczą nam już tylko dwie współrzędne - długosć i szerokość, a do opisania pewnego miejsca na sznurze - tylko jedna współrzędna, która określa nam odległość od początku lub końca sznura. Takie podejście do pojęcia "wymiaru" pozwala nam lepiej spojrzeć na tzw. wymiar samopodobieństwa.

Matematycznie jednak, definiujemy wymiar w nieco inny sposób. Oparty jest on o koncepcję, w której daną figurę pokrywamy mniejszymi, podobnymi do wyjściowej. Przez to, że figury te nazywane są "pudełkami", wymiar przyjął nazwę wymiaru pudełkowego. Nazywamy nim potęgę, do której trzeba podnieść odwrotność skali, w jakiej podobne są mniejsze figury, aby otrzymać ilość nowo powstałych figur. Inną nazwą jest wymiar samopodobieństwa.

Na początek wyobraźmy sobie kwadrat, który pokrywamy mniejszymi kwadratami podobnymi do niego w skali 1/4 - otrzymamy 16 kwadratów. Żeby otrzymać 16, musimy 4 (odwrotność skali) podnieść do drugiej potęgi - kwadrat jest figurą dwuwymiarową! W ten sam sposób możemy spojrzeć na sześcian, dzieląc go na mniejsze sześciany w skali 1/3 lub odcinek podzielony na mniejsze w skali 1/2. Jeśli chcesz, policz to szybko w głowie!

Narzędziem, które służy do obliczenia, do jakiej potęgi należy podnieść liczbę s, aby otrzymać liczbę n jest logarytm.

Aby lepiej zrozumieć pojęcie wymiaru samopodobieństwa w odniesieniu do fraktali przeanalizujmy zbiór Cantora:

Każdy odcinek dzielimy na trzy, a następnie "wycinamy" środek. Każdy nowo powstały odcinek jest więc podobny do poprzedniego w skali 3, a z każdego odcinka powstają dwa nowe. Po podstawieniu do wzoru otrzymujemy wynik - wymiar fraktala wynoszący w tym wypadku 0,631.