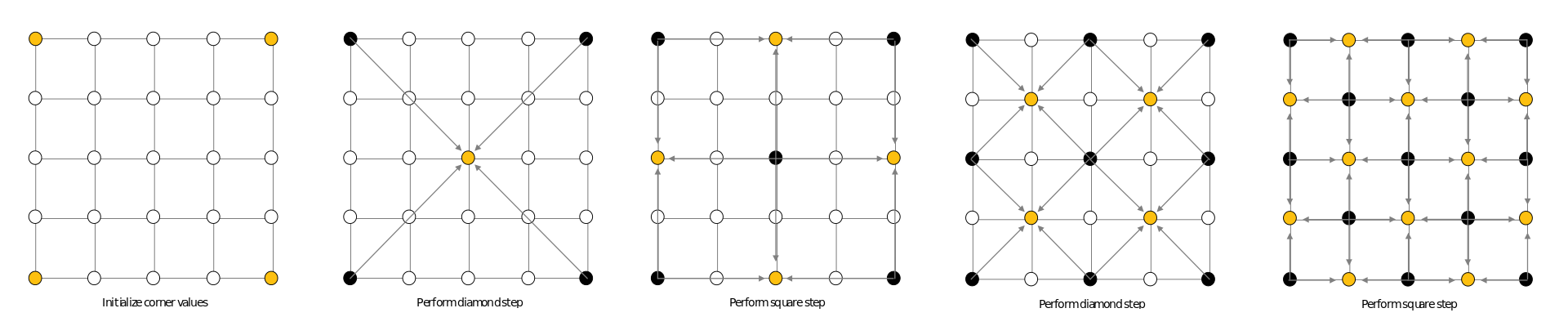
Mapy oraz obiekty
Jednym z praktycznych zastosowań fraktali jest generowanie różnego rodzaju map (znajdujących zastosowanie między innymi w grach) niosących za sobą różnorodne informacje. Mogą być to mapy wysokościowe, temperatur, rodzajów gleb i wiele innych.
Pozwalają one twórcom kreować dwu- lub trójwymiarowe tereny - a graczom cieszyć się różnorodnością rozgrywki. Fraktalnie generowane są też obiekty na mapach - zamiast ręcznie umieszczać każde źdźbło trawy, stosuje się programy komputerowe,
które automatycznie wykonują proste, powtarzalne czynności.

Przykładowa mapa