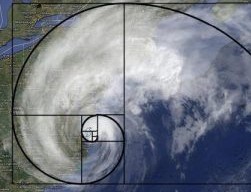
Ciąg Fibonacciego
„Φ jak Fibonacci”

[Źródło]
Zanim zapoznamy się z tym zagadnieniem, najpierw trochę historii, czyli kilka słów o samym twórcy, czy raczej odkrywcy niezwykłej zależności. Fibonacci, a właściwie Leonardo Pisano Fibonacci żył w latach ok. 1170 – 1250. Ów Włoch uznawany jest za jednego z najwybitniejszych średniowiecznych matematyków, co ciekawe sam jednak często używał pseudonimu „Bigollo”- znaczącego mniej więcej tyle co „nic nie wart” lub „podróżny”. To drugie- odnosi się do jego licznych wypraw, które odbywał już od wczesnego dzieciństwa. To właśnie wtedy nabywał wiedzę w dziedzinie matematyki i poznał m. in. arabski system liczbowy. Ogólnie ciekawiły go unikalne systemy liczbowe przyjęte w różnych regionach świata, tym jednak zainteresował się szczególnie. Starał się nawet wprowadzić ten system w ówczesnej Europie, w której do wykonywania obliczeń arytmetycznych używano cyfr rzymskich, metoda ta nie była jednak łatwa i miała kilka ograniczeń, wynikających m. in. z braku arabskiego odpowiednika zera.
„Króliki vs matematyka”
Wszystko zaczęło się od napisanej przez niego książki zatytułowanej „Liber Abaci”, w której Fibonacci postawił następujący problem:
„Pewien człowiek umieścił parę królików w miejscu otoczonym ze wszystkich stron murem. Ile par królików może być wyprodukowanych z tej pary w ciągu roku, jeśli zakłada się, że co miesiąc każda para rodzi nową parę, która od drugiego miesiąca staje się produktywna?”
Po rozpatrzeniu problemu i przedstawieniu go w formie tabelki, włoski matematyk otrzymał następujące wyniki:
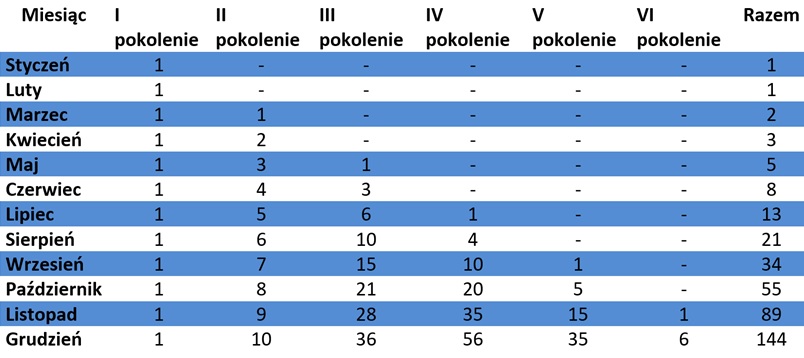
Okazało się, że łączna liczba królików w poszczególnych miesiącach tworzyła zadziwiający ciąg wyrazów. Kolejne liczby były bowiem sumą dwóch poprzednich. Liczby owe można więc tworzyć w nieskończoność, taki ciąg nazywany jest ciągiem rekurencyjnym, gdzie każdy kolejny wyraz jest zależny od poprzednich.
„Złota liczba”
Dobrze, zatem czym jest w ogóle cała ta złota liczba i jaki ma związek z naszym ciągiem? Zacznijmy więc od pierwszego zagadnienia. Złotą liczbę graficznie przedstawiamy przy pomocy symbolu Φ (czyt. „fi”). Jest ona ściśle związana z tak zwanym złotym podziałem. Podział ów polega na takim podzieleniu odcinka na dwie części, aby stosunek długości dłuższego odcinka do długości krótszego odcinka, był taki sam, jak stosunek długości dłuższego odcinka do długości całego odcinka. Spójrzmy na poniższy rysunek przedstawiający to zagadnienie w sposób graficzny.
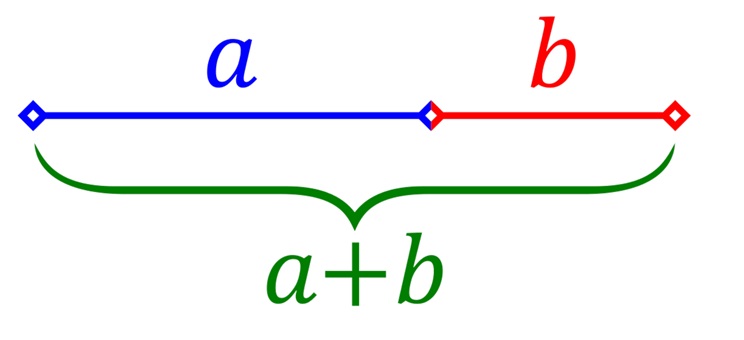
[Źródło]
Zgodnie z powyższym prawdziwe jest więc stwierdzenie, że:
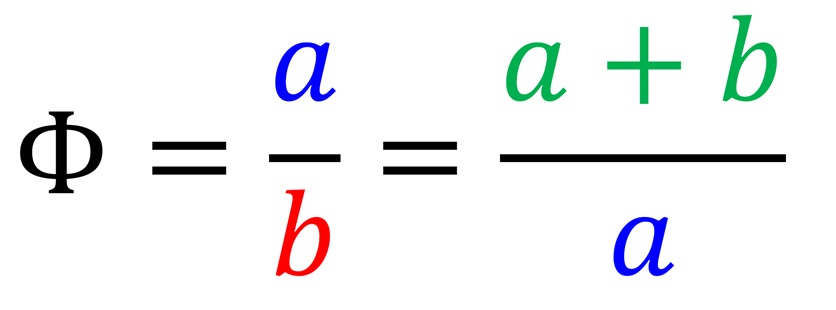
Spróbujmy więc teraz rozwiązać powstałe równanie i wyznaczyć wartość Φ.
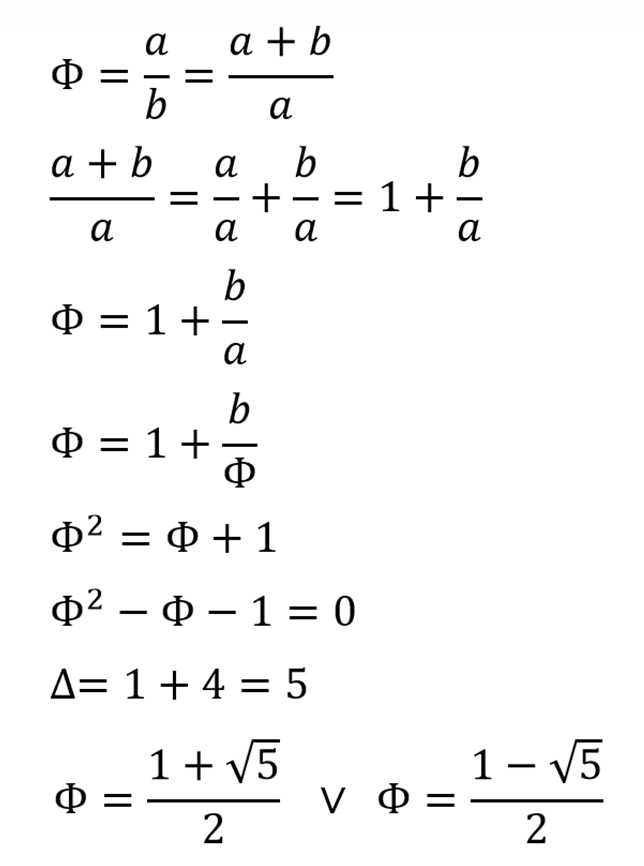
Przy pomocy kalkulatora możemy obliczyć, że pierwsze rozwiązanie, a zatem złota liczba, wynosi w przybliżeniu 1.61803399.
Drugie rozwiązanie w tym przypadku powinniśmy odrzucić, ponieważ wyznaczaliśmy długość odcinka, nie może więc być ona wartością ujemną. Warto jednak zastanowić się nad jej wynikiem, ponieważ przyda nam się on troszkę później. W przybliżeniu jest to -0,61803399, czyli tyle ile wynosi liczba przeciwna do odwrotności liczby Φ.
Dobrze to teraz skoro wiemy już mniej więcej czym właściwie jest nasza wyjątkowa liczba, możemy przejść do drugiego zagadnienia. Przypomnijmy zatem jak wygląda ciąg Fibonacciego i obejrzyjmy krótki filmik.
Teraz widzimy już wyraźnie niezwykły wręcz związek między ciągiem Fibonacciego, a liczbą Φ. Możemy też stwierdzić, że granicą ciągu Fibonacciego jest właśnie „złota liczba”.
„Wzór Ciągu Fibonacciego”
Ciąg określony jest rekurencyjnie. Są dwa poglądy na to czy ciąg powinien zaczynać się od 0 czy od 1. Biorąc jednak pod uwagę fakt, że ciągi opieramy o liczby naturalne takie, że n>0, częściej spotkać możemy ciąg zaczynający się od liczby 1. Choć wzór rekurencyjny może również zaczynać się od 0.

„Złota spirala”
Będąc przy temacie ciągu Fibonacciego nie można oczywiście pominąć tego zagadnienia. Jest ono bardzo pasjonujące i ciekawe, zwłaszcza jeśli zacznie się ją dostrzegać w codzienności, ale o tym za chwilę. Wróćmy zatem do sedna. Złotą spiralę można nazwać graficzną interpretacją ciągu Fibonacciego. Przedstawia się ona w następujący sposób.
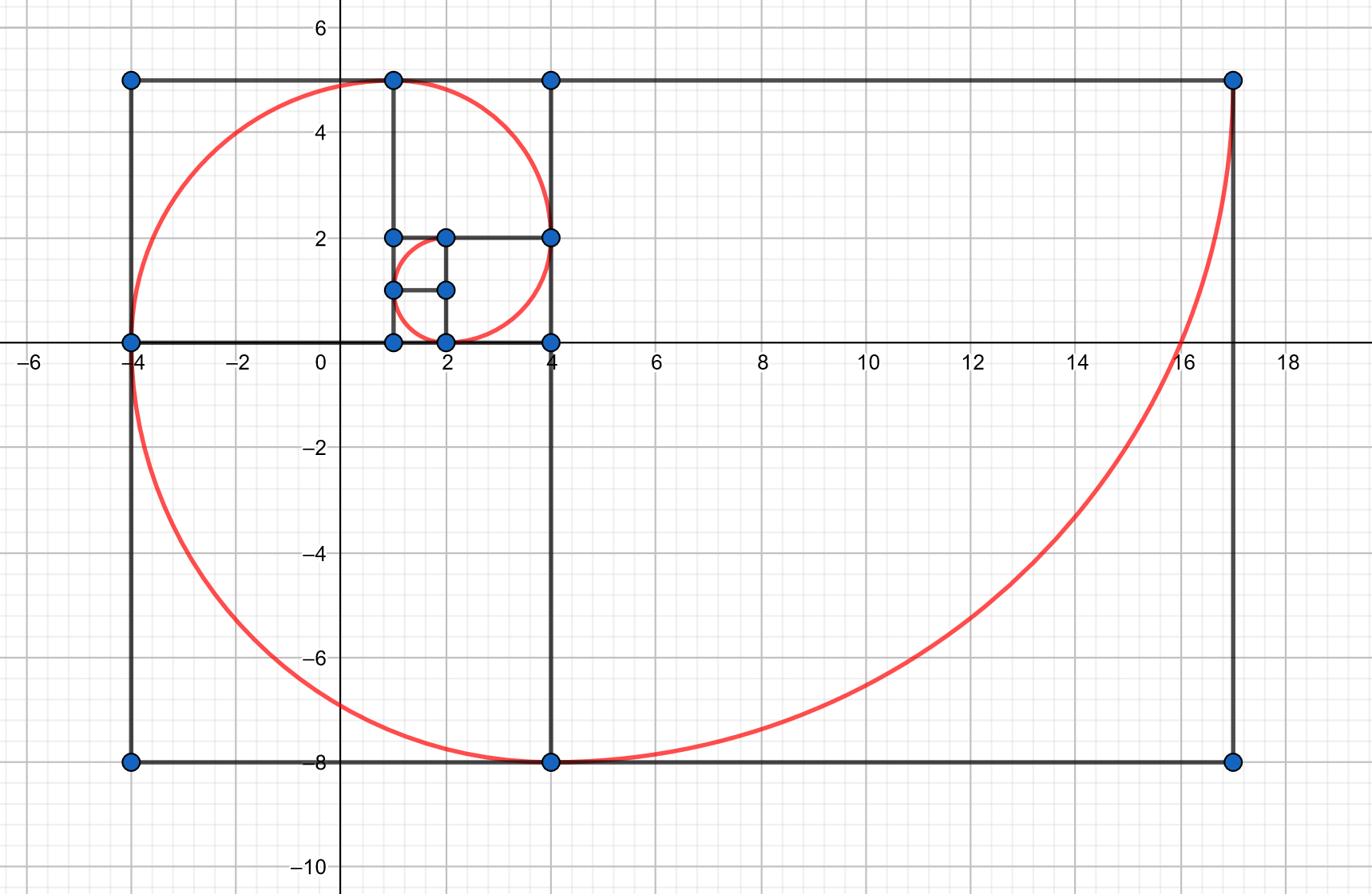
Powyżej przedstawiono tylko fragment spirali, ponieważ każde kolejne elementy można byłoby, rzecz jasna, dodawać w nieskończoność. Warto tutaj zauważyć, że stosunek długości odpowiednich boków kwadratów jest równy Φ.
Podsumowując- kształt geometryczny tzw. złotej spirali opisują liczby Fibonacciego oraz złota proporcja.
„Fibonacci na co dzień”
Każdy z nas miał kiedyś w ręku kwiatek, lub przynajmniej go widział, ale niewiele z nas kiedykolwiek zdawało sobie sprawę z tego, że ilość płatków to właśnie liczby Fibonacciego. Przyjrzyjmy się temu bliżej.
Znamy już skądś podobną sekwencję prawda? Ale to nie wszystko okazuje się bowiem, że nawet ilość kolejnych pędów czy gałęzi drzew również tworzy ciąg Fibonacciego i jest on wtedy określany mianem spiralnej filotaksji.
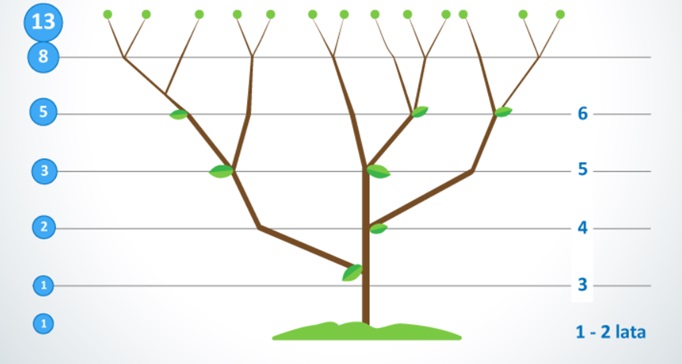
[Źródło]
Ale właściwie skąd się to wszystko bierze? Czyżby rośliny kochały Fibonacciego? Tej drugiej kwestii może nie będę rozstrzygać, ale odpowiedź na pierwsze pytanie, okazuje się być całkiem prosta. Rośliny przestrzegają tak ściśle liczb Fibonacciego, ponieważ taki rozwój jest dla nich po prostu korzystny. To ułożenie pozwala w pełni wykorzystać dostępne światło, potrzebne im do przeprowadzenia fotosyntezy. Żaden liść nie może więc nachodzić na poprzedni i tutaj pojawia się kolejne „złote” pojęcie- mianowicie złoty kąt, którego wartość wynosi ok. 137,5° (jest on oczywiście również oparty na liczbach Fibonacciego). Każdy wyrastający z merystemu liść układa się właśnie pod złotym kątem w stosunku do poprzedniego.
Myślę, że teraz czas na pokazanie obecności złotej spirali w otaczającej nas rzeczywistości. Zacznijmy może od huraganów. Dla przykładu poniżej huragan Sandy i Irene wpisane w złotą spiralę.
To może teraz dla odmiany coś nie z tej Ziemi?
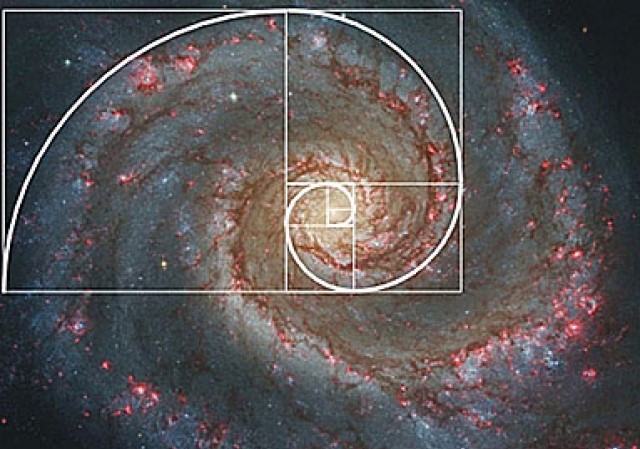
[Źródło]
I moje ulubione muszelki prosto znad morza :).

[Źródło]
Myślę, że warto również wspomnieć, że złotą proporcję możemy odnaleźć także w budowie naszego ciała. Oczywiście nie u każdego będzie ona idealna, ale na pewno będzie przynajmniej zbliżona. Za przykład mogą posłużyć nam chociażby nasze dłonie.

[Źródło]
Mamy zatem 2 dłonie, każda z nich składa się z 5 palców. Przy czym w sumie 8 palców składa się z 3 paliczków, natomiast dwa kciuki składają się z 2 paliczków. Również stosunki długości palców odpowiadają liczbą Fibonacciego. Dodatkowo stosunek środkowego palca do małego wynosi Φ.
Obecności złotej liczby i złotej proporcji oczywiście nie mogło zabraknąć także w architekturze i malarstwie. Już starożytni Grecy znali te niezwykłe i harmoniczne proporcje, tworząc m. in. Partenon.

[Źródło]
Na koniec rzućmy jeszcze okiem na malarstwo, a za przykład niech posłuży jedno z najsłynniejszych dzieł Leonarda da Vinci – „Mona Lisa”.

[Źródło]
Dzięki zachowaniu złotej liczby, złotej proporcji i zastosowaniu liczb Fibonacciego, twórcy nadawali, zarówno dziełom sztuki jak i architektury- wyjątkowego spokoju i harmonijnego porządku.