Ciąg Lucasa
„Słów kilka…”

[Źródło]
Skoro ciąg Fibonacciego mamy już za sobą, warto też przyjrzeć się innym ciągom. Najpierw jednak trochę o samym twórcy. François Édouard Anatole Lucas był francuskim matematykiem, urodził się w 1842 roku, zmarł zaś w 1891. Zafascynował się ciągiem Fibonacciego i poświęcił wiele czasu na jego badanie. Jednym ze skutków jego pracy było stworzenie wzoru pozwalającego określić n-ty wyrazu tegoż ciągu. Interesował go też rozrywkowy wymiar matematyki, co przyczyniło się do stworzenia przez niego gry zwanej Wieże Hanoi. Pośród jego dokonań wymienia się również opracowanie testu pozwalającego na badanie pierwszości liczb, które później dopracował inny matematyk Lehmer. W taki właśnie sposób powstał tzw. test Lucasa-Lehmera, biorący swoją nazwę od nazwisk jego twórców. Dobrze skoro wiemy już trochę o naszym matematyku, przejdźmy do konkretów.
„To ciąg Fibonacciego nie jest wyjątkowy?”
Zacznijmy może od filmiku.
Jak widzieliśmy- właściwie liczby, które wybierzemy jako pierwsze nie mają znaczenia, jeśli stosujemy zasadę, że każdy wyraz powstaje rekurencyjnie jako suma dwóch poprzednich. Jest to tzw. złota zasada, która zawiera się we wzorze:
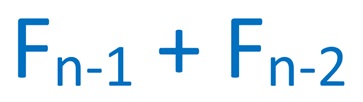
To właśnie dzięki badaniom Lucasa okazuje się, że tak naprawdę ciąg Fibonacciego nie jest jedyny w swoim rodzaju, a raczej stanowi zaledwie jedną z ogromnej grupy ciągów o podobnych własnościach. Fibonacci był jednak pierwszym, który jedną z takich sekwencji przedstawił.
„Udowodnij albo nie istnieje”
No cóż oczywiście, że udowodnienie tego w sposób matematyczny jest jak najbardziej możliwe. Żeby było trochę łatwiej, w tym celu posłużę się znanym nam już ciągiem Fibonacciego, zatem spójrzmy.
Chyba skądś już kojarzymy te wyniki, prawda? Takie same otrzymaliśmy kiedy wyznaczaliśmy Φ ze złotego podziału odcinka. Wyniki które otrzymaliśmy to rzecz jasna: wartość złotej liczby a także tzw. „małe phi”, a dokładnie „minus małe phi”- wynik ten otrzymamy kiedy podzielimy dany wyraz nie przez poprzedni, czyli mniejszy od niego, ale przez następny- większy; minus wskazuje właśnie na odwrócenie kolejności dzielenia danych wyrazów.
„Lucasa pod lupę”
Przyjrzyjmy się jak właściwie wygląda ciąg tego francuskiego matematyka. Jest on tworzony na takiej zasadzie:

Zatem jego początkowe wartości prezentują się w ten sposób:
2 1 3 4 7 11 18 29 47 76 123 199 322 521 843 1364 ...
No cóż, właściwie nic ciekawego prawda? Teraz w waszych głowach rodzą się zapewne pytania „I co? I to jest ten niezwykły i sławny ciąg? W czym on jest niby lepszy od ciągu Fibonacciego, czy wspaniałego ciągu Aleksandry?". No dobra z tym ostatnim to może przesadziłam :). Wracając jednak do temtu, na pierwszy rzut oka, rzeczywiście nie ma tutaj absolutnie nic szczególnego. Ot liczby jak liczby, jak każde inne. Spójrzmy jednak na obrazek poniżej, który przedstawia kolejne potęgi liczby Φ.

Tak, wiem może nie jest to widoczne na pierwszy rzut oka, ale zaokrąglijmy teraz te liczby.

Teraz właśnie możemy zobaczyć tą niezwykłą właściwość. Wyraźnie widzimy, że zaokrąglenia następnych potęg liczby Φ odpowiadają kolejnym liczbom Lucasa. Ta prawidłowość występuje w tym przypadku zawsze, niezależnie od tego czy weźmiemy 5 wyraz ciągu, czy nawet 174. W efekcie oznacza to więc, że ciąg Lucasa jest nawet ściślej związany ze złotą liczbą, niż ciąg Fibonacciego!
„Lucas, a Fibonacci”
Bardzo ciekawa jest też zależność pomiędzy obydwoma tymi ciągami. Spójrzmy poniżej.

Jak widzidzimy suma wybranych dwóch wyrazów z ciągu Fibonacciego, odpowiada kolejnym wyrazom ciągu Lucasa.
Wróćmy jeszcze na moment do ciągu Fibonacciego. Po wypisaniu kolejnych jego wyrazów, kiedy przyjrzymy się ostatnim cyfrom, będziemy mogli zauważyć powtarzający się w nieskończoność okres 60 cyfr. Nie wiem jak Wam, ale mnie liczba 60 kojarzy się z zegarem, narysujmy więc okrąg i wpiszmy w niego powtarzające się cyfry.

Na naszym "zegarze", popatrzmy na godzinę 12, 3, 6 i 9 (zaznaczone czeronymi liniami). Okazuje się że w tych miejscach występuje liczba zero! Sprawdźmy, co z pozostałymi "godzinami" (zielone linie). Tutaj z kolei mamy same cyfry 5. Jest jeszcze jedna ciekawa zależność. Wróćmy do godzin 12, 3, 6 i 9. Wokół nich w takim samym ułożeniu znajdują się kolejno cyfry: 1, 7, 9 oraz 3! Dobrze, ale co w tym takiego niezwykłego? Otóż okazuje się, że ma to związek z liczbami pierwszymi (o których więcej będzie za chwilę). Spójrzmy na sto początkowych liczb pierwszych.
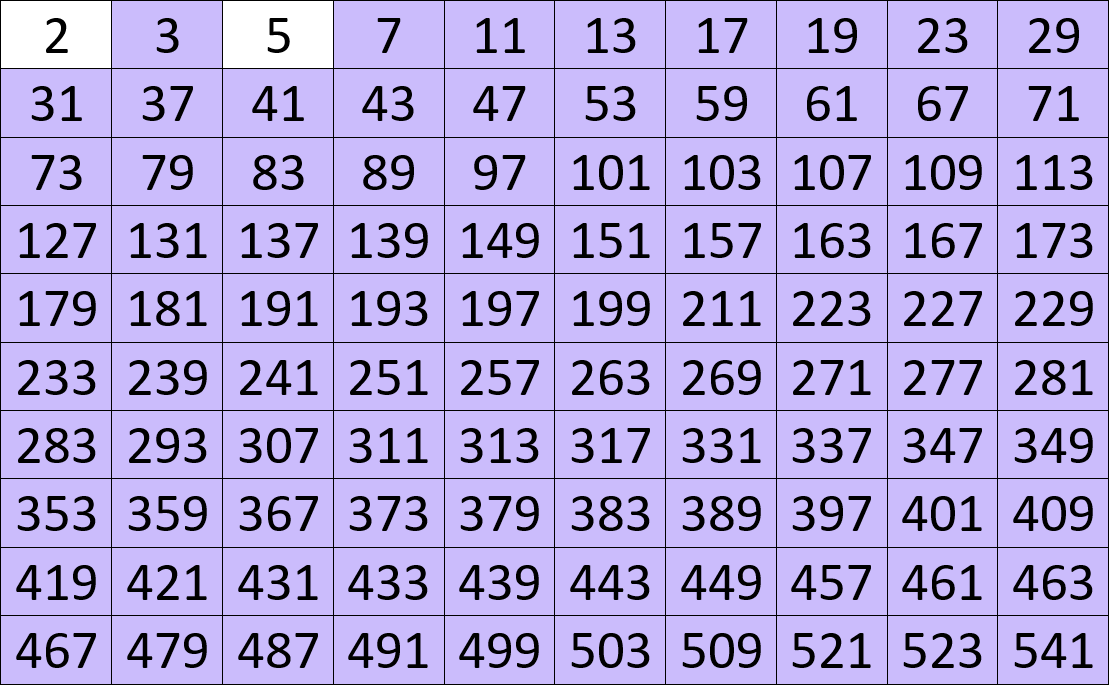
Kolorem zostały zaznaczone te liczby, które kończą się na jedną z tych czterech cyfr. Oprócz 2 i 5 są to tak naprawdę wszystkie pozostałe liczby pierwsze. Niezwykłe, że to właśnie te cyfry ułożyły się nam przy głównych godzinach naszego "zegara", prawda?
„A co z Lucasem?”
Widząc powyższą zależność, ktoś może powiedzieć: "No dobra, fajnie, ale to był ciąg Fibonacciego, a co z ciągiem Lucasa? W końcu on też należy do tej samej rodziny złotych ciągów." Racja weźmy więc teraz na tapetę ciąg Lucasa.
W tym przypadku nie trzeba wypisywać zbyt wielu liczb, aby sprawdzić czy tutaj będzimy mieli podobną cykliczność. W ciągu, którym się teraz zajmujemy taki okres powtarzania się ostatnich cyfr wynosi 12 liczb. Są to:
2 1 3 4 7 1 8 9 7 6 3 9
Wróćmy teraz do naszego "zegara" i sprawdźmy czy możemy gdzieś dostrzec powyższe cyfry.

Może nie są one widoczne na pierwszy rzut oka, ale wystarczy tylko zsumować wartości sąsiednie naszych pełnych "zegarowych" godzin. W tych miejscach, w których wychodzą nam liczby dwucyfrowe, bierzemy pod uwagę tą ostatnią i w taki oto sposób możemy podziwiać kolejną zależność między oboma ciągami.
Spróbójmy teraz zsumować wartości całego koła, a tekże prawej i lewej połówki
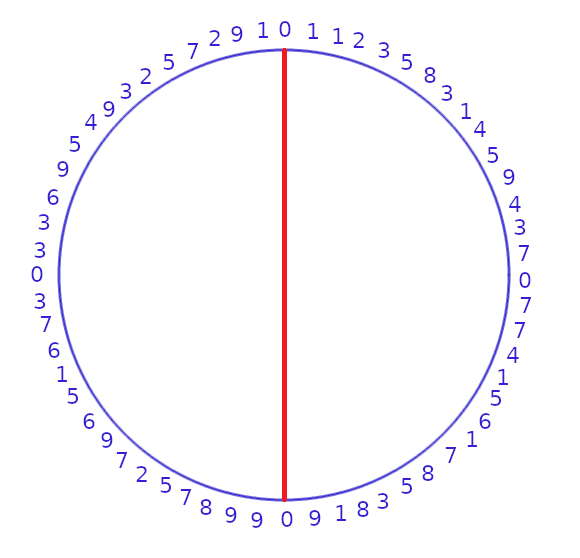
No cóż właściwie to nie otrzymaliśmy jakichś szczególnych wyników. Wartość dla całego koła wynosi 280, dla lewej połówki wynosi 152, a prawej 128. Spróbujmy więc zrobić z tym kołem coś innego.
Euklides w swojej pracy "Elementy" poruszył wiele kwestii związanych z geometrią (m. in. wspomniany przeze mnie wcześniej złoty podział). Nas jednak teraz najbardziej interesuje ten fragment, w którym matematyk daje odpowiedź na pytanie: "Jak geometrycznie wyznaczyć środek odcinka?". Mając do dyspozycji cyrkiel, możemy wbić jego nóżkę w punkt A i odmierzyć długość odcinka |AB|, następnie rysujemy okrąg i analogicznie postępujemy z punktem B. Miejsca przecięcia się okręgów wyznaczają nam środek odcinka |AB|. W efekcie otrzymujemy ciekawą figurę, która nosi dumną nazwę "rybi pęczerz".

Super, cytując klasyka można powiedzieć "mamy to", ale właściwie po co ja o tym mówię? Zaraz zobaczycie. Wróćmy do naszych poprzednich rozważań związanych z "zegarem", ale zastosujmy dodatkowo, przedstawioną wyżej metodę połowienia odcinka Euklidesa.
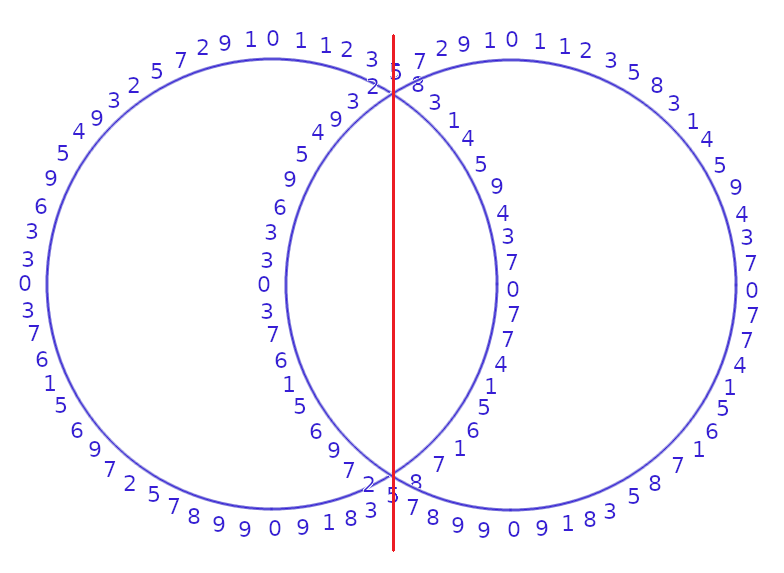
Zsumujmy teraz zewnętrzne wartości kół, w efekcie otrzymujemy wynik 360, no i to zdecydowanie bardziej pasuje nam do koła. To teraz dodajmy wartości wewnętrzne tych okręgów. Tutaj wynik też jest całkiem obiecujący- 180. Następnie sprawdźmy co w przypadku lewgo zewnętrznego łuku- tutaj otrzymujemy kolejny sympatyczny wynik- 180, podobnie jest z prawym zewnętrznym łukiem. Zostały nam więc już tylko łuki wewnętrzne lewy- 90, podobnie prawy.
Z pozoru nie mające nic wspólnego z okręgiem ostatnie cyfry liczb Fibonacciego, zapisane w formie okręgu, dopiero w parze dały takie piękne kojarzące się jednoznacznie wartości. Matematyczne powiązania są naprawdę niezwykłe...