Chyba każdy z nas zna definicję liczb pierwszych, jednak powtórek nigdy za mało, dlatego przypomnijmy ją sobie. Liczby pierwsze- to takie liczby naturalne większe od 1, które posiadają dokładnie dwa dzielniki: 1 i samą siebie. Poniższa tabelka przedstawia liczby pierwsze w przedziale od 1 do 100.

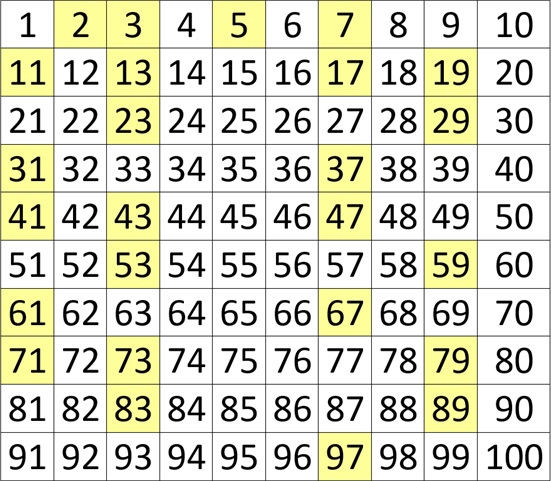
Nie wiem jak Was, ale mnie zawsze ciekaiwło dlaczego włściwie 1 nie jest liczbą pierwszą. Przecież teoretycznie spełnia warunek, bo dzieli się przez 1 i przez samą sibie. Przyjrzyjmy się bliżej tej sprawie.

„Wiecznie samotna... :(”

Mamy w matematyce wiele różnych twierdzeń, nam jednak, aby dowiedzieć się dlaczego cyfra 1 nie należy do liczb pierwszych, na razie wystarczy jedno. Nazywa się ono "Podstawowym twierdzeniem arytmetyki". Brzmi ono tak:

Każdą liczbę naturalną większą od 1, nie będącą liczbą pierwszą, można jednoznacznie przedstawić w postaci iloczynu liczb pierwszych.

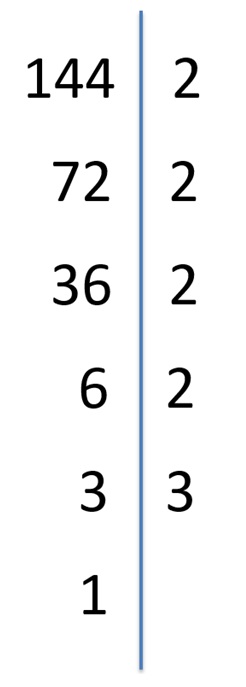
Widzimy teraz, że liczba 144 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3. W ten sposób zastosowaliśmy właśnie "Podstawowe twierdzenie arytmetyki"- jednoznacznie przedstawiliśmy 144 w postaci iloczynu liczb pierwszych. Zastanówmy się jednak, co stałoby się w przypadku, gdyby 1 była liczbą pierwszą. Wówczas liczbę 144 moglibyśmy przedstawić w taki sposób:

144 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 1

Albo tak:

144 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 1 ∙ 1

Albo tak:

144 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 1 ∙ 1 ∙ 1

Albo ta... No dobra może już wystarczy. W każdym razie moglibyśmy robić tak w kółko. Wróćmy zatem do naszego twierdzenia:

Każdą liczbę naturalną większą od 1, nie będącą liczbą pierwszą, można jednoznacznie przedstawić w postaci iloczynu liczb pierwszych.

"... można jednoznacznie przedstawić...", ja tymczasem uznając 1 za liczbę pierwszą przedstawiłam liczbę 144 na 3 różne sposoby. Zatem nie spełnia ona warunku tego twierdzenia i dlatego właśnie nasza biedna, samotna 1 nie może być uznana za liczbę pierwszą.

„Odkrycie Eulera”

Zostawmy już naszą samotniczkę w spokoju i przejdźmy dalej. Z wspomnianego wyżej twierdzenia, wiemy także, że liczby pierwsze są w pewnym sensie atomami świata matematyki (z gr. atomos- znaczy dokładnie tyle co "niepodzielny"), z których przy pomocy mnożenia możemy zbudować pozostałe liczby. Co ciekawe liczby pierwsze zdają się na pierwszy rzut oka występować całkowicie losowo, bez jakiegokolwiek określonego wzoru czy zasady. Są miejsca, w których liczby te wyrastają, niczym grzyby po deszczu, w innych z kolei występują absolutne pustynie, gdzie odstęp między kolejnymi liczbami pierwszymi wynosi nawet 72 liczby!

Jednym z pierwszych matematyków, który próbował rozwikłać zagadkę liczb pierwszych był Szwajcar- Leonhard Euler (1707-1783). Był prawdziwym geniuszem matematycznym i dokonał wielu odkryć zarówno w dziedzinie matematyki, jak i fizyki. Co dokładnie łączy go z tajemnicą liczb pierwszych?

Przede wszystkim Euler uważał, że liczby pierwsze to nie tylko losowe i abstrakcyjne wartości. Według niego liczby pierwsze mają bezpośredni związek z otaczającą nas rzeczywistością i są niejako kluczem do poznania praw przyrody. Do zwizualizowania rozpatrywanego problemu użył trochę niecodziennej metody. Zastosował bowiem schody, gdzie każda nowa liczba pierwsza to kolejny stopień. Metodę tę nazwał "Schodami liczb pierwszych".

[Źródło]

Choć nie poddawał się, nie potrafił jednak znaleźć żadnej prawidłowości, która rządiłaby tymi liczbami.

Tymczasem współcześni uczeni odnosili się do jego badań z rezerwą, niektórzy nawet wprost krytykowali jego starania. Euler jednak odkrył coś, co całkowicie uciszyło kpiące z niego osoby. Spójrzmy poniżej.

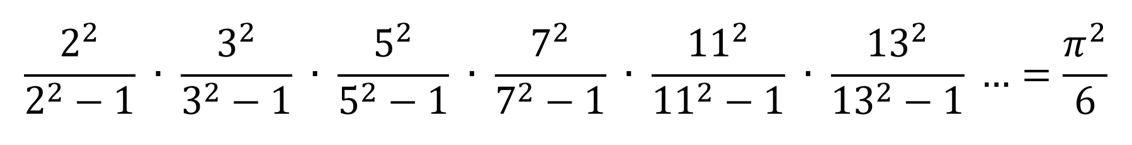
Równanie to w pełni składa się z liczb pierwszych, Euler ułożył je rozwiązując inny problem matematyczny. Nikt nie spodziewał się wówczas otrzymania jakiegokolwiek sensownego wyniku, jednak to, co Euler otrzymał było zaskakujące. Otóż okazało się, że liczby, którymi jak wówczas uważano rządzi chaos, mają związek ze stałą opisującą koło, czyli najpiękniejszy kształt we wszechświecie! Euler jako pierwszy wykazał, że liczby pierwsze mogą rzeczywiście mieć związek z prawami fizyki, a ich ułożenie nie jest do końca przypadkowe.

„Spirale Ulama”

Stanisław Ulam (1909-1984) również udowodnił, że występowanie liczb pierwszych nie może być przepadkowe (to tak jakbyście jescze nie uwierzyli ;) ). Jak tego dokonał? No cóż, właściwie to przyczynił się do tego nudny wykład, w którym nasz rodak uczestniczył. Z nudów stworzył sobie wówczas na papierze kwadratową spiralę liczb, wyglądała ona mniej więcej w taki sposób:

Ulam dostrzegł w tej spirali coś więcej i zaznaczył kreskami (jak na animacji) miejsca w których znajdują się liczby pierwsze. Okazało się, że występują one na liniach diagonalnych, czyli skośnych. Poniżej trochę większa spirala Ulama.

[Źródło]

Czarnymi kropkami oznaczone zostały liczby pierwsze. Natomiast na czerwono zaznaczyłam te, które występują skośnie. Jednak żeby mieć porównanie i pewność, że to nie nasz umysł jest już przemęczony i sam z siebie doszukuje się czegoś, co nie istnieje, przyjrzyjmy się jeszcze spirali losowych liczb (po lewej) i porównajmy ją ze Spiralą Ulama (po prawej).

[Źródło]

[Źródło]

Teraz wyraźnie widzimy, że spiralą Ulama rządzi jakiś niezwykły porządek. Możemy także stworzyć spiralę okrągłą- jest to tzw. Spirala Sacks'a, która jeszcze wyraźniej pokazuje wyjątkowe ułożenie tych liczb.

Wzdłuż czerwonej prostej zaznaczone są kwadraty liczb, a teraz żeby sobie to lepiej zobrazować, poniżej podobna spirala z większą ilością liczb. Czarne kropki to liczby pierwsze. Natomiast ta pusta przerwa bierze się z faktu, że żadna liczba podniesiona do kwadratu nie będzie liczbą pierwszą.

[Źródło]

Nie wiem jak Wy, ale ja wyciągnęłam z tego dwa wnioski: po pierwsze czasami warto nie uważać na lekcji, bo można dokonać niesamowitego matematycznego odkrycia, a po drugie bazgroły mają na to ewidentnie pozytywny wpływ ;).

„Liczby pierwsze Mersenne'a”

Zanim przejdziemy do sedna sprawy, warto też zapoznać się z innym matematykiem, który również dołożył swoją cegiełkę w całym procesie poznawania liczb pierwszych. Tym razem będziemy mówić o Marinie Mersenneie- francuskim matematyku, filozofie i teologu. Stworzył on ciąg liczb, które później od jego nazwiska nazwano Liczbami Mersenne'a. Każda liczba tego ciągu powstaje jako kolejna potęga liczby 2, pomniejszona o 1.

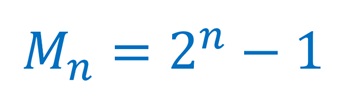
Ciąg Mersenne'a bedzie zatem wyglądał następująco:

1  3  7  15  31  63  127  255  511  1023  ...

Od razu możemy zauważyć, że nie wszystkie liczby Mersenne'a należą do liczb pierwszych, np. 1, 15, czy 63. Jaki sens ma zatem ten ciąg? Właściwie wbrew pozorom jest on całkiem użyteczny, szczególnie biorąc pod uwagę, że chociażby systemy logiczne naszych komputerów oparte są na systemie binarnym, czyli dwójkowym. Możemy więc stworzyć algorytmy wyszukujące następne liczby pierwsze.

Poza tym liczby pierwsze z tego ciągu mają inną ciekawą właściwość. Są one w bezpośredni sposób powiązane z tzw. liczbami doskonałymi- jest to taka liczba naturalna, która jest jednocześnie sumą swoich dzielników. Liczbą doskonałą będzie więc, np. 6

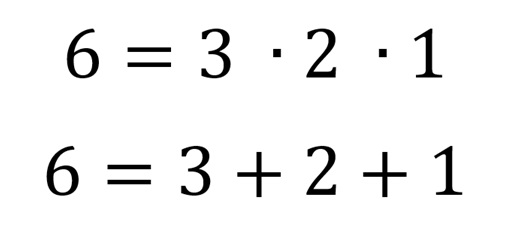
Innymi liczbami doskonałymi są np. 28, 496, czy 8128. Spróbujmy to teraz odnieść do liczb pierwszych Mersenne'a. M niech oznacza liczbę pierwszą Mersenne'a. Skorzystamy z takiego wzoru:

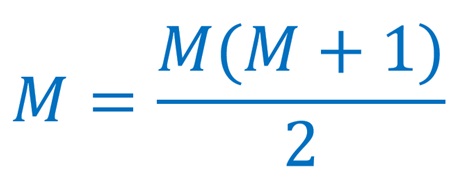
Teraz weźmy jedną z liczb pierwszych Mersenne'a i podstawmy do wzoru, niech to będzie np. 3.

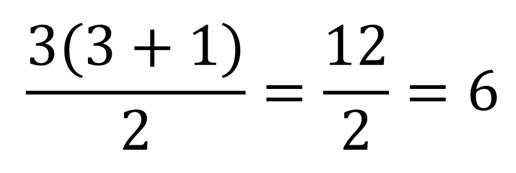
Żeby być pewnym na 100% weźmy jescze jedną liczbę i podstawmy do wzoru. Kolejną liczbą pierwszą w ciągu Mersenne'a jest 7.

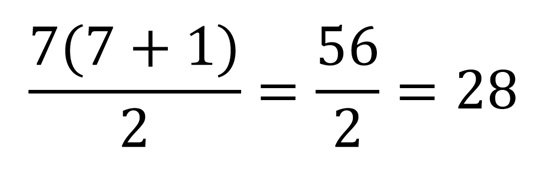
Tak jak wspominałam wcześniej, 28 jest również liczbą doskonałą, czyli to rzeczywiście działa. Zaskakujące jak matematyka potrafi być niezwykła i ile różnych, ciekawych zależności można się w niej doszukać.

„Zagadka wszechczasów”

Wreszcie dotarliśmy chyba do najważniejszej części artykułu. Owa tajemnicza "zagadka wszechczasów" to tzw. Hipoteza Riemanna. Bernhard Riemann (1826-1866) to niemiecki matematyk, który zainspirował się dowodem przeprowadzonym przez Eulera. Riemann uogólnił rozważania i lekko zmodyfikował pracę swojego poprzednika. W miejsce "2" wpisał "x", a całą sekwencję określił mianem funkcji ζ (czytaj: "dzeta"). Jego równanie miało więc postać:

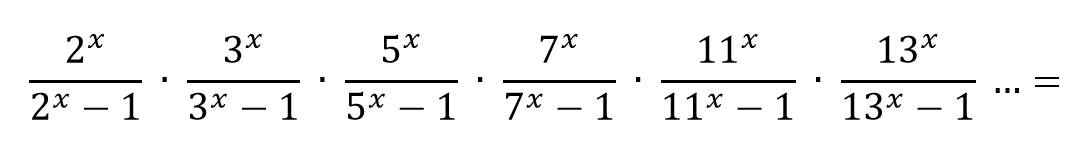
Dla łatwiejszego zrozumienia Riemann przedstawił swoją funkcję w wersji 3d. Następnie zabrał się za wyznaczanie jej miejsc zerowych. Początkowo przewidywano, że skoro funkcję ζ określają, jak wówczas uważano, "przypadkowo układające się" liczby pierwsze (my już wiemy, że to nie prawda), to również miejsca zerowe będą ułożone chaotycznie. W zasadzie mój komentarz jest już niepotrzebny, bo na pewno domyślacie się, że tak nie było. Jak więc się ułożyły?

Po obliczeniu czterech pierwszych miejsc zerowych, Riemann odkrył ciekawą prawidłowość. Okazało się bowiem, że każde z nich leżało dokładnie na linii prostej.

[Źródło]

Następnie Rimann sformułował swoje odkrycie w następujący sposób:

Wszystkie nietrywialne miejsca zerowe funkcji ζ leżą na linii prostej

Brzmi trochę dziwnie i obco, ale sprowadza się dokładnie do tego, co widzimy na obrazku powyżej. Hipoteza Riemanna przyniosła swoisty przełom w kwestii liczb pierwszych, ponieważ zamieniła abstarkcyjne pytanie: "Czy liczby pierwsze układają się nieprzypadkowo?", na konkretny problem matematyczny: "Czy wszystkie miejsca zerowe leżą na prostej?"

Od tego czasu, najwybitniejsci matematycy, chcący złamać kod liczb pierwszych, zawzięcie próbowali udowodnić tą hipotezę. Wielu z nich rujnowało sobie nawet życie.

„Brytyjski duet”

[Źródło]

[Źródło]

Na początku XX w. próbę rozwiązania tej hipotezy podjęła dwójka wspaniałych brytyjskich matematyków- John Littlewood i Godfrey Hardy. Ten drugi był nazywany drugim wcieleniem Isaaca Newtona. Pomimo ich młodego wieku, matematycy mieli już na swoim koncie spore osiągnięcia, byli chwaleni i podziwiani szczególnie za oryginalne podejście do niektórych tematów. Można powiedzieć, że bardzo szybko zdobyli matematyczne szczyty, dlatego nie ma się co dziwić, że podnieśli rękawicę rzuconą przez Riemanna i postanowili udowodnić najtrudniejszą zagadkę matematyczną.

Jednak wbrew uprzednim zapowiedziom, Brytyjczycy ponieśli klęskę. Hardy'emu co prawda udało się dowieść, że na linii prostej znajduje się nieskończenie wiele miejsc zerowych, ale to dalej nie zmieniało faktu, że mogły znajdować się one także i poza nią. Pomimo licznych wysiłków i starań włożonych w udowodnienie Hipotezy Riemanna mężczyźni wciąż nie przedstawili żadnych jednoznacznych wyników. Efektem tego było ich zwątpienie w jej prawdziwość.

„Klątwa liczb pierwszych”

[Źródło]

Do największych ofiar zagadki liczb pierwszych należy John Nash, który w latach 50. XX w. uchodził za najwybitniejszego matematyka stulecia. Człowiek ten zdobył nawet nagrodę Nobla w dziedzinie ekonomii, złożył jednak swój wyjątkowy talent na ołtarzu Hipotezy Riemanna. Próbował on złamać kod liczb pierwszych, a z każdym dniem nadzieje na jego powodzenie rosły. Równo sto lat po ogłoszeniu przez niemieckiego matematyka swej słynnej hipotezy, miało nastąpić ogłoszenie wyników badań prof. Nasha. Wszyscy spodziewali się triumfu, genialnego umysłu, tymczasem to właśnie umysł poniósł największą porażkę. Nash zaczął nagle mówić od rzeczy, widoczne były u niego objawy schizofrenii. Zbyt intensywna praca intelektualna, której podejmował się matematyk sprawiła, że popadł on w chorobę psychiczną.

Wówczas najwybitniejsi naukowcy zaczęli odczuwać strach, rozpowszechniło się stwierdzenie, że hipoteza Riemanna z dnia na dzień potrafi zniszczyć karierę nawet najwybitniejszego matematyka. Nie obeszło się także bez głosów, że wszelkie podejmowane próby dotyczące udowodnienia Hipotezy Riemanna, spotykają się z gniewem Bożym. Tej kwestii rozstrzygać nie zamierzam, ale faktem jest, że wówczas wielu wybitnych matematyków, szerokim łukiem omijało liczby pierwsze.

„Nieoczeiwane spotkanie”

Do tego czasu wielu badaczy odżegnywało się od hipotezy Riemanna, tymczasem pewnego dnia w Instytucie Badań Zaawansowanych w New Jersey, penwne przypadkowe spotkanie położyło temu kres. Freeman Dyson- wybitny autorytet w dziedzinie fizyki cząstek elementarnych, któregoś dnia zrobił sobie przerwę na herbatę i podjął rozmowę z matematykiem- Hugh'iem Montgomery, który to zgłębiał tajemnice funkcji ζ. Montgomery wspomniał wówczas o miejscach zerowych funkcji Riemanna i wspomniał, że odkrył pewien związek między miejscami zerowymi- mianowicie że różnica między miejscami zerowymi wynosi:

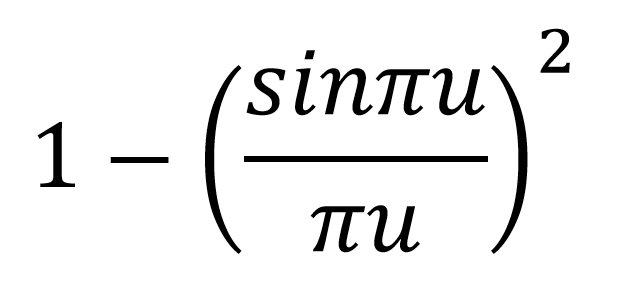
Dyson odparł wówczas, że taką samą postać ma funkcja rozkładów energetycznych jąder atomowych pierwiastków ciężkich. To przypadkowe spotaknie okazało się być prawdziwym przełomem. Jądro atomu, który jest podstawową cegiełką Wszechświata, określają poziomy energetyczne, które nie są stałe. Co warunkuje ich zmienność? Czy ma to związek z liczbami pierwszymi?

Okazało się, że odrębne dotychczas dziedziny wreszczie coś połączyło. To nowe odkrycie ponownie rozbudziło w matematykach- i nie tylko- zainteresowanie hipotezą Riemanna. Zdaniem niektórych badaczy wyjaśnienie tajemnicy liczb pierwszych pozwoli stworzyć tzw. "Teorię wszystkiego"- Boski wzorzec Wszechświata.

Czy uda nam się kiedyś złamać tajemniczy kod liczb pierwszych? Bardzo filozoficzne pytanie, na razie nikomu się to nie udało, chociaż w 2018 r. jeden z najbardziej szanowanych matematyków współczesnego świata, przedstawił na wykładzie, jak doszedł do udowodnienia Hipotezy Riemanna. Jeśli jego rozwiązanie uznane zostanie za poprawne, to Sir Michael Atiyah, za rozwiązanie jednego z 7 Problemów Milenijnych otrzyma milion dolarów. Co to będzie oznaczało dla świata? Czy rzeczywiście poznamy "Teorię wszystkiego"?