dr inż. Jerzy J. Jasielec

Pochodne, całki i metoda trapezów

PMiKNoM seminaria - zajęcia 2

Pochodne - rozwiązywanie analityczne

Zastosowanie pochodnych w inżynierii materiałowej i technologii chemicznej - przykłady.

Podstawowe wzory

`(x^n)'=n \cdot x^{n-1}` `(e^x)'=e^x` `(lnx)'=1/x` `(sinx)'=cosx` `(cosx)'=-sinx`

Pochodna iloczynu i ilorazu:

`(f \cdot g)'=f' \cdot g + g' \cdot f` `(f/g)'={f' \cdot g - g' \cdot f}/{g^2}`

Pochodna funkcji złożonej:

`(f(w(x)))'=f'(w(x)) \cdot w(x)'`

Zadania

Oblicz pochodne funkcji:

`f(x) = \sqrt{x} + 5x^2 + 3x + 1`
`f(x) = sin(x) \cdot ln(x)`
`f(x) = ln(2x+1)`
`f(x) = cos(-x^3 + 3x + 2)`
`f(x) = {x^2 + 2x}/sin(x)`

Wzór Taylora i pochodne numeryczne

Jeżeli funkcja `f` jest różniczkowalna w przedziale `(a,b)`, to dla każdego punktu `x` z tego przedziału spełniony jest tzw. wzór Taylora:

$$ f(x+h)=f(x)+ \frac{h}{1!} f^{(1)}(x)+ \frac {h^2}{2!} f^{(2)}(x) + \ldots + \frac {h^n}{n!} f^{(n)}(x)+R_{n}(x,a) $$

gdzie `f^{(k)}(x)` jest pochodną `k`-tego rzędu funkcji `f` obliczoną w punkcie `x`, a `R_{n}(x,a)` nazywana jest resztą Peano we wzorze Taylora.

Pierwsza pochodna lewo- i prawo-stronna

Dokonujemy Aproksymacji pierwszego rzędu, tj. zaniedbujemy wszystkie wyrazy ciągu Taylora, poza pierwszym. Wzór zapisany dla kroków `h` i `-h` wygląda następująco:

$$ f(x+h)=f(x)+ h \cdot f^{(1)}(x) \\ f(x-h)=f(x)- h \cdot f^{(1)}(x) $$

Po przekształceniu:

`f^{(1)}(x) = \frac {f(x+h) - f(x)}{h}` pochodna lewostronna

`f^{(1)}(x) = \frac {f(x) - f(x-h)}{h}` pochodna prawostronna

Pierwsza i druga pochodna centralna

Dokonujemy Aproksymacji drugiego rzędu, tj. zaniedbujemy wszystkie wyrazy ciągu Taylora, poza pierwszymi dwoma. Wzór zapisany dla kroków `h` i `-h` wygląda następująco:

$$ f(x+h)=f(x)+ h \cdot f^{(1)}(x)+ \frac {h^2}{2} f^{(2)}(x) \\ f(x-h)=f(x)- h \cdot f^{(1)}(x)+ \frac {h^2}{2} f^{(2)}(x) $$

Odemując drugi wzór od pierwszego otrzymujemy:

$$ f(x+h) - f(x-h) = 2 h \cdot f^{(1)}(x) $$

Po przekształceniu powstaje wzór na pierwszą pochodną centralną:

$$ f^{(1)}(x) = \frac {f(x+h) - f(x-h)}{2h} $$

Dodając oba wzory otrzymujemy:

$$ f(x+h) + f(x-h) = 2 \cdot f(x) + h^2 \cdot f^{(2)}(x) $$

Po przekształceniu powstaje wzór na drugą pochodną centralną:

$$ f^{(2)}(x) = \frac {f(x+h) -2 \cdot f(x)+ f(x-h)}{h^2} $$

Całki - rozwiązywanie analityczne

Zastosowanie całek w inżynierii materiałowej i technologii chemicznej - przykłady.

Podstawowe wzory

Jeżeli `f'(x)=g(x)` to `\int g(x)dx = f(x) + c`

`\int 0dx = 0 + c`

`\int 1dx = x + c`

`\int xdx = 1/2 x^2 + c`

`\int x^n dx = 1/{n+1} x^{n+1} + c`

`\int x^{-1}dx = ln \abs{x} + c`

`\int a^x dx = {a^x}/{ln(a)} + c \text{ dla } a>0`

`\int e^x dx = e^x + c`

`\int e^{kx} dx = 1/k e^{kx} + c`

`\int e^{-x} dx = -e^{-x} + c`

`\int sin x dx = -cos x + c`

`\int cos x dx = sin x + c`

Zadania

Oblicz następujące całki:

`\int(5x^4 - 3x^2 + 2/x + 1/{x^2}) dx = `
`\int(sin x - 2e^{-x} + 4^x) dx = `
`\int({2x^3 - 3^2 + 6x + 7}/{x^2}) dx = `
`\int(3^x - x^{-1} + cosx + 2) dx = `

Całki, których nie można rozwiązać analitycznie

`\int e^{-x^2} dx`

`\int sinx / x dx`

`\int x^x dx`

`\int 1/{ln(x)} dx`

Całki - rozwiązywanie numeryczne

Całka `\int_a^b f(x)` jest to pole powierzchni pod wykresem funkcji `f(x)` w przedziale `[a,b]`.

Interpretacja graficzna

Metoda Prostokątów

Aproksymacja funkcją stałą

Metoda Trapezów

Aproksymacja funkcją liniową

Metoda Simpsonów

Aproksymacja parabolą

_{* rysunki zaczerpnięte z Wikipedii, na licencji CC BY-SA 3.0. (Data dostępu 27.11.2017)}

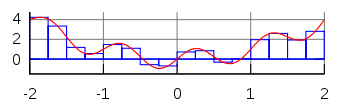
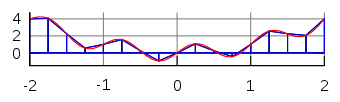
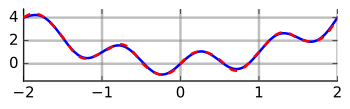
Rozwiązywanie całki metodą trapezów - wyprowadzenie

Wartość całki jest sumą pól powierzchni trapezów:

` calka = \sum_{i=0}^{n-1} ( h \cdot \frac {f(x_i)+f(x_{i+1})} 2 ) `

Rozwijamy sumę jednocześnie podmieniając `x_0=a` i `x_n=b` oraz wyciągając `h` przed nawias:

`c a l k a = h \cdot ( \frac {f(a)+f(x_1)} 2 `` + \frac {f(x_1)+f(x_2)} 2 `` + \frac {f(x_2)+f(x_3)} 2 `` + ... + \frac {f(x_{n-2})+f(x_{n-1})} 2 `` + \frac {f(x_{n-1})+f(b)} 2 ) `

Grupując odpowiednie wyrazy dochodzimy do wzoru:

` calka = h \cdot ( \frac {f(a)+f(b)} 2 + \sum_{i=1}^{n-1}f(x_i) ) `

Rozwiązywanie całek metodą trapezów - algorytm programu:

Zapisz definicję funkcji podcałkowej
Zadeklaruj zmienne
Pobierz zmienne `a`, `b` oraz `n` z arkusza kalkulacyjnego
Oblicz krok całkowania (wysokość trapezu)
Wyzeruj wartość zmiennej `s`
Oblicz sumę `s = \sum_{i=1}^{n-1}f(x_i)` - pętla for
Wylicz całkę (ze wzoru powyżej)
Wyświetl obliczoną wartość (jako MsgBox lub zapisz do arkusza)