Dr Jerzy J. Jasielec

Derivatives and integrals, trapezoidal rule

PMiKNoM seminars - class 2

Derivatives - analytical solutions

Application of derivatives in materials engineering and chemical technology - examples.

Basic equations

`(x^n)'=n \cdot x^{n-1}` `(e^x)'=e^x` `(lnx)'=1/x` `(sinx)'=cosx` `(cosx)'=-sinx`

Derivative of product and quotient:

`(f \cdot g)'=f' \cdot g + g' \cdot f` `(f/g)'={f' \cdot g - g' \cdot f}/{g^2}`

Derivative of embedded function:

`(f(w(x)))'=f'(w(x)) \cdot w(x)'`

Exercises

Calculate the derivatives of functions:

`f(x) = \sqrt{x} + 5x^2 + 3x + 1`
`f(x) = sin(x) \cdot ln(x)`
`f(x) = ln(2x+1)`
`f(x) = cos(-x^3 + 3x + 2)`
`f(x) = {x^2 + 2x}/sin(x)`

Taylor equation and numerical derivatives

If function `f` is differentiable in range `(a,b)`, than for every point `x` in this range, the condition known as Taylor equation is fullfilled:

$$ f(x+h)=f(x)+ \frac{h}{1!} f^{(1)}(x)+ \frac {h^2}{2!} f^{(2)}(x) + \ldots + \frac {h^n}{n!} f^{(n)}(x)+R_{n}(x,a) $$

where `f^{(k)}(x)` is the `k`-th order derivative of function `f`, calculated in point `x`, and `R_{n}(x,a)` is known as the Peano form of the remainder.

First left- and right-side derivative

We use the first order approximation, by neglecting all components of Taylor's polynomial, except the first one. The equation written for steps `h` i `-h`, takes the form:

$$ f(x+h)=f(x)+ h \cdot f^{(1)}(x) \\ f(x-h)=f(x)- h \cdot f^{(1)}(x) $$

After rearrangements:

`f^{(1)}(x) = \frac {f(x+h) - f(x)}{h}` left-side derivative

`f^{(1)}(x) = \frac {f(x) - f(x-h)}{h}` right-side derivative

First and second central derivative

We use the second order approximation, by neglecting all components of Taylor's polynomial, except the first two. The equation written for steps `h` i `-h`, takes the form:

$$ f(x+h)=f(x)+ h \cdot f^{(1)}(x)+ \frac {h^2}{2} f^{(2)}(x) \\ f(x-h)=f(x)- h \cdot f^{(1)}(x)+ \frac {h^2}{2} f^{(2)}(x) $$

After substracting the second equation from the first one, we obtain:

$$ f(x+h) - f(x-h) = 2 h \cdot f^{(1)}(x) $$

After rearrangements, one gets the equation for the first central derivative:

$$ f^{(1)}(x) = \frac {f(x+h) - f(x-h)}{2h} $$

After adding the equations, we obtain:

$$ f(x+h) + f(x-h) = 2 \cdot f(x) + h^2 \cdot f^{(2)}(x) $$

After rearrangements, one gets the equation for the second central derivative:

$$ f^{(2)}(x) = \frac {f(x+h) -2 \cdot f(x)+ f(x-h)}{h^2} $$

Integrals - analytical solutions

Application of integrals in materials engineering and chemical technology - examples.

Basic equations

If `f'(x)=g(x)` then `\int g(x)dx = f(x) + c`

`\int 0dx = 0 + c`

`\int 1dx = x + c`

`\int xdx = 1/2 x^2 + c`

`\int x^n dx = 1/{n+1} x^{n+1} + c`

`\int x^{-1}dx = ln \abs{x} + c`

`\int a^x dx = {a^x}/{ln(a)} + c \text{ dla } a>0`

`\int e^x dx = e^x + c`

`\int e^{kx} dx = 1/k e^{kx} + c`

`\int e^{-x} dx = -e^{-x} + c`

`\int sin x dx = -cos x + c`

`\int cos x dx = sin x + c`

Exercises

Calculate the following integrals:

`\int(5x^4 - 3x^2 + 2/x + 1/{x^2}) dx = `
`\int(sin x - 2e^{-x} + 4^x) dx = `
`\int({2x^3 - 3^2 + 6x + 7}/{x^2}) dx = `
`\int(3^x - x^{-1} + cosx + 2) dx = `

Integrals that cannot be solved analytically:

`\int e^{-x^2} dx`

`\int sinx / x dx`

`\int x^x dx`

`\int 1/{ln(x)} dx`

Integrals - numerical solutions

The integral `\int_a^b f(x)` is a surface area are under the plot of the `f(x)` functions with the limits `[a,b]`.

Graphical interpretation

Rectangle rule

Aproximation using a constant function

Trapezoidal rule

Aproximation using a linear function

Simpson's method

Aproximation using a parabola

_{* images above are taken from Wikipedia, based on CC BY-SA 3.0. licence. (access date 27 Nov 2017)}

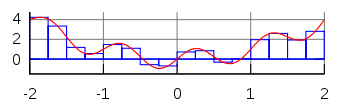
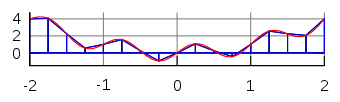
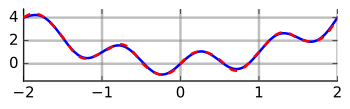
Solution of an integral using the trapezoidal rule - the equations

The value of an integral is a sum of the surface area of the trapezes:

`i n t e g r a l = \sum_{i=0}^{n-1} ( h \cdot \frac {f(x_i)+f(x_{i+1})} 2 ) `

We develop the sum, while substitutting `x_0=a` and `x_n=b`; and move `h` in front of the brackets:

`i n t e g r a l = h \cdot ( \frac {f(a)+f(x_1)} 2 `` + \frac {f(x_1)+f(x_2)} 2 `` + \frac {f(x_2)+f(x_3)} 2 `` + ... + \frac {f(x_{n-2})+f(x_{n-1})} 2 `` + \frac {f(x_{n-1})+f(b)} 2 ) `

After grouping the components of the sum we receive the final equation:

`i n t e g r a l = h \cdot ( \frac {f(a)+f(b)} 2 + \sum_{i=1}^{n-1}f(x_i) ) `

Solution of integrals using trapezoidal rule - program algorithm:

Define the itegrand function
Declare the variables
Read the values of variables `a`, `b` and `n` from the spreadsheet
Calculate the integration step (the height of the trapeze)
Assign zero to variable `s`
Calculate the sum `s = \sum_{i=1}^{n-1}f(x_i)` - for loop
Calculate the value of the integral (equation above)
Display the calculated value (as MsgBox or into the spreadsheet)