In [1]:

%plot inline -w 480 -h 480
format compact

Aproksymacja - plan centralny kompozycyjny¶

Belka jednostronnie utwierdzona¶

Dana jest belka o długości $L$ z materiału o module Younga $E$ posiadająca przekrój prostokątny o momencie bezwładności $I$ (wyznaczonym na podstawie jego szerokości $w$ i wysokości $h$). Równanie różniczkowe opisujące ugięcie belki utwierdzonej na jedmym końcu (dla $x=L$) z obciążeniem ciągłym $Q$ ma postać

\[\mathrm{EI}\,\frac{\partial ^4}{\partial x^4} y\left(x\right)=Q\]

Przemieszczenia maksymalne w belce występują na jej swobodnym końcu i wynoszą

\[\delta_{max} (w,h) =\frac{3\,L^4\,Q}{2 E\,h^3\,w}\]

Naprężenia maksymalne w belce występują na jej utwierdzonym końcu i wynoszą

\[\sigma_{max} (w,h) =\frac{3\,L^2\,Q}{h^2\,w}\]

Zakładając, że $L=1$ m, $E=2 \cdot 10^{11}$ Pa, $Q= 10^{5}$ N, oraz że $w$ i $h$ zawierają się w przedziale $[0.1, 0.2]$ m

Zapis pliku funkcyjnego opisującego model¶

In [2]:

%%file model_belki.m
function [delta_max sigma_max]=model_belki(w, h)
L=1;Q=1e5;E=1e11;
delta_max = (3*L^4*Q)/(2*E*h^3*w);
sigma_max = (3*L^2*Q)/(h^2*w);

Created file 'D:\Wprowadzenie_do_MATLAB\model_belki.m'.

In [3]:

[d s] = model_belki(0.1, 0.1)

d =
    0.0150
s =
   3.0000e+08

Eksperyment z planem centralnym kompozycyjnym pięciopoziomowym¶

In [4]:

clear all

% x_lim=[min(x_1) max(x_1)
%        min(x_2) max(x_2)]

x_lim=[.1 .2
       .1 .2]

x_lim =
    0.1000    0.2000
    0.1000    0.2000

In [5]:

x=ccdesign(2,'center',1, 'type','inscribed')

x =
   -0.7071   -0.7071
   -0.7071    0.7071
    0.7071   -0.7071
    0.7071    0.7071
   -1.0000         0
    1.0000         0
         0   -1.0000
         0    1.0000
         0         0

Skalowanie parametrów $ t_k $ z przedziału $ [-1, 1] $ do $ [x_{k,min}, x_{k,max}] $ na podstawie zależności

\[x_{k,exp} = \frac{x_{k,max}+x_{k,min}}{2} + x_{k} \frac{x_{k,max}-x_{k,min}}{2}\]

In [6]:

x_exp(:,1)=(x_lim(1,2)+x_lim(1,1))./2+x(:,1).*(x_lim(1,2)-x_lim(1,1))/2;
x_exp(:,2)=(x_lim(2,2)+x_lim(2,1))./2+x(:,2).*(x_lim(2,2)-x_lim(2,1))/2;
x_exp

x_exp =
    0.1146    0.1146
    0.1146    0.1854
    0.1854    0.1146
    0.1854    0.1854
    0.1000    0.1500
    0.2000    0.1500
    0.1500    0.1000
    0.1500    0.2000
    0.1500    0.1500

In [7]:

for k=1:length(x(:,1))
[d s]=model_belki(x_exp(k,1), x_exp(k,2));
y(k,1)=s;
end
y

In [8]:

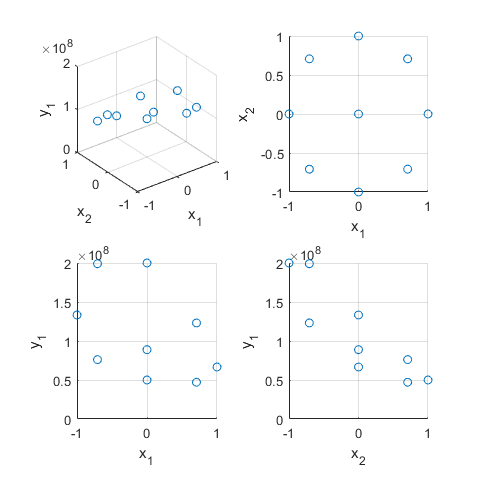
subplot(2,2,1)
plot3(x(:,1),x(:,2),y(:,1),'o'), xlabel('x_1'), ylabel('x_2'), zlabel('y_1'), grid on, view(3)
subplot(2,2,2)
plot3(x(:,1),x(:,2),y(:,1),'o'), xlabel('x_1'), ylabel('x_2'), zlabel('y_1'), grid on, view(0,90)
subplot(2,2,3)
plot3(x(:,1),x(:,2),y(:,1),'o'), xlabel('x_1'), ylabel('x_2'), zlabel('y_1'), grid on, view(0,0)
subplot(2,2,4)
plot3(x(:,1),x(:,2),y(:,1),'o'), xlabel('x_1'), ylabel('x_2'), zlabel('y_1'), grid on, view(90,0)

Aproksymacja punktów powierzchnią odpowiedzi¶

In [9]:

%Założenie postaci funkcji
%f1(x1,x2) = a00+a10*x1+a01*x2+a20*x1^2+a02*x2^2
%funkcje bazowe
X=[ones(length(x(:,1)),1) x(:,1) x(:,2) x(:,1).*x(:,2) x(:,1).^2 x(:,2).^2]

Y=y(:,1);
%XA=Y
A=X\Y

a00=A(1);a10=A(2);a01=A(3);a11=A(4);a20=A(5);a02=A(6);

f1=@(x1,x2) a00+a10*x1+a01*x2+a11*x1.*x2+a20*x1.^2+a02*x2.^2

[X1,X2]=meshgrid([-1:0.25:1]);
Y1=f1(X1,X2);

X =
    1.0000   -0.7071   -0.7071    0.5000    0.5000    0.5000
    1.0000   -0.7071    0.7071   -0.5000    0.5000    0.5000
    1.0000    0.7071   -0.7071   -0.5000    0.5000    0.5000
    1.0000    0.7071    0.7071    0.5000    0.5000    0.5000
    1.0000   -1.0000         0         0    1.0000         0
    1.0000    1.0000         0         0    1.0000         0
    1.0000         0   -1.0000         0         0    1.0000
    1.0000         0    1.0000         0         0    1.0000
    1.0000         0         0         0         0         0
A =
   1.0e+07 *
    8.8889
   -3.5230
   -7.2672
    2.3448
    1.0550
    3.5550
f1 =
  function_handle with value:
    @(x1,x2)a00+a10*x1+a01*x2+a11*x1.*x2+a20*x1.^2+a02*x2.^2

In [10]:

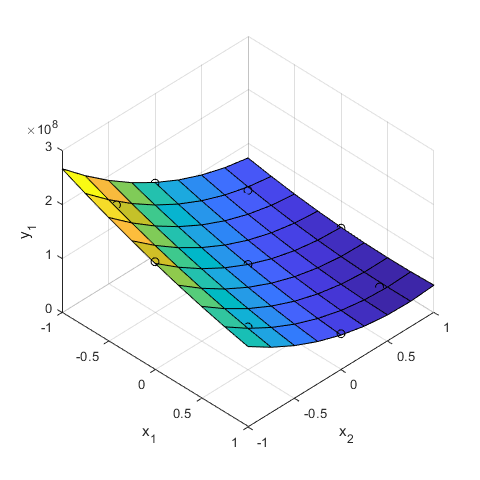
surf(X1,X2,Y1)
hold on
plot3(x(:,1),x(:,2),y(:,1),'ok')
xlabel('x_1'), ylabel('x_2'), zlabel('y_1')
view(45,45)
grid on