In [1]:
format compact
Optymalizacja¶
Przykłady zaczerpnięte z książki
K.-H. Chang, Design Theory and Methods using CAD/CAE. Academic Press, 2014
Puszka na piwo (funkcja jednej zmiennej)¶
Przy założeniu, że model geometryczny puszki jest walcem o promieniu \(r\) i wysokości \(h\), poszukiwana jest maksymalna objętość \(V(r,h)\) przy zadanej powierzchni \(A_0\).
Maksymalizacja: \(V(r,h)=\pi r^2 h\) Przy ograniczeniach: \(A(r,h)=\pi r(r+2h)=A_0,~~r>0,~~h>0\)
Czyli poszukiwane jest maksimum funkcji
\[V(h) = \pi \,h\,{\left(-h+\sqrt{h^2+\frac{A_0}{\pi}}\right)}^2\]
Zakładając, że \(A_0=4 \pi\)
\[V(h) = \pi \,h\,{\left(-h+\sqrt{h^2+4}\right)}^2\]
Rozwiązanie analityczne¶
In [2]:
clear all
syms h r A_0
In [3]:
A0=4*pi;
V=pi*h.*(-h+(h.^2+(A0/pi)).^0.5).^2
pretty(V)
V =
h*pi*(h - (h^2 + 4)^(1/2))^2
2 2
h pi (h - sqrt(h + 4))
In [4]:
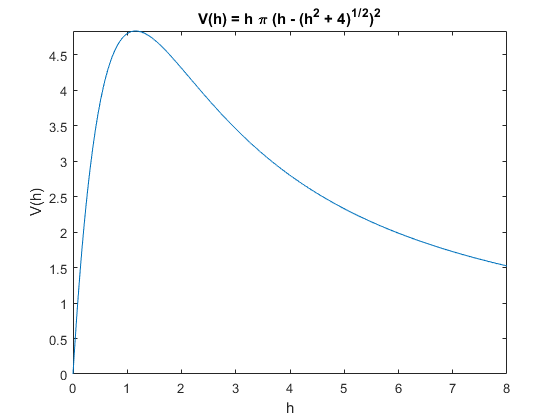
fplot(V,[0 8]) % lub ezplot()
title(['V(h) = ' texlabel(V)])
xlabel('h'),ylabel('V(h)')
In [5]:
gradV=gradient(V,h) %dla jednego wymiaru równoważny z "diff()"
gradV =
pi*(h - (h^2 + 4)^(1/2))^2 - 2*h*pi*(h - (h^2 + 4)^(1/2))*(h/(h^2 + 4)^(1/2) - 1)
In [6]:
h_ext=solve(gradV==0)
h_ext =
(2*3^(1/2))/3
In [7]:
Rozwiazanie=double(h_ext)
Rozwiazanie =
1.1547
In [8]:
H=diff(gradV) %druga pochodna
H =
2*h*pi*(h/(h^2 + 4)^(1/2) - 1)^2 - 4*pi*(h - (h^2 + 4)^(1/2))*(h/(h^2 + 4)^(1/2) - 1) - 2*h*pi*(1/(h^2 + 4)^(1/2) - h^2/(h^2 + 4)^(3/2))*(h - (h^2 + 4)^(1/2))
In [9]:
subs(H,h_ext) %podstawienie
ans =
-(pi*3^(1/2))/2
In [10]:
double(ans)
ans =
-2.7207
Jeżeli pierwsza pochodna funkcji w punkcie \(h_{ext}\) jest równa 0 a druga pochodna funkcji ujemna to jest to maksimum
Rozwiązanie numeryczne¶
In [11]:
clear all
h=0:0.1:8;
A0=pi;
V=pi*h.*(-h+(h.^2+4*A0/pi).^0.5).^2;
In [12]:
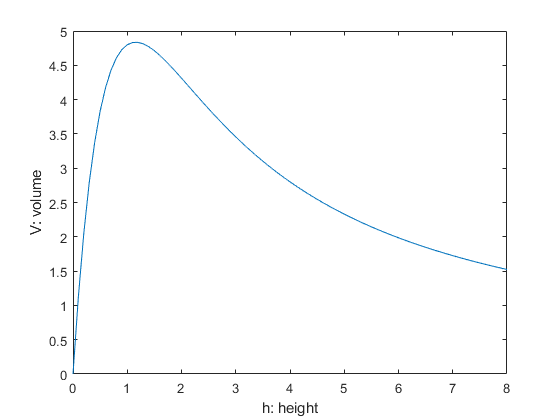
plot(h,V);
xlabel('h: height'); ylabel('V: volume');
In [13]:
f=@(h)-(pi*h.*(-h+(h.^2+4*A0/pi).^0.5).^2)
f =
function_handle with value:
@(h)-(pi*h.*(-h+(h.^2+4*A0/pi).^0.5).^2)
In [14]:
h_max=fminsearch(f,0)
h_max =
1.1547
Funkcja dwu zmiennnych¶
Poszukiwane są ekstrema funkcji
\[f(x_1,x_2)=x_{2}\,{\mathrm{e}}^{-{x_{1}}^2-{x_{2}}^2}\]
w przedziale \([-2, 2]\)
Rozwiązanie analityczne¶
In [15]:
syms x_1 x_2
f=x_2*exp(-x_1^2-x_2^2);
pretty(f)
2 2
x_2 exp(- x_1 - x_2 )
In [16]:
fsurf(f,[-2,2])
title(['f(x,y,z) = ' texlabel(f)])
xlabel('x_1'), ylabel('x_2'), zlabel('f(x_1,x_2)')
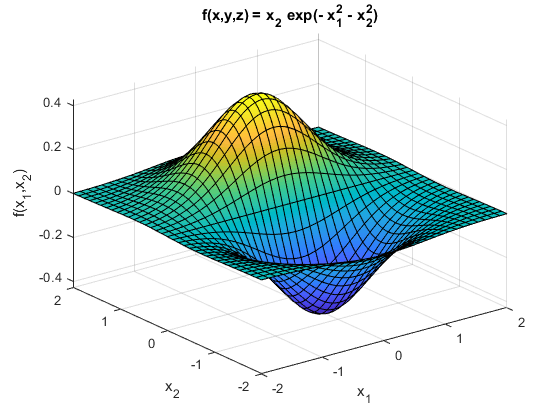
Gradient \(\nabla f\)
In [17]:
gradf=gradient(f)
gradf =
-2*x_1*x_2*exp(- x_1^2 - x_2^2)
exp(- x_1^2 - x_2^2) - 2*x_2^2*exp(- x_1^2 - x_2^2)
In [18]:
pretty(gradf)
/ 2 2 \
| -2 x_1 x_2 exp(- x_1 - x_2 ) |
| |
| 2 2 2 2 2 |
\ exp(- x_1 - x_2 ) - 2 x_2 exp(- x_1 - x_2 ) /
In [19]:
extrem=solve(gradf==0)
extrem =
struct with fields:
x_1: [2x1 sym]
x_2: [2x1 sym]
In [20]:
x=double([extrem.x_1(1) extrem.x_2(1)])
x =
0 -0.7071
In [21]:
x=[x; double([extrem.x_1(2) extrem.x_2(2)])]
x =
0 -0.7071
0 0.7071
Hessian \(\mathbf{H} = \nabla^2 f\)
In [22]:
H=jacobian(gradf, [x_1, x_2])
H =
[ 4*x_1^2*x_2*exp(- x_1^2 - x_2^2) - 2*x_2*exp(- x_1^2 - x_2^2), 4*x_1*x_2^2*exp(- x_1^2 - x_2^2) - 2*x_1*exp(- x_1^2 - x_2^2)]
[ 4*x_1*x_2^2*exp(- x_1^2 - x_2^2) - 2*x_1*exp(- x_1^2 - x_2^2), 4*x_2^3*exp(- x_1^2 - x_2^2) - 6*x_2*exp(- x_1^2 - x_2^2)]
In [23]:
H=hessian(f,[x_1,x_2])
H =
[ 4*x_1^2*x_2*exp(- x_1^2 - x_2^2) - 2*x_2*exp(- x_1^2 - x_2^2), 4*x_1*x_2^2*exp(- x_1^2 - x_2^2) - 2*x_1*exp(- x_1^2 - x_2^2)]
[ 4*x_1*x_2^2*exp(- x_1^2 - x_2^2) - 2*x_1*exp(- x_1^2 - x_2^2), 4*x_2^3*exp(- x_1^2 - x_2^2) - 6*x_2*exp(- x_1^2 - x_2^2)]
In [24]:
H_1=double(subs(H, [x_1 x_2], [x(1,1), x(1,2)]))
H_2=double(subs(H, [x_1 x_2], [x(2,1), x(2,2)]))
H_1 =
0.8578 0
0 1.7155
H_2 =
-0.8578 0
0 -1.7155
In [25]:
detH_1=det(H_1),detH_2=det(H_2)
detH_1 =
1.4715
detH_2 =
1.4715
Funkcja \(f\) ma ekstremum gdy \(\nabla f = 0\) oraz wyznacznik hessianu H jest dodatni. Gdy H > 0 jest to minimum, a gdy H < 0 to maksimum.
Rozwiązanie numeryczne¶
In [26]:
clear x
clear f
In [27]:
f=@(x) x(2)*exp(-x(1)^2-x(2)^2)
f =
function_handle with value:
@(x)x(2)*exp(-x(1)^2-x(2)^2)
In [28]:
x_min=fminsearch(f,[0 0])
g=@(x)-f(x)
x_max=fminsearch(g,[0 0])
x_min =
0.0000 -0.7071
g =
function_handle with value:
@(x)-f(x)
x_max =
0.0000 0.7071