In [1]:

%plot inline -w 720

Podstawy¶

Przykłady są dla MATLAB 2017b (jeśli funkcje są inne dla MATLAB 2014a to zaznaczono to w komentarzach)

Macierze i wektory¶

In [2]:

clear all % usunięcie zmiennych z pamięci
format compact

In [3]:

X=[1 2 3; 4 5 6]  % wprowadzenie macierzy

X =
     1     2     3
     4     5     6

In [4]:

X(3,4)=8           % wprowaczenie wartości elementu w wierszu i kolumnie

X =
     1     2     3     0
     4     5     6     0
     0     0     0     8

In [5]:

X(3,1:2)=9          % wprowaczenie wartości elementu w wierszu i kolumnach

X =
     1     2     3     0
     4     5     6     0
     9     9     0     8

In [6]:

X(2,:)=7            % wprowaczenie wartości elementu w wierszu i całej kolumnie

X =
     1     2     3     0
     7     7     7     7
     9     9     0     8

In [7]:

Z=zeros(4)  % stworzenie kwadratowej macierzy zer, analogicznie działa funkcja "ones", "eye"

Z =
     0     0     0     0
     0     0     0     0
     0     0     0     0
     0     0     0     0

In [8]:

O=ones(4,2)      % stworzenie macierzy jedynek o wymiarach 4 na 2

In [9]:

R=rand(3,6)     % stworzenie macierzy liczb pseudolosowych z przedziału [0, 1]

R =
    0.8147    0.9134    0.2785    0.9649    0.9572    0.1419
    0.9058    0.6324    0.5469    0.1576    0.4854    0.4218
    0.1270    0.0975    0.9575    0.9706    0.8003    0.9157

In [10]:

x=X(1,3)          % odczyt wartości elementu w wierszu i kolumnie

x =
     3

In [11]:

A=X(1,:)          % odczyt wartości wszystkich elementów w pierwszym wierszu

A =
     1     2     3     0

In [12]:

x=0:6             % stworzenie wektora z liczb całkowitych od 0 do 6

x =
     0     1     2     3     4     5     6

Wykres funkcji¶

plot (MATLAB Documentation)

In [13]:

x=0:0.5:6         % stworzenie wektora z krokiem 0.5

x =
         0    0.5000    1.0000    1.5000    2.0000    2.5000    3.0000    3.5000    4.0000    4.5000    5.0000    5.5000    6.0000

In [14]:

y=x.^2            % wpisanie wzoru (.^ - operator działań na tablicach)

y =
         0    0.2500    1.0000    2.2500    4.0000    6.2500    9.0000   12.2500   16.0000   20.2500   25.0000   30.2500   36.0000

In [15]:

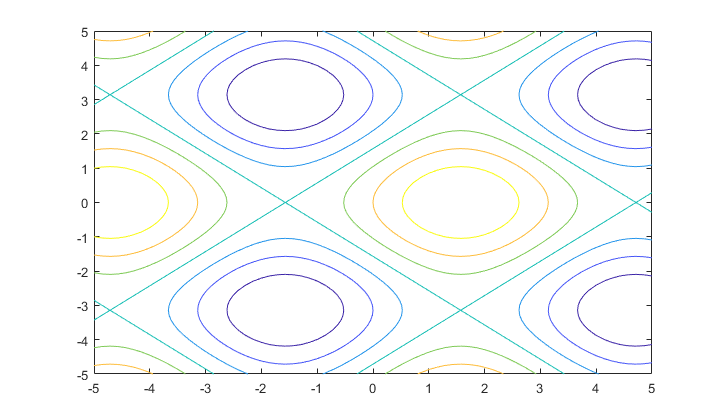
plot(x,y,'o-'); xlabel('x'); ylabel('y')

Wykorzystanie funkcji anonimowej \(f(x)\):

In [16]:

f=@(x) x.^2        % zdefiniowanie funkcji f

f =
  function_handle with value:
    @(x)x.^2

In [17]:

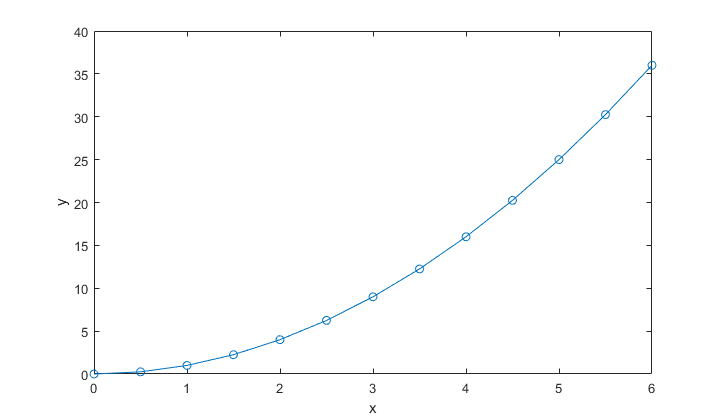
plot(x,f(x),'.-'); xlabel('x'); ylabel('y')

In [18]:

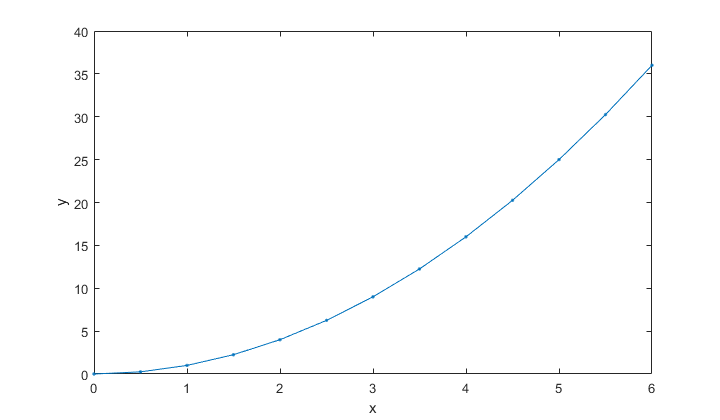
[X,Y] = meshgrid(-2:0.2:2,-2:0.2:2);
Z = X.*exp(-X.^2 - Y.^2);
figure
surface(X,Y,Z)
grid on
view(3)

In [19]:

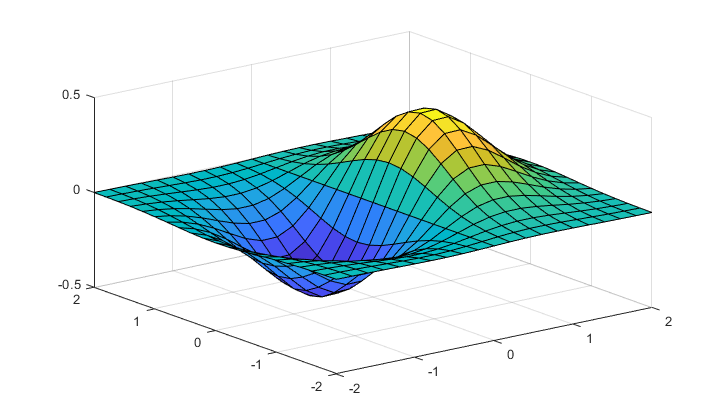
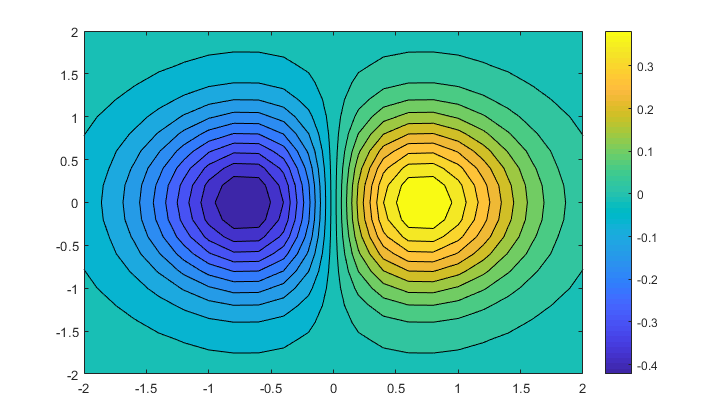
contourf(X,Y,Z, 20)      % wykres konturowy
colorbar

Anonimowe funkcje i ich wykorzystanie¶

Anonymous functions (MATLAB Documentation)

Definicja funkcji \(h(x) = {g} \cdot {x}\) :

In [20]:

g = 10;
h = @(x) g*x;

Definicja funkcji \(f(x)=sin(\alpha x)\) :

In [21]:

alpha = 0.8;
f = @(x) sin(alpha*x);

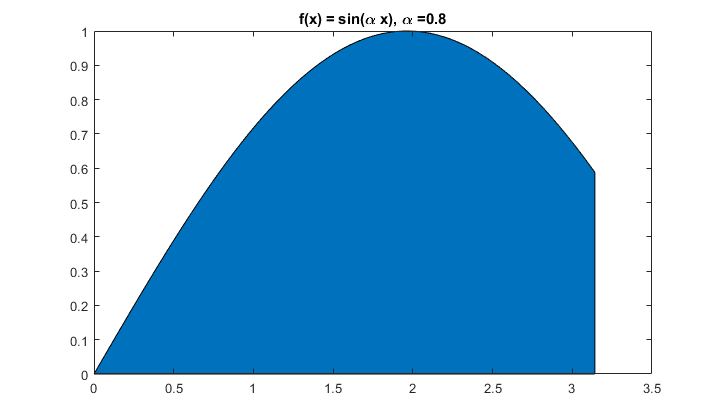
Wykres funkcji z zaznaczoną powierzchnią pod nim:

In [22]:

x = 0:pi/100:pi;
area(x,f(x)); % You can evaluate f without feval
title(['f(x) = sin(\alpha x), \alpha =' num2str(alpha)]);

Numeryczne wyznaczenie wartości całki oznaczonej \(\int_0^\pi sin(\alpha x)\) przy pomocy funckcji quad:

In [23]:

I=quad(f,0,pi)

I =
    2.2613

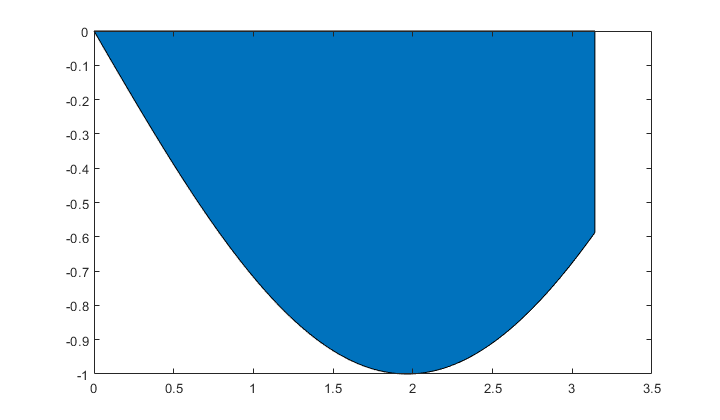
Wyznaczenie maksimum funkcji \(sin(\alpha x)\) w przedziale \([0,\pi]\) przy pomocy funkcji fminsearch:

In [24]:

f2=@(x)-f(x);
area(x,f2(x))

In [25]:

x_ext = fminsearch(f2,0)

x_ext =
    1.9635

Wyznaczenie miejsca zerowego funkcji \(f(x)=x-cos(x)\) :

In [26]:

fun=@(x)x-cos(x)
x_z=fzero(fun,1)        %punkt początkowy x_0=1

fun =
  function_handle with value:
    @(x)x-cos(x)
x_z =
    0.7391

Rozwiązanie układu równań¶

Rozwiązanie układu równań ( mldivide ) :

\[\begin{split}\begin{eqnarray} 4a_1 + 2a_2 + a_3 = 2 \\ 2a_1 + a_2 + a_3= 4 \\ a_1 + 6a_2 + a_3 = 0 \\ \end{eqnarray}\end{split}\]

In [27]:

%Xa=Y
X=[4 2 1
   2 1 1
   1 6 1]
Y=[2 4 0].'

a=X\Y

X =
     4     2     1
     2     1     1
     1     6     1
Y =
     2
     4
     0
a =
   -0.5455
   -0.9091
    6.0000

Pętle i instrukcje warunkowe¶

Pętla while :

In [28]:

c=3
while c>0
c=c-1;
disp(c)
end

Pętla for :

In [29]:

for c=3:-1:0
disp(c)
end

Instrukcja warunkowa if :

In [30]:

x=2
if x > 0
       disp('x is positive')
   elseif x<0
       disp('x is negative')
   else
       disp('x is 0')
end

x =
     2
x is positive

Obliczenia symboliczne¶

Symbolic Math Toolbox

Wyznaczanie wzoru pochodnej lub całki:

In [31]:

syms x

In [32]:

diff(2*x^2)           % wyznaczenie wzoru pochodnej

ans =
4*x

In [33]:

I_s=int(2*x^2)         % wyznaczenie wzoru całki

I_s =
(2*x^3)/3

In [34]:

I_s=int(2*x^2, 0, 2)   % całkowanie w granicach [0, 2]

I_s =
16/3

In [35]:

double(I_s)             % zamiana ze zmiennej symbolicznej na "double"

ans =
    5.3333

In [36]:

syms a b y(x)
dsolve(diff(y) == -a*y)           % rozwiązanie ogólne równania

ans =
C1*exp(-a*x)

In [37]:

dsolve(diff(y) == -a*y, y(0)==b)  % z uwzględnieniem warunku początkowego

ans =
b*exp(-a*x)

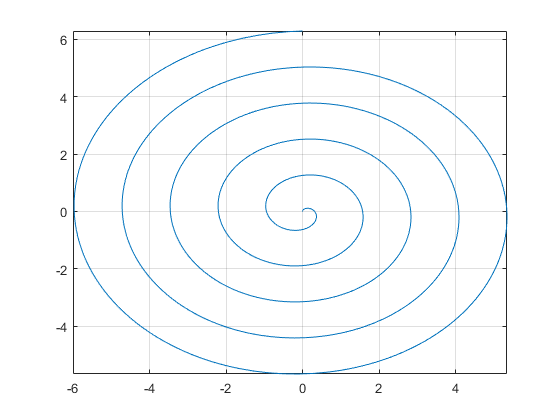
Rysowanie wykresów:

In [2]:

syms t
x = t*sin(5*t);
y = t*cos(5*t);
fplot(x, y, [0 2*pi])    % dla wersji 2014a analogiczny wykres rysuje 'ezplot'
grid on

In [39]:

syms x y
fsurf(sin(x) + cos(y))   % dla wersji 2014a analogiczny wykres rysuje 'ezsurf'

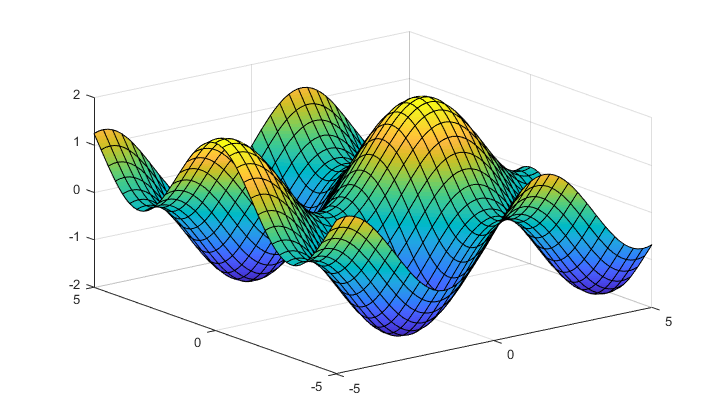
In [40]:

fcontour(sin(x) + cos(y))    % dla wersji 2014a analogiczny wykres rysuje 'ezcontour'