In [1]:

%plot inline -w 740

Wizualizacja wielowymiarowych danych¶

(Visualizing Multivariate Data - MATLAB documentation)

„In this example, we’ll use the carbig dataset, a dataset that contains various measured variables for about 400 automobiles from the 1970’s and 1980’s. We’ll illustrate multivariate visualization using the values for fuel efficiency (in miles per gallon, MPG), acceleration (time from 0-60MPH in sec), engine displacement (in cubic inches), weight, and horsepower. We’ll use the number of cylinders to group observations.”

In [2]:

clear all       % usunięcie zmiennych z pamięci
close all       % zamknięcie okien graficznych
format compact  % wyświetlanie wyników bez dodatkowych pustych linii

Wczytanie danych¶

In [3]:

load carbig
X = [MPG,Acceleration,Displacement,Weight,Horsepower];
varNames = {'MPG'; 'Acceleration'; 'Displacement'; 'Weight'; 'Horsepower'};

In [4]:

disp('X:'),disp(X(1:6,:)),disp(' ')
disp('Size of X:'), disp(size(X)),disp(' ')
disp('Model:'),disp(Model(1:6,:)),disp(' ')
disp('Cylinders:'),disp(Cylinders(1:6,:)),disp(' ')
disp('Min max:'), disp([min(Cylinders), max(Cylinders)])

X:
   1.0e+03 *
    0.0180    0.0120    0.3070    3.5040    0.1300
    0.0150    0.0115    0.3500    3.6930    0.1650
    0.0180    0.0110    0.3180    3.4360    0.1500
    0.0160    0.0120    0.3040    3.4330    0.1500
    0.0170    0.0105    0.3020    3.4490    0.1400
    0.0150    0.0100    0.4290    4.3410    0.1980

Size of X:
   406     5

Model:
chevrolet chevelle malibu
buick skylark 320
plymouth satellite
amc rebel sst
ford torino
ford galaxie 500

Cylinders:
     8
     8
     8
     8
     8
     8

Min max:
     3     8

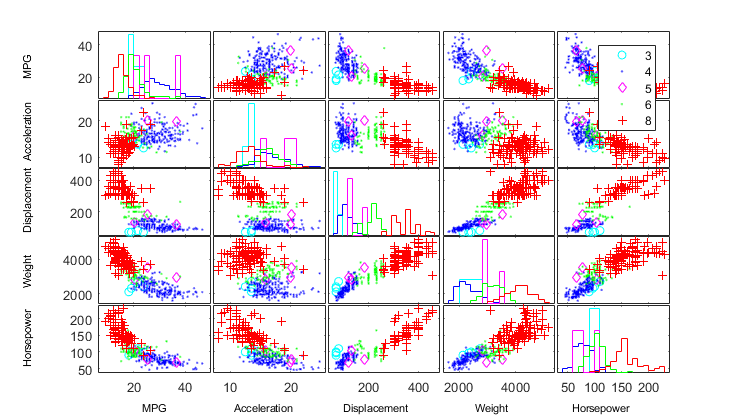
Wykresy rozrzutu¶

In [5]:

figure
plt=gplotmatrix(X,[],Cylinders,['c' 'b' 'm' 'g' 'r'],['o.d.+'],[],'on');
text([.08 .24 .43 .66 .83], repmat(-.1,1,5), varNames, 'FontSize',8);
text(repmat(-.12,1,5), [.86 .62 .41 .25 .02], varNames, 'FontSize',8, 'Rotation',90);
%set(plt,{'markers'},{12;5;9;9;9})
h = findobj(plt,'Tag','legend');
set(h, 'String', {'3', '4', '5', '6', '8'}, 'position',[.87 .8 0.06 0.16])

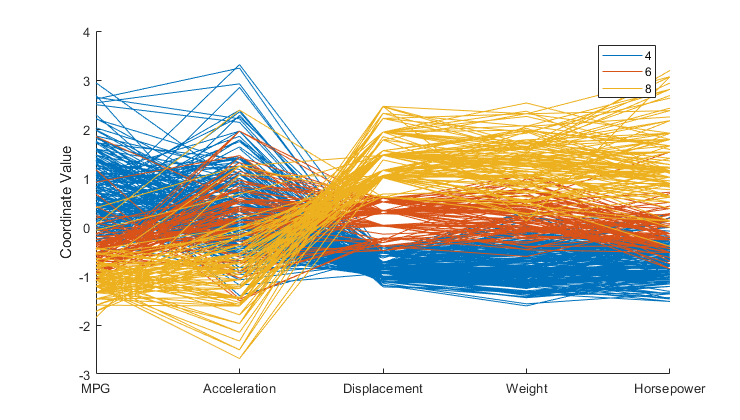
Wykres współrzędnych równoległych¶

(parallel coordinates plot)

In [6]:

Cyl468 = ismember(Cylinders,[4 6 8]);
parallelcoords(X(Cyl468,:), 'group',Cylinders(Cyl468), ...      %wartości na osi pionowej są ustandaryzowane
               'standardize','on', 'labels',varNames)           %każda zmienna ma wartość średnią 0 i wariancję 1

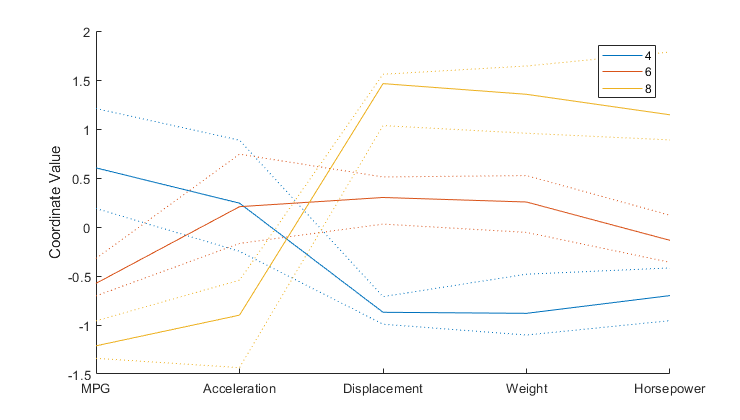
In [7]:

parallelcoords(X(Cyl468,:), 'group',Cylinders(Cyl468), ...
               'standardize','on', 'labels',varNames, 'quantile',.25)

Wykres glifów¶

(glyph plot)

In [8]:

h = glyphplot(X(1:9,:), 'glyph','star', 'varLabels',varNames, 'obslabels',Model(1:9,:));
set(h(:,3),'FontSize',8);

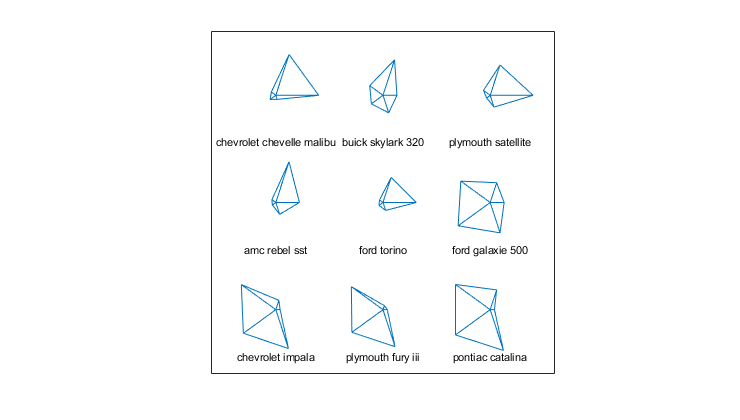
A star plot represents each observation as a “star” whose i-th spoke is proportional in length to the i-th coordinate of that observation

In [9]:

h = glyphplot(X(1:9,:), 'glyph','face', 'varLabels',varNames, 'obslabels',Model(1:9,:));
set(h(:,3),'FontSize',8);

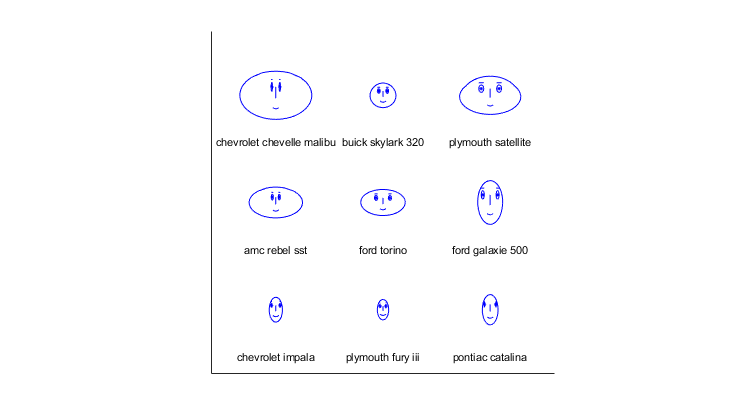
Column Facial Feature:

No.	Feature	Parameter
1	Size of face	«MPG»
2	Forehead/jaw relative arc length	«Acceleration»
3	Shape of forehead	«Displacement»
4	Shape of jaw	«Weight»
5	Width between eyes	«Horsepower»
6	Vertical position of eyes

In [10]:

models77 = find((Model_Year==77))

In [11]:

s=size(models77)
l=length(models77)

In [12]:

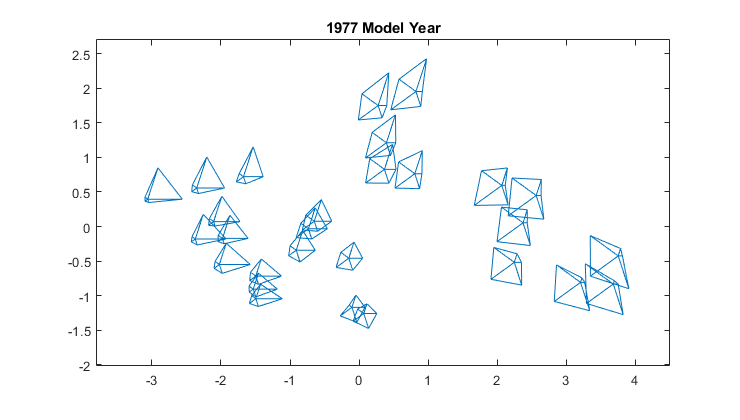
h = glyphplot(X(models77,:), 'glyph', 'star' , 'grid',[5 6], 'varLabels', varNames,...
'obslabels', Model(models77,1:10));
set(h(:,3),'FontSize',8);

In [13]:

zs=zscore(X(models77,:));
dissimilarity = pdist(zs);

In [14]:

Y = mdscale(dissimilarity,2);
glyphplot(X(models77,:), 'glyph','star', 'centers',Y, ...
          'varLabels',varNames, 'obslabels',Model(models77,:), 'radius',.5);
title('1977 Model Year');