In [1]:
%plot inline -w 480 -h 480
format compact
Planowanie eksperymentu¶
Przykłady są dla MATLAB 2025a (jeśli funkcje są inne dla MATLAB 2014a to zaznaczono to w komentarzach)
Generowanie planu eksperymentu¶
Plan dwupoziomowy¶
In [2]:
help ff2n
FF2N Two-level full-factorial design.
X = FF2N(N) creates a two-level full-factorial design, X.
N is the number of columns of X. The number of rows is 2^N.
Reference page in Doc Center
doc ff2n
In [3]:
dFF2 = ff2n(2)
[s,~]=size(dFF2)
dFF2 =
0 0
0 1
1 0
1 1
s =
4
In [4]:
dFF2 = ff2n(3)
[s,~]=size(dFF2)
dFF2 =
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
s =
8
In [5]:
help fullfact
FULLFACT Mixed-level full-factorial designs.
DESIGN=FULLFACT(LEVELS) creates a matrix DESIGN containing the
factor settings for a full factorial design. The vector LEVELS
specifies the number of unique settings in each column of the design.
Example:
LEVELS = [2 4 3];
DESIGN = FULLFACT(LEVELS);
This generates a 24 run design with 2 levels in the first column,
4 in the second column, and 3 in the third column.
Reference page in Doc Center
doc fullfact
In [6]:
dFF=fullfact([2 2])
dFF =
1 1
2 1
1 2
2 2
In [7]:
plot(dFF(:,1),dFF(:,2),'o')
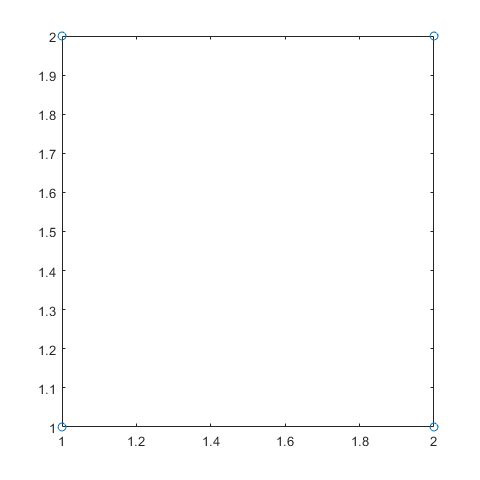
In [8]:
dFF3=fullfact([2 2 2])
dFF3 =
1 1 1
2 1 1
1 2 1
2 2 1
1 1 2
2 1 2
1 2 2
2 2 2
In [9]:
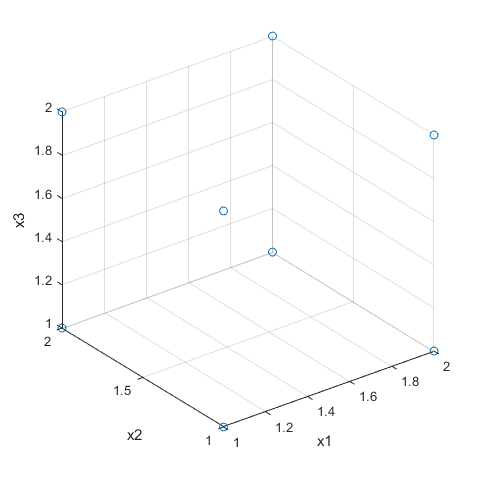
plot3(dFF3(:,1),dFF3(:,2),dFF3(:,3),'o'), grid on
xlabel('x1'),ylabel('x2'),zlabel('x3')
view(3)
In [10]:
help fracfact
FRACFACT Fractional factorial design for two-level factors.
X = FRACFACT(GEN) produces the fractional factorial design defined by
the generator string GEN. GEN must be a sequence of "words" separated
by spaces. If the generator string consists of P words using K letters
of the alphabet, then X has N=2^K rows and P columns. Each word
defines how the corresponding factor's levels are defined as products
of generators from a 2^K full-factorial design. Alternatively, GEN can
be a cell array of strings, with one word per cell.
[X, CONF] = FRACFACT(GEN) also returns CONF, a cell array of
strings containing the confounding pattern for the design.
[...] = FRACFACT(GEN, 'PARAM1',val1, 'PARAM2',val2,...) specifies one
or more of the following name/value pairs:
'MaxInt' Maximum level of interaction to include in the
confounding output (default 2)
'FactorNames' Cell array specifying the name for each factor
(default names are X1, X2, ...)
Example:
x = fracfact('a b c abc')
produces an 8-run fractional factorial design for four variables, where
the first three columns are an 8-run 2-level full factorial design for
the first three variables, and the fourth column is the product of the
first three columns. The fourth column is confounded with the
three-way interaction of the first three columns.
See also FF2N, FULLFACT, FRACFACTGEN.
Reference page in Doc Center
doc fracfact
In [11]:
[dfF3,confounding] = fracfact('a b ab')
dfF3 =
-1 -1 1
-1 1 -1
1 -1 -1
1 1 1
confounding =
7x3 cell array
{'Term' } {'Generator'} {'Confounding'}
{'X1' } {'a' } {'X1 + X2*X3' }
{'X2' } {'b' } {'X2 + X1*X3' }
{'X3' } {'ab' } {'X3 + X1*X2' }
{'X1*X2'} {'ab' } {'X3 + X1*X2' }
{'X1*X3'} {'b' } {'X2 + X1*X3' }
{'X2*X3'} {'a' } {'X1 + X2*X3' }
In [12]:
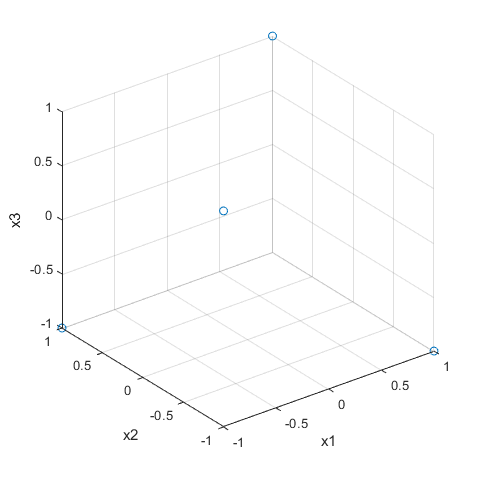
plot3(dfF3(:,1),dfF3(:,2),dfF3(:,3),'o'), grid on
xlabel('x1'),ylabel('x2'),zlabel('x3')
view(3)
Plan trójpoziomowy i pięciopoziomowy¶
In [13]:
help bbdesign
BBDESIGN Generate Box-Behnken design.
D=BBDESIGN(NFACTORS) generates a Box-Behnken design for NFACTORS
factors. The output matrix D is N-by-NFACTORS, where N is the
number of points in the design. Each row lists the settings for
all factors, scaled between -1 and 1.
D=BBDESIGN(NFACTORS,'PNAME1',pvalue1,'PNAME2',pvalue2,...)
allows you to specify additional parameters and their values.
Valid parameters are the following:
Parameter Value
'center' The number of center points to include.
'blocksize' The maximum number of points allowed in a block.
[D,BLK]=BBDESIGN(...) requests a blocked design. The output
vector BLK is a vector of block numbers.
Box and Behnken proposed designs when the number of factors was
equal to 3-7, 9-12, or 16. This function produces those designs.
For other values of NFACTORS, this function produces designs
that are constructed in a similar way, even though they were not
tabulated by Box and Behnken and they may be too large to be
practical.
See also CCDESIGN, ROWEXCH, CORDEXCH.
Reference page in Doc Center
doc bbdesign
In [14]:
dBB = bbdesign(3)
dBB =
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
0 1 -1
0 1 1
0 0 0
0 0 0
0 0 0
In [15]:
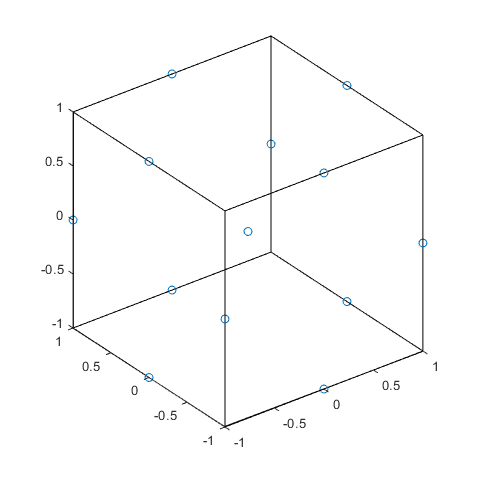
plot3(dBB(:,1),dBB(:,2),dBB(:,3),'o')
X = [1 -1 -1 -1 1 -1 -1 -1 1 1 -1 -1;
1 1 1 -1 1 1 1 -1 1 1 -1 -1];
Y = [-1 -1 1 -1 -1 -1 1 -1 1 -1 1 -1;
1 -1 1 1 1 -1 1 1 1 -1 1 -1];
Z = [1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1;
1 1 1 1 -1 -1 -1 -1 1 1 1 1];
line(X,Y,Z,'Color','k')
axis square equal
In [16]:
help ccdesign
CCDESIGN Generate central composite design.
D=CCDESIGN(NFACTORS) generates a central composite design for
NFACTORS factors. The output matrix D is N-by-NFACTORS, where N is
the number of points in the design. Each row represents one run of
the design, and it has the settings of all factors for that run.
Factor values are normalized so that the cube points take values
between -1 and 1.
D=CCDESIGN(NFACTORS,'PNAME1',pvalue1,'PNAME2',pvalue2,...)
allows you to specify additional parameters and their values.
Valid parameters are the following:
Parameter Value
'center' The number of center points to include, or 'uniform'
to select the number of center points to give uniform
precision, or 'orthogonal' (the default) to give an
orthogonal design.
'fraction' Fraction of full factorial for cube portion expressed
as an exponent of 1/2: 0 = whole design, 1 = 1/2
fraction, 2 = 1/4 fraction, etc.
'type' Either 'inscribed', 'circumscribed', or 'faced'.
'blocksize' The maximum number of points allowed in a block.
[D,BLK]=CCDESIGN(...) requests a blocked design. The output
vector BLK is a vector of block numbers. Blocks are groups of
runs that are to be measured under similar conditions (for example,
on the same day). Blocked designs minimize the effect of between-
block differences on the parameter estimates.
See also BBDESIGN, ROWEXCH, CORDEXCH.
Reference page in Doc Center
doc ccdesign
In [17]:
dCCD_1=ccdesign(2,'center',1, 'type','faced')
dCCD_1 =
-1 -1
-1 1
1 -1
1 1
-1 0
1 0
0 -1
0 1
0 0
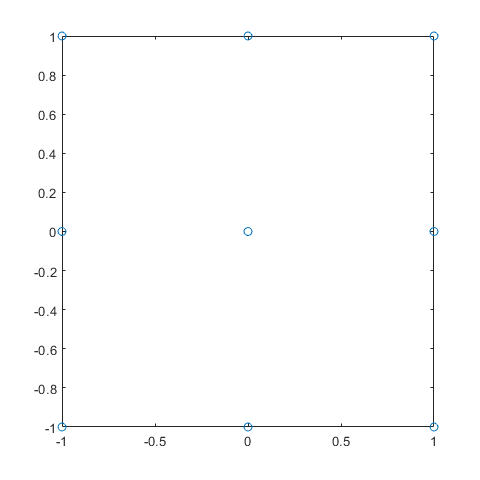
In [18]:
plot(dCCD_1(:,1),dCCD_1(:,2),'o')
In [19]:
dCCD_2=ccdesign(2,'center',1, 'type','circumscribed')
dCCD_2 =
-1.0000 -1.0000
-1.0000 1.0000
1.0000 -1.0000
1.0000 1.0000
-1.4142 0
1.4142 0
0 -1.4142
0 1.4142
0 0
In [20]:
dCCD_3=ccdesign(2,'center',1, 'type','inscribed')
dCCD_3 =
-0.7071 -0.7071
-0.7071 0.7071
0.7071 -0.7071
0.7071 0.7071
-1.0000 0
1.0000 0
0 -1.0000
0 1.0000
0 0
In [21]:
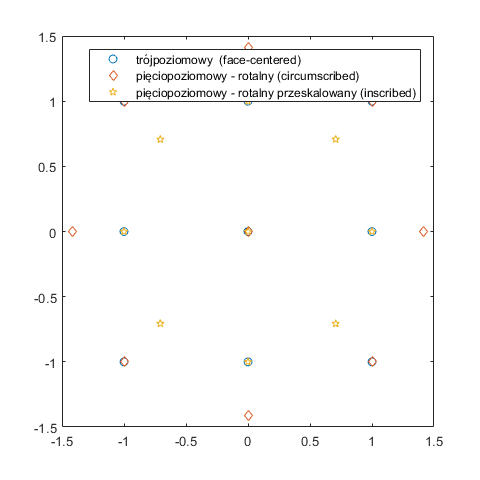
plot(dCCD_1(:,1),dCCD_1(:,2),'o',dCCD_2(:,1),dCCD_2(:,2),'d',dCCD_3(:,1),dCCD_3(:,2),'p')
legend('trójpoziomowy (face-centered)', 'pięciopoziomowy - rotalny (circumscribed)','pięciopoziomowy - rotalny przeskalowany (inscribed)')
Plany równomiernie wypełniające przestrzeń¶
In [22]:
%plot inline -w 600 -h 600
Plan losowy o rozkładzie prawdopodobieństwa jednostajnym¶
In [23]:
help rand
RAND Uniformly distributed pseudorandom numbers.
R = RAND(N) returns an N-by-N matrix containing pseudorandom values drawn
from the standard uniform distribution on the open interval(0,1). RAND(M,N)
or RAND([M,N]) returns an M-by-N matrix. RAND(M,N,P,...) or
RAND([M,N,P,...]) returns an M-by-N-by-P-by-... array. RAND returns a
scalar. RAND(SIZE(A)) returns an array the same size as A.
Note: The size inputs M, N, P, ... should be nonnegative integers.
Negative integers are treated as 0.
R = RAND(..., CLASSNAME) returns an array of uniform values of the
specified class. CLASSNAME can be 'double' or 'single'.
R = RAND(..., 'like', Y) returns an array of uniform values of the
same class as Y.
The sequence of numbers produced by RAND is determined by the settings of
the uniform random number generator that underlies RAND, RANDI, and RANDN.
Control that shared random number generator using RNG.
Examples:
Example 1: Generate values from the uniform distribution on the
interval (a, b).
r = a + (b-a).*rand(100,1);
Example 2: Use the RANDI function, instead of RAND, to generate
integer values from the uniform distribution on the set 1:100.
r = randi(100,1,5);
Example 3: Reset the random number generator used by RAND, RANDI, and
RANDN to its default startup settings, so that RAND produces the same
random numbers as if you restarted MATLAB.
rng('default')
rand(1,5)
Example 4: Save the settings for the random number generator used by
RAND, RANDI, and RANDN, generate 5 values from RAND, restore the
settings, and repeat those values.
s = rng
u1 = rand(1,5)
rng(s);
u2 = rand(1,5) % contains exactly the same values as u1
Example 5: Reinitialize the random number generator used by RAND,
RANDI, and RANDN with a seed based on the current time. RAND will
return different values each time you do this. NOTE: It is usually
not necessary to do this more than once per MATLAB session.
rng('shuffle');
rand(1,5)
See <a href="matlab:helpview([docroot '\techdoc\math\math.map'],'update_random_number_generator')">Replace Discouraged Syntaxes of rand and randn</a> to use RNG to replace
RAND with the 'seed', 'state', or 'twister' inputs.
See also RANDI, RANDN, RNG, RANDSTREAM, RANDSTREAM/RAND,
SPRAND, SPRANDN, RANDPERM.
Reference page in Doc Center
doc rand
Other functions named rand
codistributed.rand codistributor2dbc/rand gpuArray.rand
codistributor1d/rand distributed.rand RandStream/rand
In [24]:
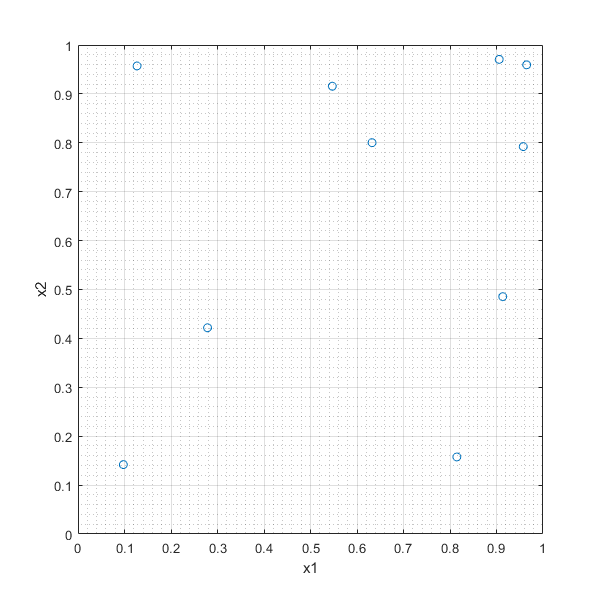
RANDd=rand(10,2)
plot(RANDd(:,1),RANDd(:,2),'o'),xlabel('x1'),ylabel('x2'),grid on, grid minor
xlim([0 1]),ylim([0 1])
RANDd =
0.8147 0.1576
0.9058 0.9706
0.1270 0.9572
0.9134 0.4854
0.6324 0.8003
0.0975 0.1419
0.2785 0.4218
0.5469 0.9157
0.9575 0.7922
0.9649 0.9595
In [25]:
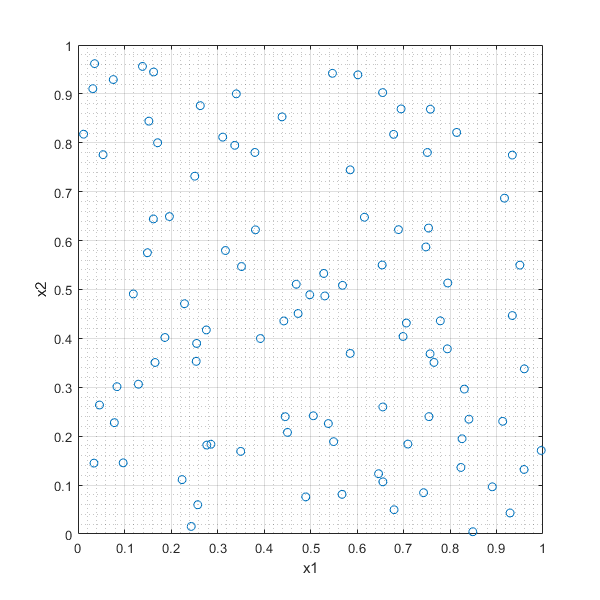
RANDd=rand(100,2);
plot(RANDd(:,1),RANDd(:,2),'o'),xlabel('x1'),ylabel('x2'),grid on, grid minor
In [26]:
%doc cov
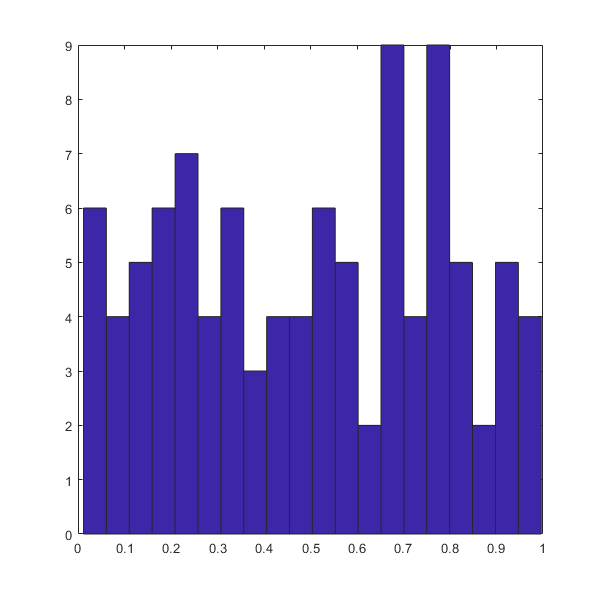
covM=cov(RANDd)
%doc hist
hist(RANDd(:,1),20)
covM =
0.0803 -0.0180
-0.0180 0.0796
Plan losowy o rozkładzie prawdopodobieństwa normalnym¶
In [27]:
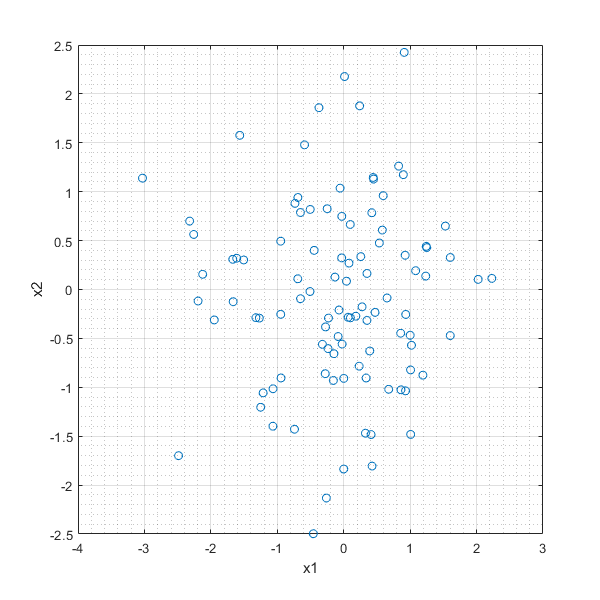
RANDNd=randn(100,2);
plot(RANDNd(:,1),RANDNd(:,2),'o'),xlabel('x1'),ylabel('x2'),grid on, grid minor
In [28]:
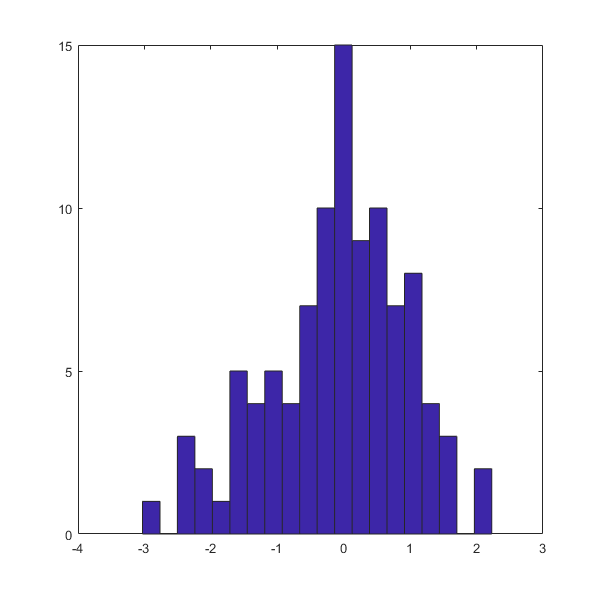
covM=cov(RANDNd)
hist(RANDNd(:,1),20)
covM =
1.0653 0.0035
0.0035 0.8834
Plan na podstawie wielowymiarowych sześcianów łacińskich (ang. LHS)¶
In [29]:
help lhsdesign
LHSDESIGN Generate a latin hypercube sample.
X=LHSDESIGN(N,P) generates a latin hypercube sample X containing N
values on each of P variables. For each column, the N values are
randomly distributed with one from each interval (0,1/N), (1/N,2/N),
..., (1-1/N,1), and they are randomly permuted.
X=LHSDESIGN(...,'PARAM1',val1,'PARAM2',val2,...) specifies parameter
name/value pairs to control the sample generation. Valid parameters
are the following:
Parameter Value
'smooth' 'on' (the default) to produce points as above, or
'off' to produces points at the midpoints of
the above intervals: .5/N, 1.5/N, ..., 1-.5/N.
'iterations' The maximum number of iterations to perform in an
attempt to improve the design (default=5)
'criterion' The criterion to use to measure design improvement,
chosen from 'maximin' (the default) to maximize the
minimum distance between points, 'correlation' to
reduce correlation, or 'none' to do no iteration.
Latin hypercube designs are useful when you need a sample that is
random but that is guaranteed to be relatively uniformly distributed
over each dimension.
Example: The following commands show that the output from lhsdesign
looks uniformly distributed in two dimensions, but too
uniform (non-random) in each single dimension. Repeat the
same commands with x=rand(100,2) to see the difference.
x = lhsdesign(100,2);
subplot(2,2,1); plot(x(:,1), x(:,2), 'o');
subplot(2,2,2); hist(x(:,2));
subplot(2,2,3); hist(x(:,1));
See also LHSNORM, UNIFRND.
Reference page in Doc Center
doc lhsdesign
In [30]:
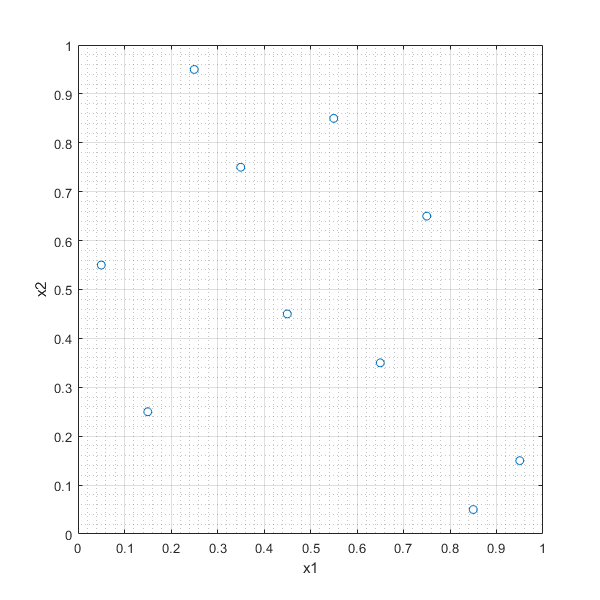
LHSd=lhsdesign(10,2,'smooth','off','criterion','none','iterations',1)
plot(LHSd(:,1),LHSd(:,2),'o'),xlabel('x1'),ylabel('x2'),grid on, grid minor
LHSd =
0.0500 0.5500
0.2500 0.9500
0.1500 0.2500
0.3500 0.7500
0.4500 0.4500
0.7500 0.6500
0.5500 0.8500
0.8500 0.0500
0.6500 0.3500
0.9500 0.1500
In [31]:
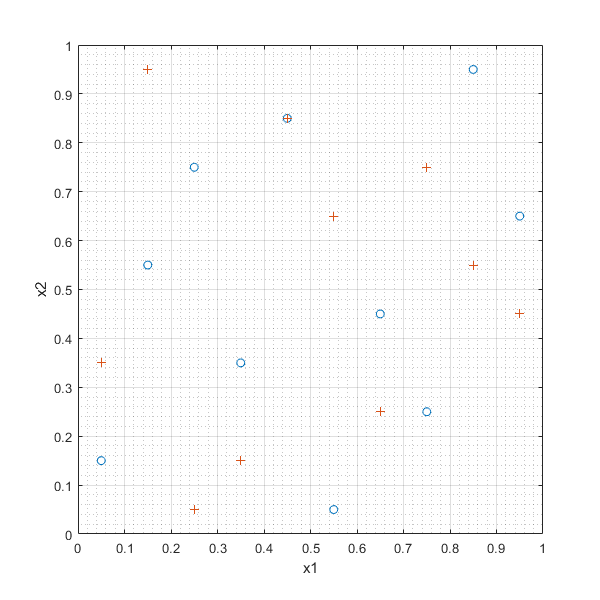
LHSd_1=lhsdesign(10,2,'smooth','off','criterion','maximin','iterations',100)
LHSd_2=lhsdesign(10,2,'smooth','off','criterion','correlation','iterations',100)
plot(LHSd_1(:,1),LHSd_1(:,2),'o',LHSd_2(:,1),LHSd_2(:,2),'+'),xlabel('x1'),ylabel('x2'),grid on, grid minor
LHSd_1 =
0.4500 0.8500
0.8500 0.9500
0.6500 0.4500
0.5500 0.0500
0.0500 0.1500
0.1500 0.5500
0.2500 0.7500
0.7500 0.2500
0.3500 0.3500
0.9500 0.6500
LHSd_2 =
0.0500 0.3500
0.7500 0.7500
0.6500 0.2500
0.1500 0.9500
0.5500 0.6500
0.3500 0.1500
0.8500 0.5500
0.4500 0.8500
0.9500 0.4500
0.2500 0.0500
In [32]:
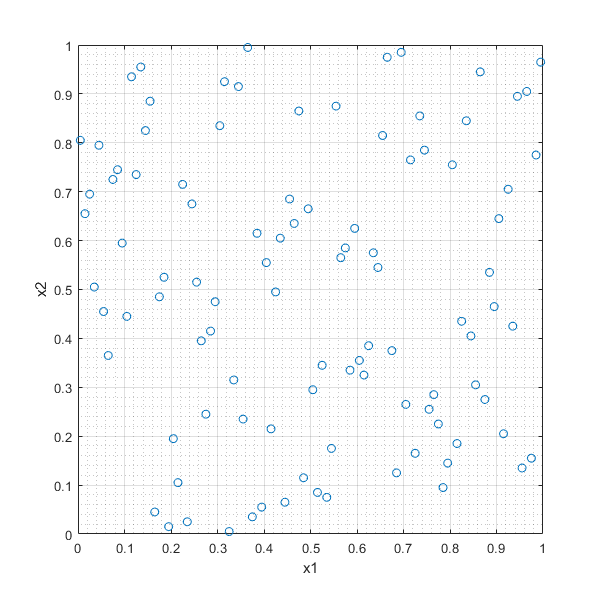
LHSd=lhsdesign(100,2,'smooth','off','criterion','maximin','iterations',100);
plot(LHSd(:,1),LHSd(:,2),'o'),xlabel('x1'),ylabel('x2'),grid on, grid minor
In [33]:
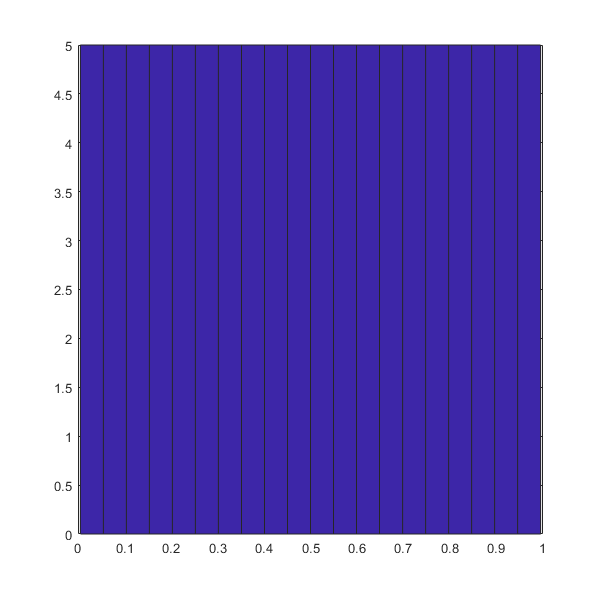
hist(LHSd(:,1),20)
Plan LHS o rozkładzie prawdopodobieństwa normalnym¶
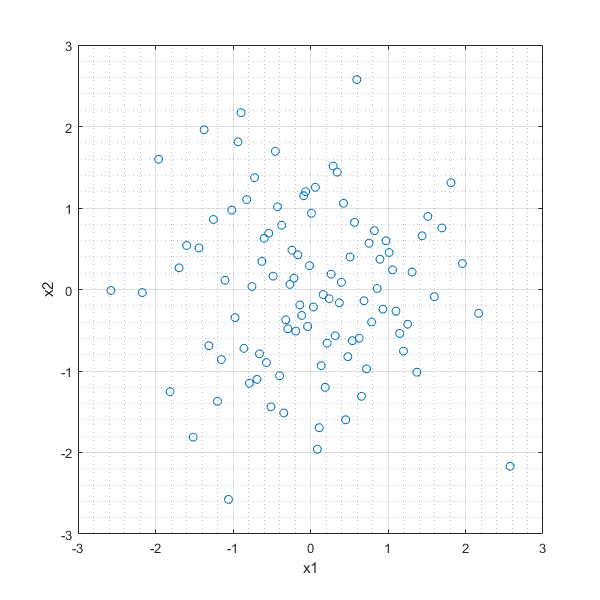
In [34]:
mu=[0 0]; %wartość średnia
sigma=[1 0
0 1]; %macierz kowariancji
n=100; %liczba punktów
flag='off'; %wygładzanie
LHSNd = lhsnorm(mu,sigma,n,flag);
plot(LHSNd(:,1),LHSNd(:,2),'o'),xlabel('x1'),ylabel('x2'),grid on, grid minor
In [35]:
hist(LHSNd(:,1),20)