format compact

Wrażliwość lokalna (analitycznie)

Przemieszczenia belki jednostronnie utwierdzonej

Dana jest belka o długości \(L\) z materiału o module Younga \(E\) posiadająca przekrój prostokątny o momencie bezwładności \(I\) (wyznaczonym na podstawie jego szerokości \(w\) i wysokości \(h\)). Równanie różniczkowe opisujące ugięcie belki utwierdzonej na jedmym końcu (dla \(x=L\)) z obciążeniem ciągłym \(Q\) ma postać

\[\mathrm{EI}\,\frac{\partial ^4}{\partial x^4} y\left(x\right)=Q\]

clear all
syms y(x) E I Q L w h

D4y=diff(y,x,4);
ode = E*I*D4y == Q

ySol(x) = dsolve(ode)

ode(x) =
E*I*diff(y(x), x, x, x, x) == Q
ySol(x) =
(Q*x^4)/(24*E*I) + (C1*x^3)/6 + (C2*x^2)/2 + C3*x + C4

Stałe \(C_1\) do \(C_4\) wyznacza się poprzez uwzględnienie warunków brzegowych

Dy  = diff(y,x,1);
D2y = diff(y,x,2);
D3y = diff(y,x,3);
cond=[D2y(0)==0, D3y(0)==0, y(L)==0, Dy(L)==0];
ySolC(x) = dsolve(ode, cond)

ySolC(x) =
(Q*L^4)/(8*E*I) - (Q*L^3*x)/(6*E*I) + (Q*x^4)/(24*E*I)

Maksymalne ugięcie jest na swobodnym końcu belki ( \(x=0\))

y_max=ySolC(0)
y_max=subs(y_max, I, (w*h^3)/12)

y_max =
(L^4*Q)/(8*E*I)
y_max =
(3*L^4*Q)/(2*E*h^3*w)

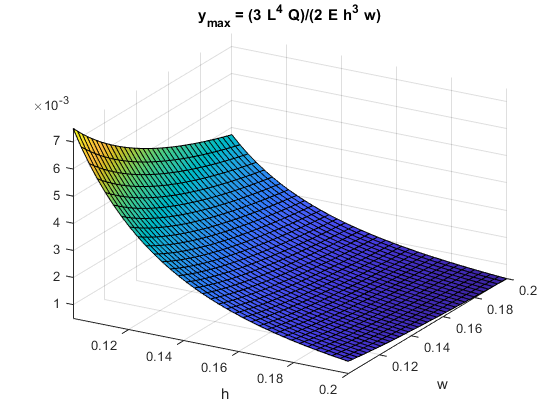
Zakładając, że \(L=1\) m, \(E=2 \cdot 10^{11}\) Pa, \(Q = 10^{5}\) N/m, oraz że \(w\) i \(h\) zawierają się w przedziale \([0.1, 0.2]\) m

y_1=subs(y_max, [L E Q], [1 2e11 1e5])

y_1 =
3/(4000000*h^3*w)

fsurf(y_1,[.1 .2])   %dla Matlab 2014a 'ezsurf()'
xlabel('h'), ylabel('w')
title(['y_{max} = ' texlabel(y_max)])
view(30,30)

Naprężenia w belce jednostronnie utwierdzonej

Naprężenia maksymalne w belce jednostronnie utwierdzonej o długości \(L\) i przekroju prostokątnym o momencie bezwładności \(I\) (szerokości \(w\) i wysokości \(h\)) z obciążeniem ciągłym \(Q\) na całej długości wynoszą

\[M_{max} = (QL)(L/2)\]

\[\sigma_{max}(w,h)=\frac{M_{max}\frac{h}{2}}{I} ,~~ I = \frac{wh^3}{12}\]

syms w h I Q L

M_max = (Q*L)*(L/2)
sigma=(M_max*(h/2))/I
sigma=subs(sigma,I,(w*h^3)/12)

M_max =
(L^2*Q)/2
sigma =
(L^2*Q*h)/(4*I)
sigma =
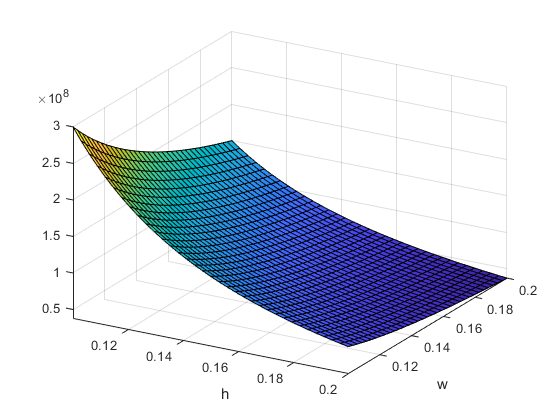
(3*L^2*Q)/(h^2*w)

y_2=subs(sigma,[Q L],[1e5 1]);
fsurf(y_2,[0.1 0.2 0.1 0.2])    %dla Matlab 2014a 'ezsurf()'
xlabel('h'), ylabel('w')
view(30,30)

Wrażliwość kształtu

Przemieszczenia

Przemieszczenia maksymalne w belce jednostronnie utwierdzonej, z materiału o module Younga \(E\) i przekroju prostokątnym o szerokości \(w\) i wysokości \(h\), z obciążeniem ciągłym \(Q\) na całej długości \(L\), wynoszą

\[y_{max}=\frac{3\,L^3\,Q}{2 E\,h^3\,w}\]

syms w h Q L E                    %kontynuując poprzedni przykład zbędne
y_max = (3*L^4*Q)/(2*E*h^3*w)     %kontynuując poprzedni przykład zbędne

y_max =
(3*L^4*Q)/(2*E*h^3*w)

S_wy=diff(y_max,w), S_hy=diff(y_max,h)

S_wy =
-(3*L^4*Q)/(2*E*h^3*w^2)
S_hy =
-(9*L^4*Q)/(2*E*h^4*w)

Wrażliwość definiuje się jako pochodną \(S_{wy} = \frac{\partial y_{max}}{\partial w}\) , \(S_{hy} = \frac{\partial y_{max}}{\partial h}\)

S_wy=diff(y_max,w), S_hy=diff(y_max,h)

S_wy =
-(3*L^4*Q)/(2*E*h^3*w^2)
S_hy =
-(9*L^4*Q)/(2*E*h^4*w)

Zakładając \(w=h=0.1\) wrażliwość lokalna wyniesie

S_wy=subs(S_wy, [w h], [.1 .1]), S_hy=subs(S_hy, [w h], [.1 .1])

S_wy =
-(150000*L^4*Q)/E
S_hy =
-(450000*L^4*Q)/E

Naprężenia

Naprężenia maksymalne w belce jednostronnie utwierdzonej o długości \(L\) i przekroju prostokątnym o szerokości \(w\) i wysokości \(h\) z obciążeniem ciągłym \(Q\) na całej długości wynoszą

\[\sigma_{max}(w,h)=\frac{3\,L^2\,Q}{h^2\,w}\]

syms w h Q L

sigma_max = (3*L^2*Q)/(h^2*w)

sigma_max =
(3*L^2*Q)/(h^2*w)

Wrażliwość definiuje się jako pochodną \(S_{ws} = \frac{\partial \sigma_{max}}{\partial w}\) , \(S_{hs} = \frac{\partial \sigma_{max}}{\partial h}\)

S_ws=diff(sigma_max,w), S_hs=diff(sigma_max,h)

S_ws =
-(3*L^2*Q)/(h^2*w^2)
S_hs =
-(6*L^2*Q)/(h^3*w)

Zakładając \(w=h=0.1\) wrażliwość lokalna wyniesie

S_ws=subs(S_ws, [w h], [.1 .1]), S_hs=subs(S_hs, [w h], [.1 .1])

S_ws =
-30000*L^2*Q
S_hs =
-60000*L^2*Q