Table of Contents
Laboratorium 3: Regresja liniowa
Zbiory danych
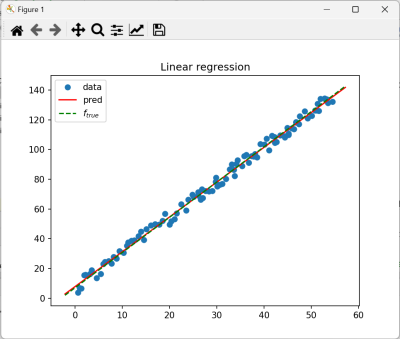
- xy-001 $f_{true}=2.37x+7$
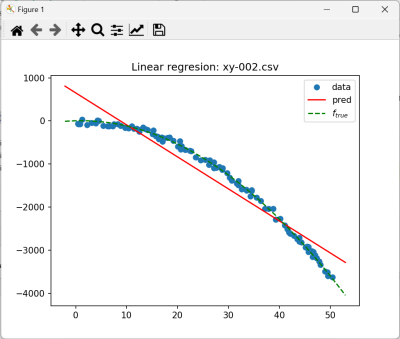
- xy-002 $f_{true}=-1.5x^2+3x+4$
- xy-003 $f_{true}=-1.5x^2+3x+4$
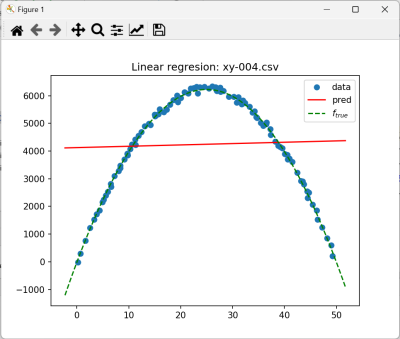
- xy-004 $f_{true}=-10x^2+500x-25$
- xy-005 $f_{true}=(x+4)(x+1)(x-3)$
- xy-006 box
- xy-007 circle
- xy-008 fat-ellipse
- xy-009 ellipse
- xy-010 ellipse-outliers
1. Przetwarzamy zbiór xy-001
1.1. Ładowanie i przetwarzanie wstępne
1. Załaduj zbiór danych i wyświetl zawartość
2. Algorytm regresji działa na danych numerycznych. Kolumny X i Y są danymi numerycznymi, ale wejściem dla algorytmu jest wektor cech. Dlatego X musi być przekonwertowane do postaci wektora.
Uzyj klasy VectorAssembler, a w szczególności metod:
setInputCols()- jedyną kolumną do przekonwertowania jestXsetOutputCol(“features”)- po konwersji kolumna z wektorami danych ma się nazywaćfeaturestransform()do przekonwertowania danych
Oczekiwany wynik:
+--------+---------+----------+ | X| Y| features| +--------+---------+----------+ |0.581807| 3.930072|[0.581807]| |0.969903| 6.831824|[0.969903]| | 1.03564| 6.630985| [1.03564]| |1.284787| 6.558356|[1.284787]| |1.949874|15.588728|[1.949874]| +--------+---------+----------+ only showing top 5 rows root |-- X: double (nullable = true) |-- Y: double (nullable = true) |-- features: vector (nullable = true)
1.2 Regresja
Typowy przebieg procesu uczenia to
- Definiowanie algorytmu i jego parametrów - klasa
LinearRgression - Budowa modelu - klasa
LinearRegressionModel - Ocena modelu (w tym przypadku tylko dla zbioru uczącego na podstawie danych zebranych w obiekcie klasy
LinearRegressionTrainingSummary)
1. Dodaj poniższy kod
LinearRegression lr = new LinearRegression() .setMaxIter(10) .setRegParam(0.3) .setElasticNetParam(0.8) .setFeaturesCol("features") .setLabelCol("Y"); // Fit the model. LinearRegressionModel lrModel = lr.fit(df_trans);
2. Wydrukuj współczynniki regresji za pomocą metod + lrModel.coefficients() oraz lrModel.intercept()
3. Wyświetl informacje o przebiegu uczenia i metryki
LinearRegressionTrainingSummary trainingSummary = lrModel.summary(); System.out.println("numIterations: " + trainingSummary.totalIterations()); System.out.println("objectiveHistory: " + Vectors.dense(trainingSummary.objectiveHistory())); trainingSummary.residuals().show(100); System.out.println("MSE: " + trainingSummary.meanSquaredError()); System.out.println("RMSE: " + trainingSummary.rootMeanSquaredError()); System.out.println("MAE: " + trainingSummary.meanAbsoluteError()); System.out.println("r2: " + trainingSummary.r2());
4. Jakie metryki są wyświetlane. Co to są residuals
5 Wyświetl historię uczenia trainingSummary.objectiveHistory() za pomocą poniższej funkcji:
static void plotObjectiveHistory(List<Double> lossHistory){ var x = IntStream.range(0,lossHistory.size()).mapToDouble(d->d).boxed().toList(); Plot plt = Plot.create(); plt.plot().add(x, lossHistory).label("loss"); plt.xlabel("Iteration"); plt.ylabel("Loss"); plt.title("Loss history"); plt.legend(); try { plt.show(); } catch (IOException e) { throw new RuntimeException(e); } catch (PythonExecutionException e) { throw new RuntimeException(e); } }
1.3 Wykres funkcji i danych
Napisz funkcję służącą do rysowania wykresów:
- danych
- przebiegu funkcji regresji
- opcjonalnie: $f_{true}$ - prawdziwej funkcji z której został wygenerowany zbiór danych
/** * * @param x - współrzedne x danych * @param y - współrzedne y danych * @param lrModel - model regresji * @param title - tytuł do wyswietlenia (może być null) * @param f_true - funkcja f_true (może być null) */ static void plot(List<Double> x, List<Double> y, LinearRegressionModel lrModel, String title, Function<Double,Double> f_true){
1. Rysowanie danych x,y jest proste
Plot plt = Plot.create(); plt.plot().add(x, y,"o").label("data");
2. Oblicz zakresy zmienności x – zmienne xmin i xmax i wygeneruj listę punktów
var xdelta = 0.05*(xmax-xmin); var fx = NumpyUtils.linspace(xmin-xdelta,xmax+xdelta,100);
3. Dla wszystkich wartości w fx:
- przekształć je do postaci jednoelemntowego wektora typu
DenseVectorhttps://spark.apache.org/docs/latest/api/java/org/apache/spark/ml/linalg/DenseVector.html - wywołaj
lrModel.predict()z wektorem jako argumentem - zgromadź wartości na liście
fy - najkrócej - strumieniem i map
Wyświetl:
plt.plot().add(fx, fy).color("r").label("pred");
Jeżeli f_true!=null oblicz jej wartość dla każdego elementu fx: f_true.apply(_x) i zgromadź wynik na liście. Następnie wyświetl:
plt.plot().add(fx, fy_true).color("g").linestyle("--").label("$f_{true}$");
1.4 Potencjalny wpływ parametrów algorytmu
Zaimplementowany w Apache Spark algorytm liniowej regresji może:
- Ustawić wagę składników regularyzacji w funkcji straty, lub je pominąć co odpowiada setRegParam(0.0)
- Mieszać składniki regularyzacji L1 i L2 ustwiajac proporcje za pomocą
setElasticNetParam(alpha). Cytując dokumentację: Param for the ElasticNet mixing parameter, in range [0, 1]. For alpha = 0, the penalty is an L2 penalty. For alpha = 1, it is an L1 penalty.
1. Ile iteracji zaobserwowano, jeżeli ustawiono setRegParam(0.0)
2. Przetestuj dla wartości parametru regularyzacji 10,20,50,100
- Jak wyglądają wykresy (zamieść rysunki)
- Jak zmieniają się miary, np. współczynnik determinacji r2
2. Przetwarzamy kolejne zbiory
Dla kolejnych zbiorów danych:
- Wyświetl wykresy
- Wyznacz metryki i zbierz ich wartości w tabelce
3. Porównanie xy-002 i xy-004
3.1 Wyniki regresji dla xy-002
Użyj następującego kodu w języku Python, aby wyświetlić informacje statystyczne dotyczące wyznaczonych współczynników. W tym przypadku stosowana jest metoda OLS (ang. ordinary least squares, czyli czysta regresja bez regularyzacji $𝑤=[X^TX]^{-1}X^Ty$ ). Metoda wymaga dodania kolumny z jedynkami na początku tablicy z danymi.
import numpy as np import statsmodels.api as sm x,y = np.loadtxt('xy-002.csv',delimiter=',',unpack=True,skiprows=1) X_plus_one = np.stack( (np.ones(x.size),x), axis=-1) X_plus_one ols = sm.OLS(y, X_plus_one) ols_result = ols.fit() print(ols_result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.933
Model: OLS Adj. R-squared: 0.933
Method: Least Squares F-statistic: 1370.
Date: Sat, 09 Mar 2024 Prob (F-statistic): 2.10e-59
Time: 18:20:11 Log-Likelihood: -711.10
No. Observations: 100 AIC: 1426.
Df Residuals: 98 BIC: 1431.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 652.8037 60.627 10.768 0.000 532.491 773.116
x1 -74.3271 2.008 -37.012 0.000 -78.312 -70.342
==============================================================================
Omnibus: 11.135 Durbin-Watson: 0.062
Prob(Omnibus): 0.004 Jarque-Bera (JB): 7.706
Skew: -0.547 Prob(JB): 0.0212
Kurtosis: 2.191 Cond. No. 61.2
==============================================================================
- Jaką wartość ma współczynnik determinacji?
- Jaki jest błąd standardowy wyznaczonych współczynników?
- W jakim zakresie mieszczą się z 95% wiarygodnością?