Laboratorium 4: Cechy wielomianowe

Będziemy przetwarzali następujące pliki:

• xy-002 $f_{true}=-1.5x^2+3x+4$
• xy-003 $f_{true}=-1.5x^2+3x+4$
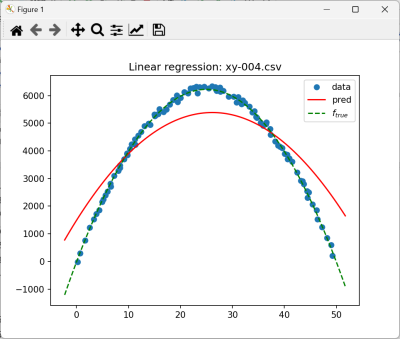
• xy-004 $f_{true}=-10x^2+500x-25$
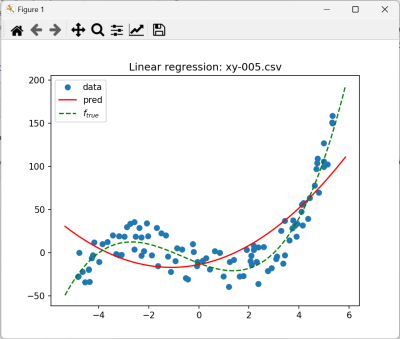
• xy-005 $f_{true}=(x+4)(x+1)(x-3)$

Wykorzystamy kod z poprzedniego laboratorium (Regresja Liniowa)

Umieść kod w klasie LinearRegressionPolynomialFeaturesOrderTwo

Ponieważ przetwarzane są kolejne zbiory, najwygodniej będzie umieścić kod w funkcji postaci
static void processDataset(SparkSession spark,String filename,Function<Double,Double> f_true)

1. Dodaj do zbioru danych kolumnę X2 zawierającą po prostu wynik wyrażenia “X*X”

Czyli, np. dla xy-002.csv po załadowaniu i przetworzeniu danych wynikiem będzie:

+--------+----------+------------------+
|       X|         Y|                X2|
+--------+----------+------------------+
|0.411194|-59.938274|    0.169080505636|
|0.549662|-72.006761|    0.302128314244|
|0.860093|-68.979336|    0.739759968649|
| 1.27504|  32.07157|1.6257270015999998|
|2.202931|-91.531894|    4.852904990761|
+--------+----------+------------------+
only showing top 5 rows

root
 |-- X: double (nullable = true)
 |-- Y: double (nullable = true)
 |-- X2: double (nullable = true)

2. Zmień konfigurację VectorAssembler tak, aby budował wektory na podstawie kolumn [“X”, “X2”]

3. Zbuduj model regresji

4. Wyświetl wyniki. Przy wyświetlaniu aproksymowanej funkcji wywoływana jest funkcja lrModel.predict(). Jako argument musisz dostarczyć wektor zawierający zarówno wartość wejściową, jak i jej kwadrat. Możesz to zrealizować dodają parametr order do funkcji plot (przyda się przy regresji 3-stopnia) lub po prostu dodając element.

5. Przetwórz wszystkie pliki i wyświetl ich wykresy oraz w każdym przypadku podaj równanie regresji

Niewątpliwie ciekawym wykresem jest dopasowanie wielomianu 2-stopnia do danych wygenerowanych z wielomianu 3 stopnia

ale bardziej zastanawiający jest przypadek xy-004.csv

6. Popraw dopasowanie (jest to możliwe)

Przeanalizuj parametry algorytmu. Na przykład:

        LinearRegression lr = new LinearRegression()
                .setMaxIter(10)
                .setRegParam(0.3)
                .setElasticNetParam(0.8)
                .setFeaturesCol("features")
                .setLabelCol("Y");

Które z nich można zmienić? Sprawdź, co się stanie, gdy

• usuniemy regularyzację
• zwiększymy liczbę iteracji
• Porównaj metryki, zamieśc wykresy

Uwagi:

• usuwanie regularyzacji na ogół (dla niesyntetycznych zbiorów danych) psuje zdolność generalizacji
• zwiększenie liczby iteracji dla dużych zbiorów danych proporcjonalnie zwiększa czas uczenia

Umieść kod w klasie LinearRegressionPolynomialFeaturesOrderThree

1. Podobnie, jak w poprzednim przypadku dodaj kolumnę X3 z wartościami kolumny X podniesionymi do 3 potęgi

2. Zmodyfikuj odpowiednio VectorAssembler

3. Przeprowadź regresję (dla wszystkich zbiorów danych)

4. Zamieść wykres xy-005.csv

5. Porównaj w tabelce wartości miary r2 i MSE dla regresji 2 i 3 stopnia (dla wszystkich zbiorów danych)

• Sprawdź, czy w przypadku regresji 3-stopnia dla danych wygenerowanych z funkcji kwadratowej współczynniki przy $x^3$ były zerowe?
• Z reguły niewielkie zwiększenie współczynnika regularyzacji i liczby iteracji poprawia dopasowanie dla krzywych 2 stopnia

Kod umieść w klasie LinearRegressionPolynomialFeaturesPipeline

Ponieważ przetwarzane są kolejne zbiory, najwygodniej będzie umieścić kod w funkcji postaci
static void processDataset(SparkSession spark,String filename,int degree,Function<Double,Double> f_true)

Dodawanie manualne cech jako kolumn zbioru danych jest zbyt żmudne - zachodzi konieczność nazywania tych kolumn, później modyfikacji kodu w kilku miejscach. Raczej buduje się ciąg przetwarzania: Pipeline, którego elementami są wstępne przetwarzanie danych i budowa modelu estymatora.

Rozszerzenie cech o cechy wielomianowe jest dokonywane za pomocą odpowiedniej funkcji transformującej dane tablicowe : PolynomialExpansion.

Kolejne etapy przetwarzania to:

• zastosowanie VectorAssembler
• PolynomialExpansion
• LinearRegression

Zamiast wykonywać je natychmiast utwórz i skonfiguruj odpowiednie obiekty

 VectorAssembler vectorAssembler=new VectorAssembler()
                .setInputCols(new String[]{"X"})
                .setOutputCol("features");
 
//        Dataset<Row> df_trans = vectorAssembler.transform(df);
 
        PolynomialExpansion polyExpansion = new PolynomialExpansion()
                .setInputCol("features")
                .setOutputCol("polyFeatures")
                .setDegree(degree);
 
//        df_trans = polyExpansion.transform(df_trans);
 
        LinearRegression lr = new LinearRegression()
        ...

a następnie zdefinuj ciąg przetwarzania Pipeline i wywołaj jego metodę fit()

Pipeline pipeline = new Pipeline()
                        .setStages(new PipelineStage[] {vectorAssembler, polyExpansion, lr});
PipelineModel model = pipeline.fit(df);

Aby uzyskać dostęp do konkretnego elementu ciagu - nalezy po prostu zrzutować wybrany element

LinearRegressionModel lrModel = (LinearRegressionModel)model.stages()[2];

Zmodyfikujemy sygnaturę funkcji.

     *
     * @param x - współrzedne x danych
     * @param y - współrzedne y danych
     * @param pipelineModel - model pipeline
     * @param spark - sesja Spark
     * @param title - tytuł do wyswietlenia (może być null)
     * @param f_true - funkcja f_true (może być null)
     */
    static void plot(List<Double>x, List<Double> y, PipelineModel pipelineModel, SparkSession spark, String title, Function<Double,Double> f_true)

W odróżnieniu od funkcji używanej dotychczas - przekazujemy do niej pipelineModel. Wykorzystamy go, aby wyświetlić przebieg funkcji wyznaczonej w wyniku regresji.

1. Załóżmy, że mamy punkty, dla których mamy wyznaczyć wartości funkcji zgromadzone na liście fx

var xdelta = 0.05*(xmax-xmin);
var fx = NumpyUtils.linspace(xmin-xdelta,xmax+xdelta,100);

Aby przetworzyć je za pomocą pipeline musimy zamienić je na obiekt typu Dataset<Row> zawierający kolumnę o nazwie X z odpowiednimi wartościami.

2. Zamiana wartości double na Row

Przeiteruj przez elementy fx i dla każdego z nich utwórz obiekt Row, np. wołając Row r = RowFactory.create(d); lub umieść takie odwzorowanie w odpowiedniej funkcji strumienia. Zbierz wynik w List<Row> rows

3. Zdefiniuj schemat i utwórz zbiór danych:

StructType schema = new StructType().add("X", "double");
 
Dataset<Row> df_test =  spark.createDataFrame(rows,schema);
df_test.show(5);
df_test.printSchema();

Wynik:

+--------------------+
|                   X|
+--------------------+
|          -2.0917333|
| -1.5355272333333332|
| -0.9793211666666666|
|-0.42311509999999974|
| 0.13309096666666687|
+--------------------+
only showing top 5 rows

3. Wywołaj funkcję transform() obiektu pipeline

Dataset<Row> df_pred = pipelineModel.transform(df_test);
df_pred.show(5);
df_pred.printSchema();

W wyniku jej wykonania do zbioru zostaną dodane kolejno kolumny features, polyfeatures i prediction zgodnie z kolejnymi etapami przetwarzania

+--------------------+--------------------+--------------------+-------------------+
|                   X|            features|        polyFeatures|         prediction|
+--------------------+--------------------+--------------------+-------------------+
|          -2.0917333|        [-2.0917333]|[-2.0917333,4.375...| -33.40167605867543|
| -1.5355272333333332|[-1.5355272333333...|[-1.5355272333333...|-29.392038747489657|
| -0.9793211666666666|[-0.9793211666666...|[-0.9793211666666...| -26.24979833578732|
|-0.42311509999999974|[-0.4231150999999...|[-0.4231150999999...|-23.976336940609087|
| 0.13309096666666687|[0.13309096666666...|[0.13309096666666...| -22.57303667899562|
+--------------------+--------------------+--------------------+-------------------+
only showing top 5 rows

root
 |-- X: double (nullable = true)
 |-- features: vector (nullable = true)
 |-- polyFeatures: vector (nullable = true)
 |-- prediction: double (nullable = false)

4. Należy oczywiście wyświetlić zawartość kolumny prediction

1. Po załadowaniu zbioru do podziel go korzystając z funkcji limit i offset:

        long rowsCount = df.count();
        int trainCount = (int)(rowsCount*.7);
        var df_train = df.select("*").limit(trainCount);
        var df_test = df.select("*").offset(trainCount);
        System.out.println(df_train.count());
        System.out.println(df_test.count());

2. Zamień wywołania w kodzie tak, aby przetwarzany i wyświetlany był zbiór df_train

3. Dodaj wyświeltanie df_test:

        x = df_test.select("X").as(Encoders.DOUBLE()).collectAsList();
        y = df_test.select("Y").as(Encoders.DOUBLE()).collectAsList();
        plot(x,y,model,spark,String.format("Linear regression: %s (test data)",filename),f_true);

4. Dodaj kod odpowiedzialny za obliczanie metryk na zbiorze testowym

• wpierw przetrannsformuj go
• następnie oblicz metryki korzystając z kolumn Y i prediction

        var df_test_prediction = model.transform(df_test);
        RegressionEvaluator evaluator = new RegressionEvaluator()
                .setLabelCol("Y")
                .setPredictionCol("prediction")
                .setMetricName("rmse"); // or any other evaluation metric
        double rmse = evaluator.evaluate(df_test_prediction);
        evaluator.setMetricName("r2");
        double r2 = evaluator.evaluate(df_test_prediction);

5. Wydrukuj wartości metryk i obejrzyj wykresy

Podziały przetestuj na plikach

• xy-003.csv dla cech wielomianowych 3 stopnia.
• xy-005.csv dla cech wielomianowych 2 stopnia

Zapisz rysunki i metryki.

Zamień sposób podziału na losowy (np. zakomentuj poprzedni kod lub utwórz kopię klasy).

var dfs = df.randomSplit(new double[]{0.7,0.3});
var df_train = dfs[0];
var df_test = dfs[1];

1. Przetestuj takie same konfiguracje zbiorów danych i stopni wielomianu

Podział jest losowy. Może się zdarzyć, że w danym losowaniu osiągniemy nie najlepszy podział Można oczywiście ustawić seed i otrzymać powtarzalne wyniki (np. seed =3 wydaje się całkiem dobry).

2. Wróć do poprzedniego rozwiązania Stały podział może być całkiem dobry, jeżeli wcześniej dane zostały losowo pomieszane. Jest to częste podejście przy publikacji zbiorów testowych.

Dodaj przed podziałem następujący kod i porównaj wyniki:

df = df.orderBy(org.apache.spark.sql.functions.rand(3));

3. Zbierz w tabelce metryki dla wszystkich sposobów ustalania podziału