Table of Contents
Laboratorium 6: Regresja - przewidywanie cen sprzedaży domów
Celem zadania jest przewidywanie cen sprzedaży domów.
- Zbiór danych dotyczących sprzedaży domów dostępny na Kaggle.
- Jego lokalna kopia może zostać pobrana z kc_house_data.csv.zip lub z kc_house_data.csv.gz (bezpośrednio obsługiwana przez Spark)
Wykorzystamy środowisko PySpark (obraz dockera spark-jupyter z zajęć 5) ale bez klastra. Spark będzie uruchamiany w konfiguracji standalone.
1. Utworzenie sesji Spark i załadowanie danych
1. Uruchom obraz spark-jupyter
docker run -it --rm -v ".:/opt/spark/work-dir" -p 4040:4040 -p 8888:8888 -p 443:443 --network spark-network spark-jupyter /bin/bash
Dodano mapowanie portu 443:443, aby bezpośrednio uzyskać dostęp do zbioru danych
2. W konsoli kontenera wydaj komendę startującą serwer notatników jupyter-lab
sudo --preserve-env jupyter-lab --ip=0.0.0.0 --allow-root --IdentityProvider.token='pyspark'
Otwórz http://localhost:8888/lab?token=pyspark…
3. Edytuj kod w notatniku…
import pyspark from pyspark.sql import SparkSession from pyspark.sql.functions import * spark = SparkSession.builder.appName("KcHouseData").master("local[*]").getOrCreate()
Zamiast “local[*]” możesz uruchomić wcześniej klaster, i przeprowadzić oblicznia na klastrze. Konieczne jednak będzie modyfikacja sposobu udostępniania pliku węzłom obliczeniowym (jak na poprzednim laboratorium).
4. Załaduj i wyświetl zbiór danych
from pyspark import SparkFiles url = "https://dysk.agh.edu.pl/s/nWNWeirnCJDQycp/download/kc_house_data.csv.gz" spark.sparkContext.addFile(url) df = spark.read.csv(SparkFiles.get("kc_house_data.csv.gz"), header=True, inferSchema=True) df.show(5)
Dodanie pliku do kontekstu Sparka w środowisku rozproszonym pozwala na automatyczne udostępnienie go węzłom obliczeniowym. W przypadku klastra na Dokerze problemem jest zapewnienie dostępu do tego samego portu przez serwisy.
5. W środowisku PySpark możliwa jets konwersja zbioru danych do Pandas Dataframe
pdf = df.toPandas() print(pdf.info()) pdf.head()
2. Przetwarzanie wstępne
1. Kolumna date jest tekstem. Zamień ją na typ timestamp wywołując funkcję to_timestamp(“date”, “yyyyMMdd'T'HHmmss”). Wyświetl zawartość zbioru danych
2. Zamień kolumnę date już typu timestamp na liczbę za pomocą funkcji unix_timestamp() nowa kolumna może nazywać sięunixdate. Usuń kolumnę date - będzimey dalej przetwarzali atrybuty numeryczne.
3. Usuń kolumnę id
3. Regresja
Zakładamy, że po konwersjach zbiór danych identyfikowany jest przez zmienną df2.
from pyspark.ml.regression import LinearRegression from pyspark.ml.feature import VectorAssembler
1. Utwórz obiekt VectorAssembler ustawiając jako kolumny wejściowe kolumny df2 bez price. Atrybut df2.columns umożliwia dostęp do kolumn zbioru danych. Kolumną wyjściową ma być zwyczajoweo features.
2. Zdefiniuj parametry algorytmu i wywołaj algorytm uczenia
lr = LinearRegression()\ .setMaxIter(100)\ .setRegParam(3.0)\ .setElasticNetParam(0.5)\ .setFeaturesCol("features")\ .setLabelCol("price") model = lr.fit(....)
3. Wyświetl informacje o procesie uczenia
print(f'RMSE: {model.summary.rootMeanSquaredError}') print(f'r2: {model.summary.r2}') print(f'iterations: {model.summary.totalIterations}')
3.1 Train test split
from pyspark.ml.regression import LinearRegression from pyspark.ml.feature import VectorAssembler from pyspark.ml import Pipeline from pyspark.ml.evaluation import RegressionEvaluator
1. Podziel zbiór na dane uczące i testowe
df_train,df_test = df2.randomSplit([0.7,0.3],seed=1)
2. Skonfiguruje VectorAssembler i LinearRegression i umieść obiekty w ciągu przetwarzania pipeline
pipeline = Pipeline(stages=[va,lr])
3. Przeprowadź budowę modelu i predykcję dla zbioru uczącego i testowego
model = pipeline.fit(df_train) df_train_pred = model.transform(df_train) df_test_pred = model.transform(df_test)
4. Wyświetl metryki rmse i r2 dla zbiorów treningowego i testowego
evaluator = RegressionEvaluator() \ .setLabelCol("price") \ .setPredictionCol("prediction") \ .setMetricName("rmse"); rmse = evaluator.evaluate(df_train_pred);
5. Czy wyniki zależą od wielkości zbioru uczącego? Podziel zbiór w proporcji [1-test_size,test_size]? Poeksperymentuj z różnymi wartościami.
Wypróbuj formułę: test_size = 1-k*len(df2.columns)/count, gdzie count = df2.count()
Sprawdź dla k=1,2,3…10,20,30,…100,200,300
Ile danych (w stosunku do liczby atrybutów) potrzeba do nauczenie modelu, aby uzyskać akceptowalne rezultaty?
Przedstaw wyniki w formie tabelki
3.2 Funkcje
1. Zaimplementuj następujące funkcje
def evaluate_metrics(df,metrics=['r2','rmse','mse','mae'],label_col='price',prediction_col='prediction'): """ Funkcja oblicza metryki regresji na podstawie zbioru danych zawierającego prawdziwe wartosci etykiet i wartości przewidywane :param df: Dataset<Row> wejściowy zbiór danych :param metrics: lista metryk do obliczenia :param label_col: nazwa kolumny z wartosciami ściowymi :param prediction_col: nazwa kolumny zawierającej przewidywane wartosci :return: słownik zawierajacy pary (nazwa_metryki,wartosc) """
def train_and_test(df,lr=LinearRegression() .setMaxIter(100) .setRegParam(3.0) .setElasticNetParam(0.5) .setFeaturesCol("features") .setLabelCol("price")): """ Funkcja (1) dzieli zbiór danych na ``df_train`` oraz ``df_test`` (2) tworzy ciag przetwarzania zawierający ``VectorAssembler`` i przekazaną jako parametr konfiguracje algorytmu regresji (3) buduje model i dokonuje predykcji dla ``df_train`` oraz ``df_test`` (4) wyświetla metryki :param df: wejściowy zbiór danych :param lr: konfiguracja algorytmu regresji :return: model zwrócony przez ``pipeline.fit()`` """
2. Przeprowadź regresję
3. Wydrukuj równanie regresji na podstawie współczynników w zwróconym modelu
Wartość i-tego współczynnika (odpowiadającego i-tej kolumnie można odczytać za pomocą następującego kodu:
model.stages[1].coefficients[i]
Oczekiwany wynik typu:
price= + bedrooms * -49991.75843365818 + bathrooms * 55476.70050934714 + sqft_living * 104.96315420356594 + sqft_lot * 0.07232134546026013 + floors * 2232.279968637929 + waterfront * 537739.5601844544 + view * 57847.597444994964 + condition * 24601.336611537612 + grade * 97515.11069734246 + sqft_above * 96.13859631725865 + sqft_basement * 73.33408127400288 + yr_built * -2755.7047349795776 + yr_renovated * 19.590837790620963 + zipcode * -667.2478851292814 + lat * 592243.1919793531 + long * -234232.13414446148 + sqft_living15 * 19.225301468618166 + sqft_lot15 * -0.4392023871115651 + unixdate * 0.0013054659138663496 + 11531943.585431337
4. Przeanalizuj wpływ kilku atrybutów na cenę. Na przykład:
- O ile rośnie cena wraz ze wzrostem powierzchni o 1 m2
- O ile są droższe domy przy linii brzegowej
- Czy ceny zmieniały się z czasem. O ile miesięcznie?
Aby wpływ atrybutów ocenić należy uwzględnić zakresy wartości… Przykłady zapytań
df2.agg({'bathrooms':'max'}).collect()[0][0] df2.agg({'bathrooms':'median'}).collect()[0][0] df2.agg({'sqft_lot':'mean'}).collect()[0][0] df2.agg({'bedrooms':'min'}).collect()[0][0]
3.3 Walidacja krzyżowa
1. Poniższy kod przeprowadza walidację krzyżową wykonując ją na zbiorze treningowym. Podczas walidacji obliczana jest jedna metryka przekazana jako parametr
from pyspark.ml.tuning import ParamGridBuilder, CrossValidator cols = df2.columns cols.remove('price') va=VectorAssembler().setInputCols(cols).setOutputCol("features") lr=LinearRegression()\ .setMaxIter(100)\ .setRegParam(1) \ .setElasticNetParam(0.5) \ .setFeaturesCol("features")\ .setLabelCol("price") pipeline = Pipeline(stages=[va,lr]) evaluator = RegressionEvaluator(metricName='r2',labelCol='price') crossval = CrossValidator(estimator=pipeline, estimatorParamMaps = ParamGridBuilder().build(), evaluator=evaluator, numFolds=5) # Train the model using cross-validation df_train,df_test = df2.randomSplit([0.9, 0.1],seed=1) cvModel = crossval.fit(df_train) print(f'AVG r2 {cvModel.avgMetrics}')
2. Użyj model cvModel do predykcji i obliczania wyników dla zbioru uczącego i testowego.
Czy poprawne jest, że wartość r2 dla całego zbioru jest inna niż wartość średnia uzyskana przy walidacji krzyżowej?
3.4 Grid search
Walidacja krzyżowa służy do doboru hiperparametrów algorytmu.
1. Definiując konfigurację LinearRegression pomiń regParam i elasticNetParam
2. Zdefiniuj siatkę parametrów
paramGrid = ParamGridBuilder() \ .addGrid(lr.regParam, [0.1, 1, 3,5]) \ .addGrid(lr.elasticNetParam, [0, 0.5, 1]) \ .build()
i skonfiguruj walidację krzyżową
crossval = CrossValidator(estimator=pipeline, estimatorParamMaps=paramGrid, evaluator=evaluator, numFolds=5,parallelism=4)
3. Wykonaj walidację krzyżową na 90% danych i wyznacz najlepszy model (w świetle metryki r2)
Tym razem instrukcja print(f'AVG r2 {cvModel.avgMetrics}') wypisze listę 3*3=9 wartości.
bestModel = cvModel.bestModel
Wypisz jego parametry: regParam oraz elasticNetParam
4. Oblicz metryki dla zbioru testowego (pozostawione 10% danych)
4. Analiza cech
4.1 Czy atrybuty są skorelowane
1. Wyznacz macierz korelacji
n = len(df2.columns) rs = np.eye(n) #oblicz elementy macierzy za pomocą instrukcji r = df2.stat.corr(df2.columns[i],df2.columns[j])
2. Wydrukuj macierz
import itertools import matplotlib.pyplot as plt def plot_matrix(cm, labels, normalize=False, title='', cmap=plt.cm.Blues): fig = plt.figure(figsize=(10,10)) ax=fig.add_subplot(111) ax.matshow(cm, interpolation='nearest', cmap=cmap) plt.title(title) # plt.colorbar() tick_marks = np.arange(len(labels)) plt.xticks(tick_marks, labels, rotation=90) ax.set_xticks(tick_marks) ax.set_yticks(tick_marks) ax.set_xticklabels(labels) # ax.set_yticklabels(['']+labels) ax.set_yticklabels(labels) fmt = '.2f' #if normalize else 'd' thresh = 0.5 for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])): plt.text(j, i, format(cm[i, j], fmt), horizontalalignment="center", color="white" if cm[i, j] > thresh else "black") plt.tight_layout() plt.show() plot_matrix(rs,labels=df2.columns)
3. Usuń kolumny słabo skorelowane z ceną (ewentualnie mocno skorelowane z innymi zmiennymi objaśniającymi), a następnie przeprowadź regresję i wyświetl wyniki
df3 = df2.drop(?,?,?,?,...) train_and_test(df3)
4.2 Transformacja logarytmiczna ceny
4.2.1 Wstępne i końcowe przetwarzanie danych
1. Przeanalizuj wykresy. Który z wykresów zmiennej objaśnianej jest bliższy założeniom regresji liniowej?
plt.hist(df2.toPandas()['price'],bins=50) plt.show() plt.hist(np.log(df2.toPandas()['price']),bins=50) plt.show()
2. Dodaj kolumnę logprice zawierającą wynik wyrażenia log(price) Wynik zapisz w df3
3. Wyznacz i wyświetl macierz korelacji
Czy atrybuty są mocniej skorelowane z logprice?
4 Napisz i przetestuj kod (lub funkcję train_and_test_log), która
- Przeprowadzi regresję na atrybucie
logprice - Dokona predykjci dla zbioru treningowego i tetsowego
- Doda do nich kolumnę
exp_predjako wynikexp(prediction)oraz odtworzy oryginalną cenę - Obliczy metryki i wypisze ich wartości
4.2.2 Zastosowanie uogólnionego modelu liniowego (Generalized Linear Model)
Rozwiazanie jest analogiczne, jak przy regresji logistycznej, gdzie funkcją wiążącą jest $$logit(p)=ln(\frac{p}{1-p})$$
ale w tym przypadku funkcją wiążącą jest po prostu $ln$, czyli dokonujemy regresji dla
$$ln(y)=w^Tx$$
Przetestuj poniższą konfigurację algorytmu. Jakie były wyniki?
from pyspark.ml.regression import GeneralizedLinearRegression glr = GeneralizedLinearRegression(family="gaussian", link="log", maxIter=100, regParam=0.1, featuresCol="features", labelCol="price") df3 = df2.drop(....)
4.3 Variance Inflation Factor
Variance Inflation Factor (VIF) to miara pozwalająca określić stopień zależności liniowej pomiędzy wieloma zmiennymi objasniającymi. Patrz: https://www.investopedia.com/terms/v/variance-inflation-factor.asp
Wartość VIF dla poszczególnych zmiennych $X = {x_1,\ldots,x_n}$ określa się empirycznie przez
- Przeprowadzenie regresji $X_i = f(X \setminus {x_i})$ - zależność atrybutu $x_i$ od pozostałych atrybutów
- Wyznaczenie wartości współczynnika determinacji $r^2_i$
- Obliczenie $VIF(x_i)=\frac{1}{1-r^2_i}$
Wartości VIF powyżej 5 wskazują na wielokrotną liniową zależność i taka zmienna jest zazwyczaj usuwana.
1. Napisz funkcję
def compute_vif(df,label_col): """ Funkcja przeprowadza regresję na całym zbiorze danych, traktując label_col, jako zmienną objasnianą. Czyli konfigurując ''Vector Assembler'' pomija tę kolumnę. buduje model regresji i odczytuje wartośc współczynnika determinacji ''r2'' z model.summary. Następnie zwraca 1/(1-r2) Uwaga, jeżeli r2==1, nelezy odjąć od r2 niewielką wartośc, np. 1e-10 :param df: wejściowy zbiór danych :param label_col: nazwa atrybut, dla którego należy obliczyć VIF :return: wartość parazmetru VIF """
2. Oblicz wartości VIF, a następnie przedstaw je w postaci tabelki (np. Pandas Dataframe posortowanej według wartości VIF malejąco)
df3 = df2.drop('price') vifs = [] for f in df3.columns: vifs.append((f,compute_vif(df3,f))) print(vifs)
3. Przeprowadź regresję po odrzuceniu współliniowych atrybutów i podaj wyniki
4. Przeprowadź regresję pozostawiając jeden ze współliniowych atrybutów (sqft_living)
4.4 Normalizacja cech
1. Napisz funkcję dodającą etap skalowania cech do ciagu przetwarzania pipeline
from pyspark.ml.feature import StandardScaler def train_and_test_scaled(df,lr=LinearRegression() .setMaxIter(100) .setRegParam(3.0) .setElasticNetParam(0.5) .setFeaturesCol("features_scaled") .setLabelCol("price"),apply_normalization = False): """ Funkcja konfiguruje ciąg przetwarzania obejmujący trzy etapy: VectoAssembler, StandardScaler, LinearRegression param: df param: lr return: model """
2. Przetestuj jej działanie
3. Wydrukuj równanie regresji dla przeskalowanych zmiennych
Czy skalowanie ma wpływ na działanie algorytmu? W przypadku OLS nie. W przypadku regularyzacji tak. Zastanów się dlaczego?
5. Cechy wielomianowe
5.1 Czy lokalizacja domów ma wpływ na cenę?
Jeżeli chcesz, możesz zainstalować dodatkowe biblioteki i wyświetlić interaktywną mapę…
!pip install geopandas folium mapclassify
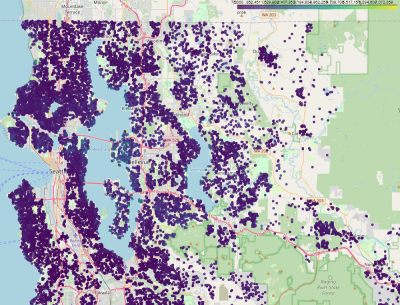
pdf= df2.toPandas() import geopandas as gpd gdf = gpd.GeoDataFrame(pdf, geometry=gpd.GeoSeries.from_xy(pdf['long'], pdf['lat']), crs=4326) gdf.explore('price')
Różnice nie są szczególnie widoczne, ponieważ skala obejmuje domy od najtańszych (75000) do najdroższych (7700000), przy medianie 45000
df2.agg({'price':'min'}).collect()[0][0] df2.agg({'price':'max'}).collect()[0][0]
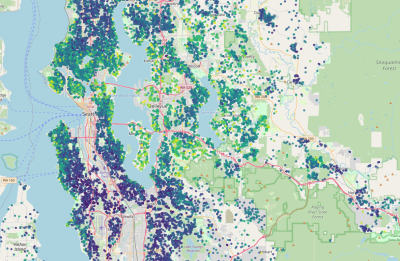
Ograniczenie danych do kwantyla 0.95 pozwala lepiej zobrazować zależności od położenia
gdf[gdf.price<=gdf.price.quantile(.95)].explore('price')
Dodamy cechy wielomianowe dla długości i szerokości geograficznej
1. Dodaj kolumny:
- 'lat_2' zawierającą wartości wyrażenia
lat*lat - 'long_2' zawierającą wartości wyrażenia
long*long - 'lat_long' zawierającą wartości wyrażenia
lat*long
i przeprowadź regresję. Jakie były wyniki?
2. Wydrukuj równanie regresji.
Jaką krzywą jest opisana zależność między lat i long
5.2 Cechy wielomianowe dla wszystkich atrybutów
1. Zaimplementuj funkcję dokonującą ekspansji wielomianowej dla wszystkich atrybutów
from pyspark.ml.feature import MinMaxScaler def train_and_test_scaled_polynomial_features(df,lr=LinearRegression() .setMaxIter(100) .setRegParam(3.0) .setElasticNetParam(0.5) .setFeaturesCol("features_poly") .setLabelCol("price")): """ (1) Buduje ciąg przetwarzania obejmujący VectorAssembler, MinMaxScaler, PolynomialExpansioni lr (2) Dzieli zbiór na treningowy i testowy (3) Przeprowadza regresje i drukuje metryki dla zbioru treningowego i testowego param: df - zbiór danych param: lr - algorytm regresji returns: model pipeline """
2. Przetestuj funkcję. Czy wyniki poprawiły się?
5.3 Inne algorytmy regresji
Przetestuj funkcję train_and_test_scaled_polynomial_features dla innych algorytmów regresji. Który osiągnął najlepsze rezultaty (przyjmując jako kryterium r2 na zbiorze testowym).
from pyspark.ml.regression import DecisionTreeRegressor from pyspark.ml.regression import RandomForestRegressor from pyspark.ml.regression import GBTRegressor for r in [DecisionTreeRegressor(),RandomForestRegressor(),GBTRegressor()]: print(f'=== {r.__class__.__name__} ===')