Wyrażenia matematyczne

Podczas laboratorium zaimplementujemy kilka klas pozwalających na reprezentację prostych wyrażeń matematycznych (funkcji jednej lub kilku zmiennych) jako grafów. Podobna reprezentacja jest rdzeniem funkcji oferowanych na przykład przez https://live.sympy.org/ lub https://www.derivative-calculator.net/. Nie będziemy jednak “parsowali” wyrażeń, czyli budowali grafowej reprezentacji na podstawie specyfikacji tekstowej. Zamiast tego, wyrażenia będą budowane za pomocą odpowiednio skonstruowanego kodu.

Założona funkcjonalność:

• budowa wyrażeń
• obliczanie wartości wyrażeń/funkcji dla różnych wartości zmiennych
• wydruk wyrażeń
• symboliczne obliczanie pochodnych [opcjonalnie]

Przeanalizujmy wyrażenie $ 2x^3 + x^2 -2x + 7 $

Jego elementami są:

• stałe (np 2 i 7)
• zmienne (x)
• funkcja potęgowa ($x^3$, $x^2$) – Power(arg,p)
• operacja mnożenia Prod(args…)
• operacja dodawania Sum(args…)

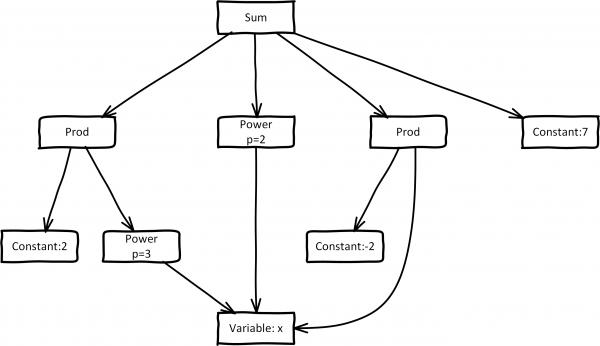
Wyrażenie $ 2x^3 + x^2 -2x + 7 $ może być zapisane jako Sum(Prod(2,Power(x,3)),Power(x,2),Prod(-2,x),7). Zakładając, że każdy z tych elementów będzie obiektem, otrzymamy reprezentację w postaci acyklicznego grafu, jak na poniższym rysunku. Węzłami grafu są stałe, zmienne, operacje i funkcje, natomiast krawędzie odpowiadają argumentom poszczególnych operacji.

W zasadzie jest to drzewo, którego liśćmi są zmienne i stałe. Ponieważ zmienne mogą powtarzać się, liście będące zmiennymi zostały złączone

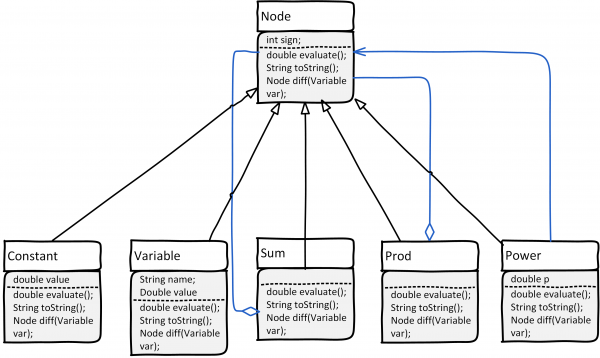
Zaimplementujemy więc klasy, jak na poniższym diagramie i dodamy wspólnego przodka, abstrakcyjną klasę Node. Niebieskie linie to asocjacje/agregacje łączące węzły nadrzędne (opreacje, funkcje) i ich argumenty.

• Argumentem Power jest jakieś wyrażenie, czyli Node.
• Sum może mieć więcej argumentów, stąd agregacja elementów Node
• Prod (product) to iloczyn większej liczby czynników Node

abstract public class Node {
    int sign=1;
    Node minus(){
        sign = -1;
        return this;
    }
    Node plus(){
        sign = 1;
        return this;
    }
    int getSign(){return sign;}
 
    /**
     * Oblicza wartość wyrażenia dla danych wartości zmiennych
     * występujących w wyrażeniu
     */
    abstract double evaluate();
 
    /**
     *
     * zwraca tekstową reprezentację wyrażenia
     */
    public String toString(){return "";}
 
    /**
     * 
     * Zwraca liczbę argumentów węzła
     */
    int getArgumentsCount(){return 0;}
 
}

W klasie Node wprowadzono atrybut sign znak, dziedziczony przez klasy potomne. Potraktujmy to następująco. Załóżmy, że reprezentacją tekstową węzła jest abcd

• jeśli sign<0 reprezentacją tekstową będzie -(abcd) [w nawiasach]
• jeśli sign>=0 będzie to po prostu abcd [bez nawiasów]

public class Constant extends Node {
    double value;
    Constant(double value){
        this.sign = value<0?-1:1;
        this.value = value<0?-value:value;
    }
 
 
    @Override
    double evaluate() {
        return sign*value;
    }
 
    @Override
    public String toString() {
        String sgn=sign<0?"-":"";
//        return sgn+Double.toString(value);
        DecimalFormat format = new DecimalFormat("0.#####",new DecimalFormatSymbols(Locale.US));
        return sgn+format.format(value);
    }
}

Stosując DecimalFormat pozbędziemy się niepotrzebnych zer na końcu wartości double.

Klasa Variable reprezentuje zmienną, która może być użyta w wyrażeniach.

public class Variable extends Node {
    String name;
    Double value;
    Variable(String name){
        this.name = name;
    }
    void setValue(double d){
        value = d;
    }
 
 
    @Override
    double evaluate() {
         return sign*value;
    }
 
 
    @Override
    public String toString() {
        String sgn=sign<0?"-":"";
        return sgn+name;
    }
 
}

Power jest jedyną zaimplementowaną funkcją. Zauważmy, że $Power(x,-1)=\frac{1}{x}$. Argumentem Power nie musi być pojedyncza zmienna. Może to być np.: Power(Sum(x,2),-2), czyli $\frac{1}{(x+2)^2}$

W kodzie pokazano przykładową implementację toString() z próbą wstawienia nawiasów w takich przypadkach, jak $-(-x^5)$ lub $(x+1)^2$

public class Power extends Node {
    double p;
    Node arg;
    Power(Node n,double p){
        arg = n;
        this.p = p;
    }
 
    @Override
    double evaluate() {
        double argVal = arg.evaluate();
        return Math.pow(argVal,p);
    }
 
 
    int getArgumentsCount(){return 1;}
 
 
    @Override
    public String toString() {
        StringBuilder b = new StringBuilder();
        if(sign<0)b.append("-");
        int argSign = arg.getSign();
        int cnt = arg.getArgumentsCount();
        boolean useBracket = false;
        if(argSign<0 ||cnt>1)useBracket = true;
        String argString = arg.toString();
        if(useBracket)b.append("(");
        b.append(argString);
        if(useBracket)b.append(")");
        b.append("^");
        b.append(p);
        return b.toString();
    }
 
}

Klasa Sum jest wyrażeniem reprezentującą sumę argumentów. Zawiera listę węzłów List<Node> args = new ArrayList<>();

Teoretycznie, lista argumentów może liczyć 0,1,2,… elementów. Metoda add() dodaje składniki do listy

public class Sum extends Node {
 
    List<Node> args = new ArrayList<>();
 
    Sum(){}
 
    Sum(Node n1, Node n2){
        args.add(n1);
        args.add(n2);
    }
 
 
    Sum add(Node n){
        args.add(n);
        return this;
    }
 
    Sum add(double c){
        args.add(new Constant(c));
        return this;
    }
 
    Sum add(double c, Node n) {
        Node mul = new Prod(c,n);
        args.add(mul);
        return this;
    }
 
    @Override
    double evaluate() {
        double result =0;
        oblicz sumę wartości zwróconych przez wywołanie evaluate skłądników sumy
        return sign*result;
    }
 
    int getArgumentsCount(){return args.size();}
 
    public String toString(){
        StringBuilder b =  new StringBuilder();
        if(sign<0)b.append("-(");
 
        //zaimplementuj
 
        if(sign<0)b.append(")");
        return b.toString();
    }
 
 
}

Prod to iloczyn (ang. product). Reprezentuje wyrażenie będące iloczynem czynników. Metoda mul() dodaje czynnik do listy.

public class Prod extends Node {
    List<Node> args = new ArrayList<>();
 
    Prod(){}
 
    Prod(Node n1){
        args.add(n1);
    }
    Prod(double c){
        wywołaj konstruktor jednoargumentowy przekazując new Constant(c)
    }
 
    Prod(Node n1, Node n2){
        args.add(n1);
        args.add(n2);
    }
    Prod(double c, Node n){
        wywołaj konstruktor dwuargumentowy
    }
 
 
 
    Prod mul(Node n){
        args.add(n);
        return this;
    }
 
    Prod mul(double c){
        ???
    }
 
 
    @Override
    double evaluate() {
        double result =1;
        // oblicz iloczyn czynników wołąjąc ich metodę evaluate
        return sign*result;
    }
    int getArgumentsCount(){return args.size();}
 
 
    public String toString(){
        StringBuilder b =  new StringBuilder();
        if(sign<0)b.append("-");
        // ...
        zaimplementuj
        return b.toString();
    }
 
 
}

    static void buildAndPrint(){
        Variable x = new Variable("x");
        Node exp = new Sum()
                .add(2.1,new Power(x,3))
                .add(new Power(x,2))
                .add(-2,x)
                .add(7);
        System.out.println(exp.toString());
 
    }

Oczekiwany wynik: 2.1*x^3 + x^2 + (-2)*x + 7

    static void buildAndEvaluate(){
        Variable x = new Variable("x");
        Node exp = new Sum()
                .add(new Power(x,3))
                .add(-2,new Power(x,2))
                .add(-1,x)
                .add(2);
        for(double v=-5;v<5;v+=0.1){
            x.setValue(v);
            System.out.printf(Locale.US,"f(%f)=%f\n",v,exp.evaluate());
        }

Sprawdź, jakie są pierwiastki?

    static void defineCircle(){
        Variable x = new Variable("x");
        Variable y = new Variable("y");
        Node circle = new Sum()
                .add(new Power(x,2))
                .add(new Power(y,2))
                .add(8,x)
                .add(4,y)
                .add(16);
        System.out.println(circle.toString());
 
        double xv = 100*(Math.random()-.5);
        double yv = 100*(Math.random()-.5);
        x.setValue(xv);
        y.setValue(yv);
        double fv = circle.evaluate();
        System.out.print(String.format("Punkt (%f,%f) leży %s koła %s",xv,yv,(fv<0?"wewnątrz":"na zewnątrz"),circle.toString()));
}

Znajdź i wypisz 100 punktów leżących wewnątrz okręgu…. Oczywiście napisz kod, który je znajduje

Zadanie do realizacji w domu.

Pochodna wyrażenia jest również wyrażeniem… Dodajmy metodę diff() w klasie Node

    abstract Node diff(Variable var);

Dodajmy jeszcze metodę

    abstract boolean isZero();

która będzie służyła do optymalizacji wywołań (pomijamy wyrażenia o wartości 0).

Zawsze pochodną stałej jest zero.

    @Override
    Node diff(Variable var) {
        return new Constant(0);
    }

Pochodna $\frac{d}{dx}(x)=1$, natomiast $\frac{d}{dx}(y)=0$

    Node diff(Variable var) {
        if(var.name.equals(name))return new Constant(sign);
        else return new Constant(0);
    }

Z definicji $\frac{d}{dx}(x^n)=nx^{n-1}$, ale tak naprawdę powinniśmy potraktować to jako złożenie funkcji $Power(arg(x)),p$, stąd

$$\frac{d}{dx}(arg(x)^n) = n\cdot arg(x)^{n-1}\cdot \frac{d}{dx}arg(x)$$

    Node diff(Variable var) {
        Prod r =  new Prod(sign*p,new Power(arg,p-1));
        r.mul(arg.diff(var));
        return r;
    }

Pochodna sumy jest sumą pochodnych. Najprostsza implementacja jest podana poniżej.

    Node diffVanilla(Variable var) {
        Sum r = new Sum();
        for(Node n:args){
            r.add(n.diff(var));
        }
        return r;
    }

Niestety, dużo pochodnych składowych będzie zerowych. Stąd propozycja usprawnienia przez sprawdzenie przed dodaniem, czy wyrażenie nie jest zerem.

Ogólny algorytm iloczynu jest podany np. tu https://en.wikipedia.org/wiki/Product_rule. Zauważmy, że stosuje się to także do funkcji stałych (w projekcie Constant):

$$\frac{d}{dx}(2\cdot f(x))=\frac{d}{dx}(2)\cdot f(x) + 2\cdot \frac{d}{dx}f(x)$$ $$=0\cdot f(x) + 2\cdot \frac{d}{dx} f(x)$$

Stąd najprostsza implementacja ma postać:

    Node diffVanilla(Variable var) {
        Sum r = new Sum();
        for(int i=0;i<args.size();i++){
            Prod m= new Prod();
            for(int j=0;j<args.size();j++){
                Node f = args.get(j);
                if(j==i)m.mul(f.diff(var));
                else m.mul(f);
            }
            r.add(m);
        }
        return r;
    }

Niestety, w jej wyniku może powstać sporo wyrażeń zerowych…

static void diffPoly() {
        Variable x = new Variable("x");
        Node exp = new Sum()
                .add(2,new Power(x,3))
                .add(new Power(x,2))
                .add(-2,x)
                .add(7);
        System.out.print("exp=");
        System.out.println(exp.toString());
 
        Node d = exp.diff(x);
        System.out.print("d(exp)/dx=");
        System.out.println(d.toString());
 
    }

Wynik

exp=2*x^3 + x^2 + (-2)*x + 7
d(exp)/dx=0*x^3 + 2*3*x^2*1 + 2*x^1*1 + 0*x + (-2)*1 + 0

    static void diffCircle() {
        Variable x = new Variable("x");
        Variable y = new Variable("y");
        Node circle = new Sum()
                .add(new Power(x,2))
                .add(new Power(y,2))
                .add(8,x)
                .add(4,y)
                .add(16);
        System.out.print("f(x,y)=");
        System.out.println(circle.toString());
 
        Node dx = circle.diff(x);
        System.out.print("d f(x,y)/dx=");
        System.out.println(dx.toString());
        System.out.print("d f(x,y)/dy=");
        Node dy = circle.diff(y);
        System.out.println(dy.toString());
 
    }

Wynik

f(x,y)=x^2 + y^2 + 8*x + 4*y + 16
d f(x,y)/dx=2*x^1*1 + 2*y^1*0 + 0*x + 8*1 + 0*y + 4*0 + 0
d f(x,y)/dy=2*x^1*0 + 2*y^1*1 + 0*x + 8*0 + 0*y + 4*1 + 0

Pomijaj przy sumowaniu wyrażenia zerowe Przed utworzeniem węzłów Sum i Prod umieść wyrażenia na listach.

• Jeżeli lista jest pusta, zwróć new Constant(0)
• Jeżeli lista zawiera jeden element, po prostu zwróć go

Wynik dla circle:

f(x,y)=x^2 + y^2 + 8*x + 4*y + 16
d f(x,y)/dx=2*x^1*1 + 8*1
d f(x,y)/dy=2*y^1*1 + 4*1

Dodaj metodę simplify() , która zastąpi iloczyn stałych pojedynczą stałą. Spłaszcz strukturę Constant()*Product(args) do pojedynczego iloczynu.

exp=2*x^3 + x^2 + (-2)*x + 7
d(exp)/dx=6*x^2 + 2*x^1 + (-2)
f(x,y)=x^2 + y^2 + 8*x + 4*y + 16
d f(x,y)/dx=2*x^1 + 8
d f(x,y)/dy=2*y^1 + 4

Dodaj klasy odpowiadające innym funkcjom, np. exp(), log(), sin(), cos(), itd… A w przyszłości może uda się rozwinąć program do postaci podobnej do https://www.derivative-calculator.net/