Laboratorium 7 - przewidywanie liczby wypożyczonych rowerów

Kontynuujemy regresję. Będziemy przetwarzali zbiór danych dotyczących wypożyczeń rowerów w okresie dwóch lat. Wykorzystamy środowisko PySpark (obraz dockera spark-jupyter z zajęć 5) ale bez klastra. Spark będzie uruchamiany w konfiguracji standalone. Użyj środowiska jupyter-lab

1. Uruchom obraz spark-jupyter

docker run -it --rm -v ".:/opt/spark/work-dir"  -p 4040:4040  -p 8888:8888 -p 443:443 --network spark-network spark-jupyter /bin/bash

2. W konsoli kontenera wydaj komendę startującą serwer notatników jupyter-lab

sudo --preserve-env jupyter-lab  --ip=0.0.0.0 --allow-root --IdentityProvider.token='pyspark'

3. Edytuj kod w notatniku…

!wget https://dysk.agh.edu.pl/s/G6ZNziBRbEEcMeN/download/Bike-Sharing-Dataset.zip -O Bike-Sharing-Dataset.zip
!unzip Bike-Sharing-Dataset.zip
!cat Readme.txt

Po rozpakowaniu przeczytaj opis zbioru danych.

1. Utwórz lokalną sesję Sparka i wczytaj dane.

import pyspark
from pyspark.sql import SparkSession
from pyspark.sql.functions import *
spark = SparkSession.builder.appName("BikerRental").master("local[*]").getOrCreate()

df = spark.read.csv('day.csv', header=True, inferSchema=True)
df.show(5)
df.printSchema()

Sprawdź, czy typ danych kolumny z datą został poprawnie zidentyfikowany

2. Przekonwertuj zbiór do pandas.DateFrame i wyświetl histogramy.

import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (15,10)
pdf =df.toPandas()

3. Wyświetl wykres zależności cnt, registered i casual do daty date

dates = df.select('dteday').rdd.flatMap(lambda x:x).collect()
...

1. Napisz następujące funkcje

from pyspark.ml.regression import LinearRegression
from pyspark.ml.feature import VectorAssembler
from pyspark.ml import Pipeline
from pyspark.ml.evaluation import RegressionEvaluator
 
def evaluate_metrics(df,metrics=['r2','rmse','mse','mae'],label_col='cnt',prediction_col='prediction'):
    """
    Funkcja oblicza metryki regresji na podstawie zbioru danych zawierającego prawdziwe wartosci etykiet 
    i wartości przewidywane
    :param df: Dataset<Row> wejściowy zbiór danych
    :param metrics: lista metryk do obliczenia
    :param label_col: nazwa kolumny z wartościami wyjściowymi
    :param prediction_col: nazwa kolumny zawierającej przewidywane wartości
    :return: słownik zawierający pary (nazwa_metryki, wartość) 
    """

Będziemy dokonywali predykcji kolumny cnt. Ustaw ją jako parametr lr.

def train_and_test(df,lr=LinearRegression(maxIter=100,regParam=3.0,elasticNetParam=0.5)):
    """
    Funkcja (1) dzieli zbiór danych na ``df_train`` oraz ``df_test`` 
    (2) tworzy ciąg przetwarzania zawierający ``VectorAssembler`` 
    i  przekazaną jako parametr konfiguracje algorytmu regresji
    (3) buduje model i dokonuje predykcji dla ``df_train`` oraz ``df_test``
    (4) wyświetla metryki
    :param df: wejściowy zbiór danych
    :param lr: konfiguracja algorytmu regresji
    :return: model  zwrócony przez ``pipeline.fit()``
    """

2. Przekonwertuj datę do postaci numerycznej za pomocą funkcji unix_timestamp(). Zakładamy, że kolumna ma mieć nazwę unixdate, z identyfikator przetworzonego zbioru danych df2. Usuń kolumny z którymi zmienna wyjściowa jest powiązana liniową zależnością.

3. Wywołaj funkcję train_and_test(). Przykładowy wynik:

Train: r2=0.8075845429647183 rmse=842.8329062164518 mse=710367.3078012702 mae=634.2406059893968
Test: r2=0.7728820606921822 rmse=934.713606071121 mse=873689.5253744789 mae=660.1099130393472

1. Wykonaj 5-krotną walidację krzyżową przeszukując siatkę parametrów algorytmu regresji. Na przykład:

paramGrid = ParamGridBuilder() \
    .addGrid(lr.regParam, [0.1, 0.5, 1, 2, 3, 5, 10]) \
    .addGrid(lr.elasticNetParam, [0.0, 0.25, 0.5, 0.75, 1.0]) \
    .build()

2. Wydrukuj parametry znalezionego najlepszego modelu

bestModel = cvModel.bestModel
print("Best model parameters:")
print("regParam:", bestModel.stages[-1].getRegParam())
print("elasticNetParam:", bestModel.stages[-1].getElasticNetParam())

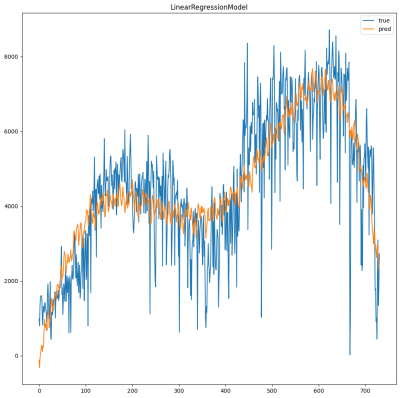
3. Wyświetl wykresy rzeczywistych i przewidywanych wartości. Obejrzyj wyniki dla różnych przedziałów.

import numpy as np
 
def plot(df,model,start=0,end=-1):
    if end == -1:
        end = df.count()
    x = np.arange(start,end)
    y = df.select('cnt').rdd.flatMap(lambda x:x).collect()
    df_pred = model.transform(df)
    y_pred = df_pred.select('prediction').rdd.flatMap(lambda x:x).collect()  
    plt.plot(x,y[start:end],label='true')
    plt.plot(x,y_pred[start:end],label='pred')
    plt.legend()
    plt.title(model.stages[-1].__class__.__name__)
    plt.show()
 
plot(df2,bestModel,start=,end=)

1. Porównaj najlepszą znalezioną konfigurację z innymi algorytmami regresji

from pyspark.ml.regression import DecisionTreeRegressor
from pyspark.ml.regression import RandomForestRegressor
from pyspark.ml.regression import GBTRegressor
 
for r in [LinearRegression(maxIter=,regParam=,elasticNetParam=),DecisionTreeRegressor(),RandomForestRegressor(),GBTRegressor()]:
    print(f'=== {r.__class__.__name__} ===')

2 Narysuj wykres dla najlepszego algorytmu (według miary r2 na zbiorze testowym)

1. Dla wszystkich kolumn df2 za wyjątkiem cnt:

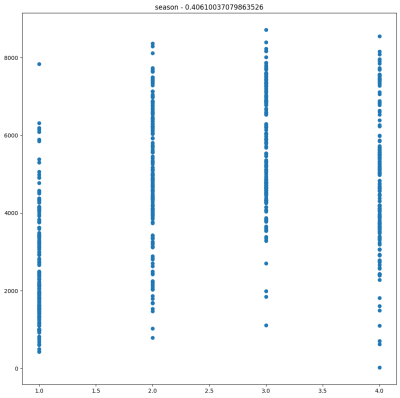
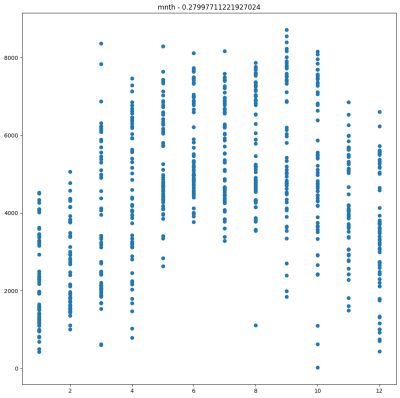
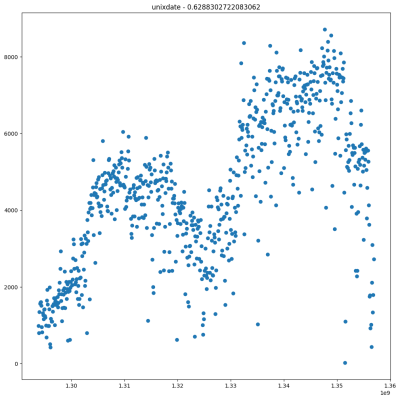
• Oblicz współczynnik korelacji Pearsona ze zmienną objaśnianą: r = df2.stat.corr(col,'cnt')
• Wyświetl wykres typu scatter plot pokazujący zależność pomiędzy daną kolumną a cnt

2. Obejrzyj wykresy. Czy współczynnik korelacji zmieniłby się, gdyby zmienić kolejność miesięcy? W takim przypadku zastosujemy konwersję one-hot.

Uwaga. Nie ma sensu stosować konwersji one-hot jeżeli atrybut ma dwie wartości.

3. Jak konwersja jest sugerowana w tym przypadku?

Konwersja one-hot zamienia atrybut dyskretny z $k$ wartościami $\{a_1,\dots,a_k\}$, na $k$ kolumn, w których umieszczane są zera i jedynki. Wartość $x'$ po konwersji jest ustalana jako

• $x'[i,j]=1$, jeżeli przed konwersją $x[i]=a_j$,
• $x'[i,j]=0$, jeżeli przed konwersją $x[i]\neq a_j$

1. Przetestuj, jak działa OneHotEncoder. Dodaje on jedną kolumnę, która jest rzadkim wektorem. Co więcej, standardowo dla $k$ atrybutów tworzy wektory $k-1$ elementowe. https://spark.apache.org/docs/latest/api/java/org/apache/spark/ml/feature/OneHotEncoder.html

Stosowany później VectorAssembler łączy wektory i pojedyncze wartości w jeden wektor.

from pyspark.ml.feature import OneHotEncoder
 
encoder = OneHotEncoder(inputCol="weekday", outputCol="categoryVec")
model = encoder.fit(df2)
df_encoded = model.transform(df2)
df_encoded.show()

2. Napisz funkcję:

from pyspark.ml.feature import OneHotEncoder
 
def encode_one_hot(df,col):
    """
    Funkcja przekształca wybraną kolumny do postaci one-hot - tablicy wartości 0/1
    :param df: Dataset<Row> wejściowy zbiór danych
    :param col: kolumna do konwersji one hot
    :return: zbiór danych z kolumną col przekształconą do postaci one-hot 
    """

3. Dokonaj za jej pomocą konwersji odpowiednich atrybutów

df3 = encode_one_hot(df3,'mnth')
df3 = ...

4 Dodaj także (jawnie, jako wyrażenia) cechy wielomianowe dla wybranych atrybutów. Jakiego stopnia? Parabola ma 1 garb, krzywa 3 stopnia 2 garby, itd…

5. Przetestuj i wyświetl wykres

model = train_and_test(df3,lr=)
plot(df3,model)

6. Powtórz testy dla innych algorytmów regresji

Interesuje nas zależność cnt od instance. W pierwszej części dobierzemy postać wielomianu aproksymującego trend, a w drugiej dodamy cechy okresowe..

1. Napisz funkcję

from pyspark.ml.feature import PolynomialExpansion
 
# Param for the ElasticNet mixing parameter, in range [0, 1]. For alpha = 0, the penalty is an L2 penalty. For alpha = 1, it is an L1 penalty.
 
def train_polynomial_features(df,lr=LinearRegression(),degree=2):
    """
    Funkcja przetwarza cały zbiór danych 
    (1) tworzy ciag przetwarzania zawierający ``VectorAssembler`` 
    z jedynym wejściowym atrybutem ``instance``, dalej ''PolynomialExpansion'' 
    i  przekazaną jako parametr konfiguracje algorytmu regresji
    (2) buduje model i dokonuje predykcji dla ``df``
    (3) wyświetla metryki za pomocą funkcji ``evaluate_metrics()``
    :param df: wejściowy zbiór danych
    :param lr: konfiguracja algorytmu regresji wielomianu (argument ``PolynomialExpansion``)
    :param degree: stopień wielomianu (argument PolynomialExpansion)
    :return: model  zwrócony przez ``pipeline.fit()``
    """

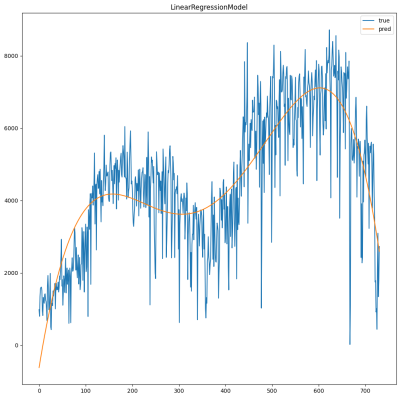
2. Dobierz parametry algorytmu

model = train_polynomial_features(df, lr = LinearRegression(maxIter=??,regParam=???,elasticNetParam=???),degree=??)
print(model.stages[-1].coefficients)
print('Iterations: ',model.stages[-1].summary.totalIterations)
plot(df,model)

Ustaw

• Bardzo małą wartość regParam
• Poeksperymentuj ze skrajnymi wartościami elasticNetParam (albo 0 albo 1) oraz skrajnymi wartościami maxIter (np. 10 i 100000)

Oczekiwany wynik:

Cechy okresowe można zidentyfikować:

• wyznaczając autokorelację (korelację przebiegu z przebiegiem przesuniętym o 1,2,3,4,… przedziały czasu
• analizując amplitudy częstotliwości po transformacji Fouriera

Jeśli chcesz, możesz zainstalować brakujące oprogramowanie…

!pip install seaborn
!pip install statsmodels

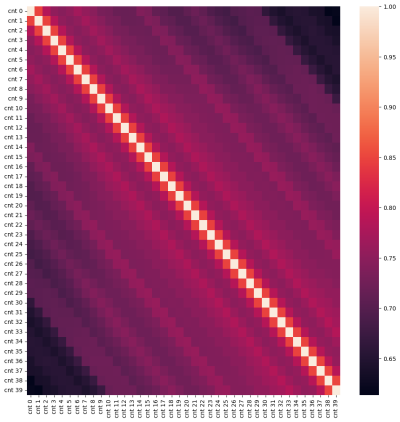
1. Macierz autokorelacji. Jaśniejsze paski wskazują na skorelowane wartości przesuniętych w czasie. Jakie to wartości?

import pandas as pd
pdf = df.toPandas()
shifted = [pd.DataFrame(data = pdf.cnt).shift(i) for i in range(40)]
for i in range(len(shifted)):
  shifted[i].columns=['cnt '+str(i)]
# print(shifted)
df_shifted = pd.concat(shifted,axis=1)
# df_shifted.head(20)
 
corr_mat = df_shifted.corr()
import seaborn as sn
plt.rcParams['figure.figsize'] = (12, 12)
sn.heatmap(corr_mat,xticklabels=df_shifted.columns,yticklabels=df_shifted.columns)

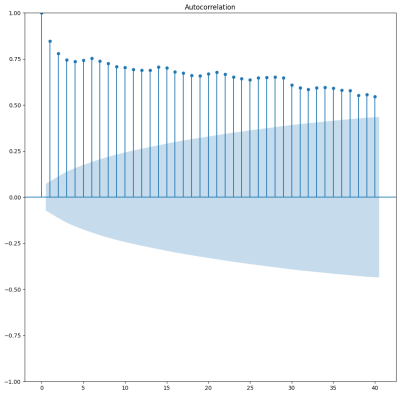
2. Wykres autokorelacji dla kolejnych okresów

from statsmodels.graphics.tsaplots import plot_acf
plot_acf(pdf.cnt,lags=40)

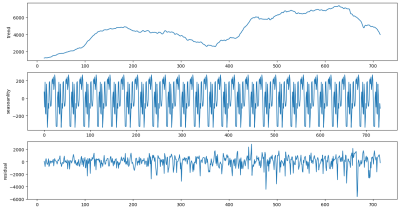
3. Dekompozycja na trend i cechy okresowe (sezonowe). W tym przypadku dla okresu 30 dni. Kod na podstawie: https://medium.com/analytics-vidhya/interpreting-acf-or-auto-correlation-plot-d12e9051cd14

from statsmodels.tsa.seasonal import seasonal_decompose
 
res = seasonal_decompose(pdf.cnt, model = "additive",period=30)
 
fig, (ax1,ax2,ax3) = plt.subplots(3,1, figsize=(15,8))
res.trend.plot(ax=ax1,ylabel = "trend")
res.seasonal.plot(ax=ax2,ylabel = "seasoanlity")
res.resid.plot(ax=ax3,ylabel = "residual")
plt.show()

Zastosujemy transformację Fouriera i zobaczymy, dla jakich częstotliwości mamy duże amplitudy?

import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack
 
y = pdf.cnt.to_numpy()
x = np.arange(-y.shape[0]//2,y.shape[0]//2)
 
yf = scipy.fftpack.fft(y)
 
N=y.shape[0]
 
yf = scipy.fftpack.fft(y)
yf[0]=0
xf = np.arange(1,40)
 
plt.scatter(xf, 2.0/N * np.abs(yf[1:40]))
plt.vlines(xf, np.zeros(39),2.0/N * np.abs(yf[1:40]))
plt.xticks(xf)
plt.show()

Dodamy cechy okresowe (pary funkcji ortogonalnych) postaci $cos(\frac{2\pi x}{T_i})$ oraz $sin(\frac{2\pi x}{T_i})$. Zmienna $x$ odpowiada atrybutowi instance natomiast $T_i \in \mathbf{T}$ jest jednym z wybranych okresów.

1. Dodaj cechy okresowe i zachowaj nazwy kolumn

periods=[...]
 
df3 = df
cols=[]
for k in periods:
    df3 = df3.withColumn(f'sin_{k}',expr(???))
    df3 = df3.withColumn(f'cos_{k}',expr(???))
    cols.append(f'sin_{k}')
    cols.append(f'cos_{k}')

2. Zaimplementuj poniższą funkcję

def train_polynomial_periodic_features(df,lr=LinearRegression(),degree=2,cols=[]):
     """
    Funkcja przetwarza cały zbiór danych 
    (1) tworzy ciag przetwarzania zawierający 
         (a) ``VectorAssembler`` z jedynym wejściowym atrybutem ``instance`` i wyjściową kolumną ``features``
         (b) ''PolynomialExpansion'' odpowiadający za cechy wielomianowe - tworzy kolumnę ``features_poly``
         (c) ``VectorAssembler`` z wejściowymi atrybutami przekazanymi przez listę cols uzupełniona o 
         ``features_poly`` z wyjściowa kolumną ``features_merged``
         (d) przekazaną jako parametr konfiguracje algorytmu regresji
    (2) buduje model i dokonuje predykcji dla ``df``
    (3) wyświetla metryki za pomocą funkcji ``evaluate_metrics()``
    :param df: wejściowy zbiór danych
    :param lr: konfiguracja algorytmu regresji wielomianu (argument ``PolynomialExpansion``)
    :param degree: stopień wielomianu (argument PolynomialExpansion)
    :param cols: kolumny z nazwami cech okresowych)
    :return: model
    """

3. Przetestuj i wyświetl wyniki

model = train_polynomial_periodic_features(df3,
                                           lr=LinearRegression(maxIter=???,regParam=???,elasticNetParam=???),
                                           degree=???,cols=cols)
print(model.stages[-1].coefficients)
print('Iterations: ',model.stages[-1].summary.totalIterations)
plot(df3,model)

Oczekiwana jest wartość r2 około 0.70.