PhD thesis – Paweł Potorski

On mixing interval maps

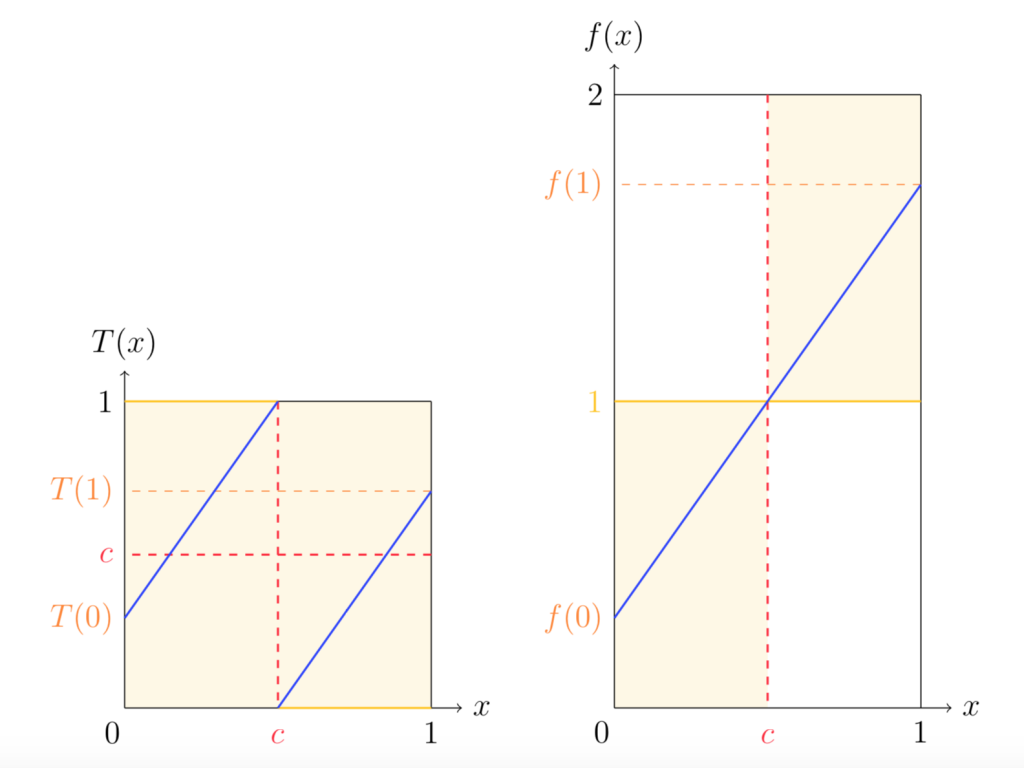
The simplest way to define an expanding Lorenz map $T_f:[0,1]\rightarrow [0,1]$ is to consider a continuous and strictly increasing generating map $f:[0,1]\to[0,2]$ satisfying $\inf f'>1$ ; then $T_f(x):= f(x) ({\text{mod }}1)$ (example of such a map is presented on graphs attached below). The presented study of those maps focused on investigating their topological properties and possible relationships between them.

Particular attention was paid to mixing property. Sufficient conditions for $T_f$ to be topologically mixing, using their Markov diagram, were provided. Using those conditions (and some additional assumptions) it was shown that $T_f$ is mixing for functions $f$ satisfying $\inf f^{\prime}\geq \sqrt[3]{2}$ . Based on the same assumption of $f$ all maps $T_f$ generated by an affine function $f$ were considered and the full characterization of parameters $(\beta,\alpha)$ leading to mixing in this case was given.

Moreover, it was shown that $T_f$ having a primary $n(k)$ -cycle cannot be mixing but can be transitive. Based on this result some parameters for which $T_f$ generated by an affine function $f$ is not mixing were pointed out. Additionally, not mixing but transitive cases were emphasized.

Furthermore, relations between $T_f$ being locally eventually onto, strongly locally eventually onto, mixing and renormalizable were considered.

One can find those results in
P. Oprocha, P. Potorski, P. Raith, Mixing properties in expanding Lorenz maps, Advances in Mathematics, 343(2019), 712-755.

PhD thesis was written in Polish (here you can download it). Its title in English is as follows On mixing interval maps.