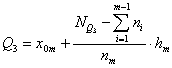Miary pozycyjne
Tomasz Bartuś
Kwantyle
Kwantyle - definiuje się jako wartości cechy badanej zbiorowości, przedstawionej w postaci szeregu statystycznego, które dzielą zbiorowość na określone części pod względem liczby jednostek, części te pozostają do siebie w określonych proporcjach.
Kwartyl pierwszy (Q1) dzieli zbiorowość na dwie części w ten sposób, że 25% jednostek zbiorowości ma wartości cechy niższe bądź równe kwartylowi pierwszemu Q1, a 75% równe bądź wyższe od tego kwartyla.
Kwartyl drugi (mediana) (Me) dzieli zbiorowość na dwie równe części; połowa jednostek ma wartości cechy mniejsze lub równe medianie, a połowa wartości cechy równe lub większe od Me; stąd nazwa wartość środkowa.
Kwartyl trzeci (Q3) dzieli zbiorowość na dwie części w ten sposób, że 75% jednostek zbiorowości ma wartości cechy niższe bądź równe kwartylowi pierwszemu Q3, a 25% równe bądź wyższe od tego kwartyla.
Decyle np. decyl pierwszy oznacza, że 10% jednostek ma wartości cechy mniejsze bądź równe od decyla pierwszego, a 90% jednostek wartości cechy równe lub większe od decyla pirwszego.
Kwartyl drugi (mediana Me)
Dla szeregu szczegółowego:
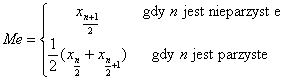
Dla szeregu rozdzielczego (graficznie lub analitycznie):
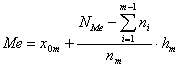
gdzie:
m - numer przedziału (klasy), w które występuje mediana,
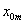 - dolna granica przedziału, w którym występuje mediana
- dolna granica przedziału, w którym występuje mediana
nm - liczebność przedziału mediany, tzn. klasy o numerze m,
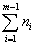 - suma liczebności przedziałów poprzedzających przedział mediany, czyli liczebność skumulowana,
- suma liczebności przedziałów poprzedzających przedział mediany, czyli liczebność skumulowana,
hm - rozpiętość przedziału klasowego, w którym jest mediana,
NMe - pozycja mediany, czyli:
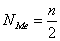
Kwartyl pierwszy Q1 i trzeci Q3
Dla szeregu szczegółowego kwartyl pierwszy i trzeci wyznacza się w ten sposób, że w dwóch częściach zbiorowości, które powstały po wyznaczeniu mediany, ponownie wyznacza się medianę; mediana w pierwszej części odpowiada kwartylowi pierwszemu, a w drugiej kwartylowi trzeciemu.
Dla szeregu rozdzielczego wyznaczenie kwartyli poprzedza się ustaleniem ich pozycji:
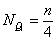
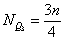
Kwartyl pierwszy Q1
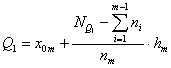 Kwartyl trzeci Q3
Kwartyl trzeci Q3
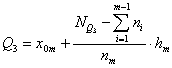
gdzie:
m - numer przedziału (klasy), w którym występuje odpowiadający mu kwartyl,
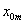 - dolna granica tego przedziału,
- dolna granica tego przedziału,
nm - liczebność przedziału, w którym występuje odpowiedni kwartyl,
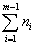 - liczebność skumulowana do przedziału poprzedzającego kwartyl,
- liczebność skumulowana do przedziału poprzedzającego kwartyl,
hm - rozpiętość przedziału klasowego, w którym jest odpowiedni kwartyl.
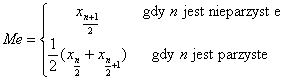
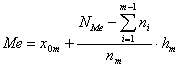
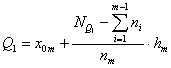 Kwartyl trzeci Q3
Kwartyl trzeci Q3