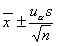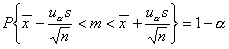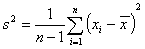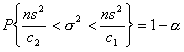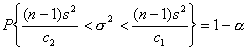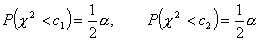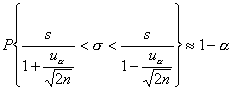Estymacja przedziałowa
Tomasz Bartuś
Estymacja przedziałowa polega na konstrukcji przedziału liczbowego, który z określonym z góry prawdopodobieństwem (najczęściej bliskim jedności), będzie zawierał nieznaną, prawdziwą wartość szacowanego parametru z populacji generalnej. Poszukiwany przedział jest nazywany przedziałem ufności (np. przedział ufności dla średniej arytmetycznej, przedział ufności dla wariancji itd.). Prawdopodobieństwo z którym chcemy poznać prawdziwe położenie wybranych parametrów statystycznych nazywane jest współczynnikiem ufności. Zaznacza się je najczęściej jako (1 - α) i określa jako 100 ⋅ (1 - α) - procentowy przedział ufności.
Samo α (poziom istotności) wyraża prawdopodobieństwo popełnienia błędu I-go rodzaju (Tab. 1). Określa maksymalne ryzyko błędu jakie jesteśmy skłonni zaakceptować. Wybór jego wartości zależy od badacza, natury problemu i od tego jak dokładnie chce on weryfikować swoje hipotezy, najczęściej przyjmuje się arbitralnie α = 0,05; 0,03 lub 0,01 (stąd wartości współczynnika ufności (1 - α) są najczęściej równe: 0,95; 0,97 lub 0,99).
Tab.1. Rodzaje błędów występujących podczas weryfikacji hipotez statystycznych
| Stan faktyczny (nieznany) |
Decyzja podjęta w wyniku próby |
| przyjęcie H0 (odrzucenie H1) |
odrzucenie H0 (przyjęcie H1) |
| H0 prawdziwa (H1 fałszywa) |
decyzja prawidłowa |
błąd pierwszego rodzaju |
| H0 fałszywa (H1 prawdziwa) |
błąd drugiego rodzaju |
decyzja prawidłowa |
Przedziały ufności poszczególnych parametrów populacji wyznacza się z rozkładów odpowiednich statystyk, będących estymatorami tych parametrów (Greń, 1976).
Wyznaczenie przedziału ufności dla średniej
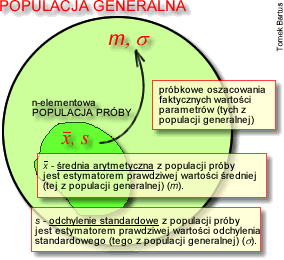
W związku z tym, że średnia wartość badanej cechy stanowi najczęściej szacowany parametr populacji generalnych, szczególne znaczenie ma znajomość przedziału ufności dla tego właśnie parametru. Najbardziej popularnym estymatorem wartości przeciętnej w populacji generalnej (m) jest średnia arytmetyczna (x̄) z próby. Ma ona wszelkie porządane cechy estymatorów: zgodność, nieobciążoność, efektywność i dostateczność. Jej rozkład wykorzystuje się do budowy przedziału ufności dla wartości średniej w populacji. W zależności od przyjętych założeń otrzymuje się konkretne wzory na przedziały ufności. W naszym przypadku założymy, że populacja generalna ma rozkład normalny (N(m, σ)). Przedział ufności dla wartości średniej dany jest wówczas wzorem:
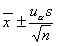
gdzie:
x̄ - średnia arytmetyczna obliczona na podstawie n - elementowej populacji próby,
s - próbkowe oszacowanie odchylenia standardowego,
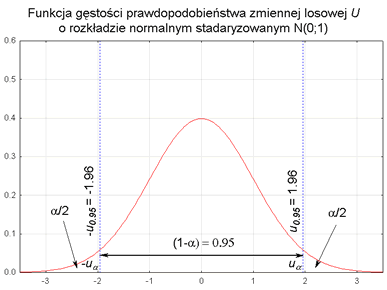
uα wartość zmiennej losowej U o sdandaryzowanym rozkładzie normalnym (N(0, 1)) wyznaczona w taki sposób aby spełniona była relacja:
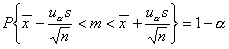
Warto zapamiętać, że dla:
1 - α = 0,95; uα = 1,96;
1 - α = 0,99; uα = 2,58;
Wyznaczenie przedziału ufności dla wariancji
W badaniach statystycznych, do najcząściej szacowanych parametrów, obok średniej arytmetycznej należy wariancja (σ2) (lub odchylenie standardowe (σ)) badanej cechy. Gdy rozkład badanej cechy jest normalny (lub zbliżony do normalnego), można zbudować przedział ufności dla wariancji. Tak jak zwykle, przedział ufności dla wariancji, opiera się na rozkładzie statystyki będącej jej estymatorem. Najbardziej znanymi estymatorami wariancji w populacji generalnej są statystyki:
a)
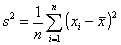
b)
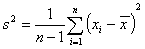
Wprawdzie estymator wariancji ze wzoru (b) jest nieobciążonym estymatorem wariacji (σ2), podczas gdy estymator ze wzoru (a) jest obciążonym estymatorem wariacji (σ2) (zob.: Obciążenie estymatora wariancji), ale oba te estymatory są równoważne jeżeli chodzi o przedział ufności dla wariancji. Natomiast oba estymatory odchylenia standardowego (obliczone jako pierwiastki kwadratowe wariancji ze wzorów (a) i (b)) są obciążonymi estymatorami odchylenia standardowego (σ).
W zależności od liczebności próby, przedział ufności budujemy w oparciu o rozkład statystyki s2 (tzn. rozkład χ2), bądź też o jej rozkład graniczny (rozkład normalny).
Obliczając pierwiastki kwadratowe z krańcowych elementów przedziału ufności dla wariancji (σ2), otrzymamy przedział ufności dla odchylenia standardowego (σ).
W zależności od liczebniości próby mamy dwa sposoby obliczania przedziałów ufności dla odchylenia standardowego (σ).
MODEL I (dla małej liczebności próby)
Gdy rozkład badanej cechy w populacji generalnej jest normalny o parametrach: m i σ oraz liczebność populacji próby jest mniejsza niż 30 elementów (n < 30), obliczamy ze wzoru (a) lub (b) próbkowe oszacowanie wariancji.
gdy wariancję liczono ze wzoru (a):
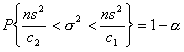
gdy wariancję liczono ze wzoru (b):
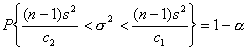
gdzie:
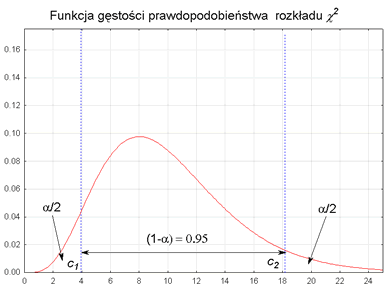
c1, c2 - są wartościami zmiennej χ2 wyznaczone z tablicy rozkładu χ2 dla n - 1 stopni swobody oraz współczynnika ufności (1 - α) w taki sposób aby spełnione były relacje:
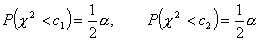
W związku z tym, że powszechnie używane tablice rozkładu χ2 podają wartości krytyczne statystyki χ2, zatem dla określonego współczynnika ufności (1 - α), wartość c2 znajdujemy w tablicach dla prawdopodobieństwa: 1 - (½) α, natomiast wartość c1 dla prawdopodobieństwa: (½) α
MODEL II (dla dużej liczebności próby)
W przypadku, gdy mamy do czynienia z liczną populacją próby i rozkład badanej cechy nie podważa zgodności rozkładu cechy w populacji generalnej z rozkładem normalnym (N(m, σ)), obliczamy z próby oszacowania odchylenia standardowego (s). Wtedy przedział ufności dla odchylenia standardowego (σ) w populacji generalnej jest określony wzorem:
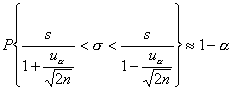
gdzie:
s - próbkowe oszacowanie odchylenia standardowego,
uα - wartość zmiennej losowej U o sdandaryzowanym rozkładzie normalnym (N(0, 1)) wyznaczoną w taki sam sposób jak dla średniej arytmetycznej.