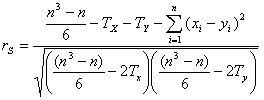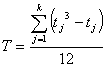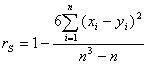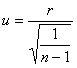Korelacja rang
Tomasz Bartuś
[na podstawie: Krawczyk, Słomka, 1982]
Analiza rang jest narzędziem przy opisie danych półilościowych (porządkowych) oraz przydatna jest do oceny związków korelacyjnych pomiędzy cechami, z których jedna ma charakter ilościowy, a druga - porządkowy. Wartym zaznaczenia jest fakt, że w tym przypadku, w przeciwieństwie do zwykłej analizy korelacji, od cech ilościowych nie wymaga się normalności rozkładu. Część materiałów dotycząca analizy danych półilościowych będzie ograniczona do analizy korelacji. Na wstępie należy jednak odpowiednio przetworzyć dane.
Przygotowanie danych
Przetworzenie danych polega na nadaniu poszczególnym elementom badanej próby numerów porządkowych, zwanych dalej rangami. Podstawą procesu rangowania są wartości cech, których związek chcemy oszacować. W zależności od charakteru danych pierwotnych rangowanie przebiegać będzie w nieco odmienny sposób.
ZASADY PODSTAWOWE
Gdy cecha, która ma zostać poddana rangowaniu jest półilościowa, rangowanie polega wyłącznie na uporządkowaniu elementów wg. rosnących (lub malejących) wartości tej cechy. W następnym kroku tak utworzonemu ciągowi nadaje się rangi przyporządkowując kolejnym elementom próby wartości kolejnych liczb całkowitych (rozpoczynając od 1). W ten sposób pierwszemu elementowi próby (ciągu) przyporządkowuje się 1, kolejnemu 2, następnemu 3 itd. Przyporządkowane numery są rangami ze względu na rozpatrywaną cechę.
Gdy badana cecha ma charakter ilościowy, rangowanie, podobnie jak poprzednio, polega na uporządkowaniu danych od najmniejszych wartości do największych (lub odwrotnie). rangami będą wtedy numery porządkowe kolejnych wyrazów utworzonego w ten sposób ciągu.
Rangi połączone
W przypadku gdy kolejne elementy próby (po uporządkowaniu danych) charakteryzują się dokładnie takimi samymi wartościami rangowanej cechy, nadaje się im tzw. rangi połączone. Rangi połączone obliczane są jako średnia arytmetyczna rang, jakie otrzymałyby te elementy, gdyby zajmowały w utworzonym ciągu nie to samo miejsce, ale miejsca sąsiednie. W związku z tym rangi połączone nie muszą mieć wartości całkowitych.
Mamy dane:
| i |
cecha X (ilościowa) |
cecha Y (półilościowa) |
| 1 |
5,32 |
2 |
| 2 |
1,7 |
3 |
| 3 |
2,1 |
1 |
| 4 |
7,5 |
2 |
| 5 |
1,7 |
2 |
| 6 |
2,1 |
3 |
| 7 |
2,1 |
4 |
| 8 |
1,0 |
2 |
Chcąc obliczyć rangi, szeregujemy cechy (każdą osobno) od najmniejszej do największej:
| lp |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| xi |
1,0 |
1,7 |
1,7 |
2,1 |
2,1 |
2,1 |
5,32 |
7,5 |
| rangi xi |
1 |
(2 + 3) / 2 = 2,5 |
2,5 |
(4 + 5 + 6) / 3 = 5 |
5 |
5 |
7 |
8 |
| yi |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
4 |
| rangi yi |
1 |
3,5 |
3,5 |
3,5 |
3,5 |
6,5 |
6,5 |
8 |
Ostatecznie otrzymujemy:
| i |
cecha X |
cecha Y |
rangi |
| xi |
yi |
| 1 |
5,32 |
2 |
7 |
3,5 |
| 2 |
1,7 |
3 |
2,5 |
6,5 |
| 3 |
2,1 |
1 |
5 |
1 |
| 4 |
7,5 |
2 |
8 |
3,5 |
| 5 |
1,7 |
2 |
2,5 |
3,5 |
| 6 |
2,1 |
3 |
5 |
6,5 |
| 7 |
2,1 |
4 |
5 |
8 |
| 8 |
1,0 |
2 |
1 |
3,5 |
Współczynnik korelacji rangowej Spearmana
Współczynnik korelacji rangowej Spearmana liczy się wg. wzoru:
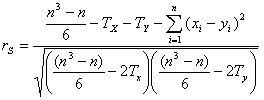
gdzie:
n - liczebność próby,
xi, yi - rangi i - tego elementu według pierwszej i drugiej cechy,
Tx, Ty - poprawki na połączenia rang, dane wyrażeniem), indeksy "x" i "y" służą wyłącznie do rozróżnienia cech.
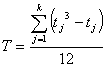
gdzie:
tj - ilość rang łączonych przy j - tym połączeniu,
k - ilość połączeń.
Gdy: Tx=Ty=0 (brak połączeń rang), współczynnik korelacji rangowej Spearmana można obliczać ze wzoru:
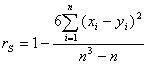
Obliczmy współczynniki Tx i Ty:
Tx = [(23 - 2) + (33 - 3)] / 12 =
Ty = [(43 - 4) + (23 - 2)] / 12 =
Istotność współczynnika Spearmana
Stawiamy hipotezę zerową w brzmieniu: H0: rS = 0
Ocena istotności współczynnika Spearmana odbywa się różnie w zależności od liczebności badanej próby.
- dla prób mało licznych - musimy korzystać ze specjalnych tablic,
- dla prób zawierających więcej niż 10 składników - posługujemy się przybliżeniami, które uniezależniają nas od tablic statystycznych.
Jeżeli współczynnik rS został obliczony z conajmniej kilkunastu elementów, to zmienna losowa:
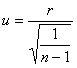
ma standaryzowany rozkład normalny N(0, 1). Wystarczy zatem obliczyć wartość u dla badanej próby i porównać ją z wartością krytyczną uα, która dla odpowiednich poziomów istotności wynosi:
- dla α = 0,1; u0,1 = 1,64,
- dla α = 0,05; u0,05 = 1,96,
- dla α = 0,01; u0,01 = 2,58.
gdy:
|u| ≥ uα - H0 odrzucamy;
|u| < uα - nie ma podstaw do odrzucenia H0.