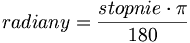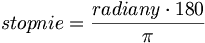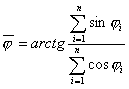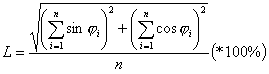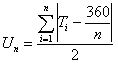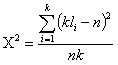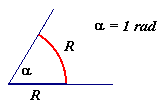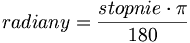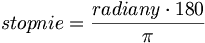Analiza danych kierunkowych
Tomasz Bartuś
na podstawie: (Krawczyk, Słomka, 1982)
Dane kierunkowe są przedstawiane w postaci wektorów (najczęściej wartości kątowych). Ten szczególny rodzaj danych ma głębokie zastosowanie w naukach przyrodniczych, a w szczególności w naukach o Ziemi. W analizach GIS, na podstawie pomiarów meteorologicznych, jesteśmy często zmuszeni określić średni kierunek wiatru wiejącego na danym obszarze. W sedymentologii, na podstawie pomierzonych zwrotów hieroglifów prądowych, chcemy znać rozkład kierunków paleotransportu w basenach sedymentacyjnych. We wszystkich tego typu przypadkach stosujemy procedury analizy danych kierunkowych.
Tak jak szereg rozdzielczy, a w praktyce, najczęściej histogram, służy do opisu populacji danych skalarnych, tak w przypadku danych wektorowych do opisu populacji służy szereg rozdzielczy lub najczęściej wykres rozetowy (diagram róża). Podobnie jak histogram, tak i te wykresy przedstawia się dla liczebności lub częstości wyrażonej procentem udziału danego kierunku w całej populacji próby.
Wyznaczanie kierunku średniego
Kierunek średni jest odpowiednikiem średniej arytmetycznej dla danych skalarnych. Należy zwrócić uwagę, że średni kierunek ma swój sens w przypadku rozkładów jednomodalnych. W przypadku rozkładów wielomodalnych, najlepszym rozwiązaniem jest podział populacji próby na jednomodalne podpopulacje i określenie dla każdej osobnego kierunku średniego. Oblicza się go ze wzoru:
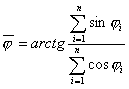
gdzie:
φ - element populacji próbny,
n - liczebność zbioru danych.
Wyznaczanie współczynnika koncentracji
Współczynnik koncentracji jest miarą rozrzutu wektorów danych od kierunku średniego. Im wyższa wartość współczynnika, tym wyższa koncentracja wartości cech wokół kierunku średniego. Oblicza się go ze wzoru zamieszczonego poniżej. W praktyce wartość współczynnika koncentracji mnożona jest przez 100% i interpretowana jako procent populacji próby skumulowana wokół kierunku średniego.
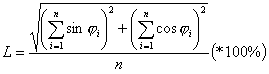
Istotność kierunku średniego
Badamy czy poszczególne dane są wystarczająco skupione wokół kierunku średniego, by można było mówić o jego istnieniu w populacji generalnej. Hipoteza zerowa głosi, że wektory próbkowe są zorientowane losowo w różnych kierunkach.
H0: L = 0;
Odrzucenie hipotezy zerowej, na przyjętym poziomie istotności (α), jest równoznaczne z przyjęciem kierunku średniego.
Test dla małych prób
Gdy dysponujemy niewielką liczbą danych pomiarowych, należy zastosować test zaproponowany przez J.S. Rao. Na wstępie należy uporządkować dane pomiarowe (φi) od wartości najmniejszej do największej. W kolejnym kroku procedury obliczamy:
Ti = φi+1 - φi
dla i = 1,2,..., n-1; oraz:
Tn = φ1 - φn+ 360
Do weryfikacji hipotezy zerowej służy statystyka:
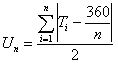
wartości krytyczne statystyki przedstawia Tab.1
Tab.1. wartości krytyczne statystyki U
| n |
α |
| 0.1 |
0.05 |
0.01 |
| 2 |
162.00 |
171.00 |
178.20 |
| 3 |
174.24 |
193.68 |
219.24 |
| 4 |
171.72 |
186.48 |
221.04 |
| 5 |
168.84 |
183.60 |
212.04 |
| 6 |
166.32 |
180.72 |
206.04 |
| 7 |
164.88 |
177.84 |
202.68 |
| 8 |
163.44 |
175.68 |
198.36 |
| 9 |
162.36 |
173.52 |
195.12 |
| 10 |
161.28 |
172.08 |
192.24 |
| 11 |
160.20 |
170.28 |
189.72 |
| 12 |
159.48 |
169.20 |
187.56 |
| 13 |
158.40 |
167.76 |
185.76 |
| 14 |
157.68 |
166.68 |
183.96 |
| 15 |
156.96 |
165.60 |
182.16 |
| 16 |
156.60 |
164.88 |
180.72 |
| 17 |
155.88 |
164.16 |
179.64 |
| 18 |
155.16 |
163.08 |
178.20 |
| 19 |
154.80 |
162.36 |
177.12 |
| 20 |
154.44 |
161.64 |
176.04 |
| źródło: Rao J.S., Sengupta S.: Mathematical Techniques for Paleocurrent Analysis: Treatment of Directional Data. Journ. Int. Assoc. Math. Geol., vol. 4, no 3, str.: 235-248. |
Jeżeli obliczona wartość statystyki przekracza wartość krytyczną (dla danego poziomu istotności), H0 należy odrzucić.
Test dla dużych prób
Gdy dysponujemy znaczną ilością danych (min. kilkadziesiąt elementów), do weryfikacji hipotezy zerowej o losowym orientacji wektorów, możemy użyć testu χ2. Należy zbudować szereg rozdzielczy, a następnie obliczyć wartość statystyki:
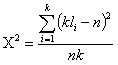
gdzie:
k - ilość klas szeregu rozdzielczego,
li - liczebność i-tej klasy,
n - liczba elementów próby.
W warunkach słuszności hipotezy zerowej, statystyka χ2 ma rozkład χ2 z k-1 stopniami swobody.
Wykonując niezbędne obliczenia w arkuszu kalkulacyjnym MS Excell, należy pamiętać, że funkcje tego programu takie jak SIN, COS, ATAN itp. wykorzystują w obliczeniach zapis kątowy wyrażony w radianach pi. Chcąc używać zapisu w stopniach, ZAWSZE, przy pomocy odpowiednich funkcji, należy radiany przeliczyć na stopnie. Więcej informacji można znaleźć w helpie do MS Excell, po naciśnięciu klawisza F1 i wpisaniu do wyszukiwarki odpowiedniej funkcji (np.: sin).
Radian (rad) jest jednostką uzupełniająca układu SI. Jest to kąt płaski równy kątowi między dwoma promieniami koła, wycinającymi z okręgu tego koła łuk o długości równej promieniowi.
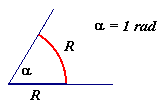
1 rad = 180o/Π = ok. 57.29578o
Wzory przeliczeniowe: