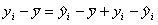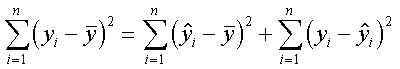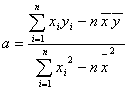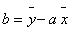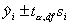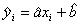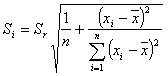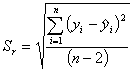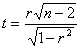Analiza regresji i korelacji dwóch zmiennych
Tomasz Bartuś
na podstawie:
Greń, 1976;
Krawczyk, Słomka, 1982;
Swan, Sandilands, 1995.
Niezwykle często w praktyce geologicznej spotykamy się z koniecznością zbadania zmienności przestrzennej jakiegoś parametru geologicznego. Dokumentacja geologiczna jak i bieżące potrzeby podmiotów eksploatujących zasoby geologiczne wymagają gromadzenia danych na temat szeregu różnych parametrów kopaliny. Badania tego typu są zawsze bardzo kosztowne. W celu przynajmniej częściowego ograniczenia tych kosztów stosowana jest często analiza regresji i korelacji. Analiza korelacyjna korzystająca z modelu korelacyjnego pozwala oceniać wartości oczekiwane jednej zmiennej losowej na podstawie pojedynczych reprezentacji innej zmiennej losowej (skorelowanej z pierwszą zmienną). Należy przy tym pamiętać, że skorelowanie to powinno mieć charakter przyczynowo - skutkowy. Czasami można obserwować pozorną zależność między badanymi cechami np. pomiędzy wzrostem ludzi, a IQ (IQ zależy w pewnym stopniu od długości życia ale nie od wzrostu). Badanie współzależności cech nosi nazwę analizy regresji i korelacji.
Cytując (Greń, 1976) Analiza korelacji i regresji jest działem statystyki zajmującym się badaniem związków i zależności pomiędzy rozkładami dwu lub więcej badanych cech w populacji generalnej. Termin regresja dotyczy kształtu zależności pomiędzy cechami. Dzieli się na analizę regresji liniowej i nieliniowej. W przypadku analizy nieliniowej, graficzną reprezentacją współzależności są krzywe wyższego rzędu np. parabola. Pojęcie korelacji dotyczy siły badanej współzależności. Analiza regresji i korelacji może dotyczyć dwóch i większej ilości zmiennych (analiza wieloraka). W tym miejscu zajmować się będziemy jedynie najprostszym przypadkiem regresji prostoliniowej dwóch zmiennych.
Korelacja dwóch zmiennych.
Najważniejszym miernikiem siły związku prostoliniowego między dwiema cechami mierzalnymi jest współczynnik korelacji liniowej Pearsona lub krócej współczynnik korelacji.
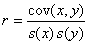
W liczniku występuje kowariancja (cov(x,y)) będąca średnią arytmetyczną iloczynu odchyleń wartości zmiennych X i Y od ich średnich arytmetycznych.
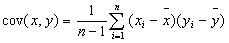
Nieintuicyjne wyrażenie (n - 1), występujące w mianowniku wzoru na kowariancję wiąże się, tak jak w przypadku wariancji z obciążeniem estymatora. Zastosowanie w mianowniku samego n, wiązałoby się z niedoszacowaniem kowariancji.
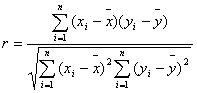
Współczynnik korelacji liniowej Pearsona mówi o sile i kierunku związku między zmiennymi. Przyjmuje wartości z przedziału [-1; 1]. Im jest bliższy "0" tym związek jest słabszy. Im bliżej "1" (lub "-1"), tym związek jest silniejszy. Wartość wspołczynnika równa "1" oznacza idealny związek liniowy (uzyskuje się go często w trakcie przypadkowej analizy korelacyjnej cechy A z cechą A).
Znak współczynnika korelacji mówi o kierunku związku: "+" oznacza związek dodatni, tj. wzrost (spadek) wartości jednej cechy powoduje wzrost (spadek) wartości drugiej (związek wprost proporcjonalny). Znak "-" oznacza kierunek ujemny, tj. wzrost (spadek) wartości cechy powoduje spadek (wzrost) wartości drugiej (związek odwrotnie proporcjonalny). Przyjmuje się następujące oceny siły związku (pamiętając o odpowiedniej liczebności próby):
Tab. 1. Opisowe określenia siły związków korelacyjnych
| r |
siła związku korelacyjnego |
| 0,0-0,2 |
brak |
| 0,2-0,4 |
słaba |
| 0,4-0,7 |
średnia |
| 0,7-0,9 |
silna |
| 0,9-1,0 |
bardzo silna |
Współczynnik determinacji
Jeżeli X będzie zmienną niezależną (objaśniejącą), a Y zmienną zależną (objaśnianą), powiązaną z X zależnością korelacyjną, to odchylenie całkowite (zob. rys. poniżej) punktu o wartości zmiennnej Y = yi od wartości średniej (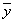 ) można przedstawić następująco:
) można przedstawić następująco:
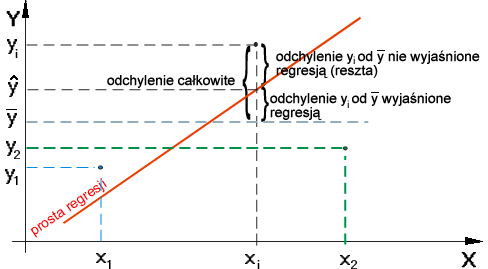
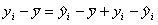
W analogiczny sposób, podnosząc do kwadratu obie strony równości i sumując po i = 1, 2,..., n, całkowitą zmienność wszystkich wartości yi możemy określić jako sumę kwadratów. Podniesienie do kwadratu jest konieczne ponieważ część wartości Y = yi odchyla się od wartości średniej "in plus", a część "in minus". Tak więc dostaniemy:
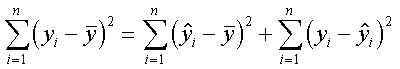
Równość ta wyraża podział całkowitej sumy kwadratów odchyleń dla zmiennej y na dwa składniki:
- sumę kwadratów odchyleń wyjaśnioną efektem regresji (EFEKT),
- resztową sumę kwadratów odchyleń (nie wyjaśnioną regresją) (RESZA).
Dla uproszczenia zapisu równanie powyższe często jest przedstawiane w postaci:
SST = SSR + SSE
gdzie:
SST - zmienność całkowita zmiennej zależnej (całkowita suma kwadratów - ang.: Total Sum of Squares),
SSR - część zmienności wyjaśniona modelem regresji (suma kwadratów odchyleń regresyjnych - ang.: Sum of Squares due to Regression),
SSE - zmienność przypadkowa (losowa) - suma odchyleń wartości yi od prostej regresji (resztowa suma kwadratów odchyleń / suma kwadratów błędów - ang.: Sum of Squares due to Error).
Przyjrzyjmy się teraz, jak sumy kwadratów mogą być wykorzystane jako miary jakości dopasowania danych do prostej regresji (modelu).
Zauważmy, że z najlepszym dopasowaniem modelu do danych, będziemy mieli do czynienia wtedy, jeżeli każda obserwacja znajdzie się dokładnie na prostej regresji (linia najmniejszych kwadratów). W tym przypadku, prosta regresji będzie przechodziła, przez każdy punkt wyznaczony parami wartości zmiennych losowych X i Y. Nie będzie żadnych błędów więc SSE = 0. Jeżeli tak, to przy idealnym dopasowaniu modelu, SSR musi być równe SST, a więc stosunek:
SSR / SST = 1
W przeciwnej sytuacji, gorsze dopasowanie modelu do danych spowoduje wzrost wartości błędów czyli SSE. Ponieważ:
SST = SSR + SSE
Z maksymalnym SSE (i najgorszym dopasowaniem modelu do danych) mamy do czynienia gdy SSR = 0. W ten sposób, najgorsze z możliwych dopasowanie daje stosunek:
SSR / SST = 0
Zdefiniujmy więc miarę dopasowania modelu do danych r2 jako współczynnik determinacji (ang.: coefficient of determination):
r2 = SSR / SST
Zauważmy: Wartości współczynnika determinacji zawsze zmieniają się w przedziale pomiędzy "0" a "1". Jest on opisową miarą użyteczności modelu równania regresji. Wartości r2 w pobliżu zera wskazują, że model nie jest przydatny do predykcji wartości zmiennej zależnej Y za pomocą zmiennej niezależnej X, natomiast wartości r2 zbliżone do "1" wskazują, że równanie regresji jest bardzo przydatne do przewidywania wartości zmiennej zależnej Y za pomocą zmiennej niezależnej X.
Wartości r2 mnoży się najczęściej razy 100% i interpretuje, jako procentowy udział całkowitej zmienności zmiennej zależnej Y, który został wytłumaczony zmiennością zmiennej objaśniejącej (niezależnej) X (SSR / SST).
Współczynnik determinacji jest opisową miarą dopasowania modelu regresji do danych, czyli miarą siły liniowego związku między danymi. Mierzy on część zmienności zmiennej objaśnianej Y, która została wyjaśniona liniowym oddziaływaniem zmiennej objaśniającej X (lub zmiennych objaśniających w analizie wielorakiej). Oblicza się go ze wzoru:
SST = SSR + SSE /: SST
1 = SSR / SST + SSE / SST
SSE / SST = 1 - SSR / SST
SSE / SST = 1 - r2
Wartości 1-r2 mnoży się najczęściej razy 100% i interpretuje, jako procentowy udział całkowitej zmienności zmiennej zależnej Y, który nie został wytłumaczony zmiennością zmiennej objaśniejącej (niezależnej)
X (SSE / SST).
Prosta regresji
Graficzną reprezentacją związku korelacyjnego jest wykres rozrzutu (diagram korelacyjny).

Na podstawie wykresu, bez obliczeń współczynnika korelacji, w przybliżony sposób możemy wnioskować o kierunku i sile związku korelacyjnego. Gdy punkty badanej korelacji grupują się wzdłuż hipotetycznej prostej (prosta regresji), przyjmując kształt zbliżony do cygara, świadczy to o znacznej sile związku. Duża ilość punktów odstających od tej prostej, przyjmujących łącznie kształt mniej lub bardziej regularnej chmury, świadczy o słabości badanego związku. Gdy wraz ze wzrostem wartości cechy niezależnej następuje wzrost wartości zmiennej zależnej mówimy o związku wprost proporcjonalnym. W przeciwnym wypadku (takim jak na wykresie powyżej), mamy do czynienia z zależnością odwrotnie proporcjonalną.
Równanie prostej regresji
Zagadnienie modelowania współzależności dwóch badanych cech realizowane jest przez obliczenie równania prostej regresji i obliczenie dla niego interesującego nas (np. 95-procentowego) przedziału ufności. Gdy wspomniane równanie jest liniowe, mówimy o regresji liniowej, w przeciwnym razie mamy do czynienia z regresją krzywoliniową.
Załóżmy, że znamy wartości zmiennej niezależnej X, natomiast wartości zmiennej zależnej Y są nieznanymi wartościami zmiennej losowej. Ich średnie wartości spełniają równanie:
Tab. 2. Równania prostych regresji dla populacji generalnej i populacji próby
| |
Dla populacji próby |
Dla populacji generalnej |
| równanie prostej regresji |
Y = aX + b |
Y = αX + β |
| współczynnik kierunkowy prostej |
a |
α |
| współczynnik przesunięcia prostej |
b |
β |
Równanie prostej regresji należy tak wymodelować, aby było najlepiej dopasowane do danych empirycznych. Współczynniki a i b są zwykle szacowane metodą najmniejszych kwadratów (MNK), która polega na takim ich doborze, aby suma kwadratów odchyleń rzędnych punktów empirycznych od wykresu prostej regresji była najmniejsza. Współczynniki prostej regresji oblicza się ze wzorów:
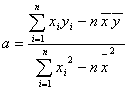
Współczynnik przesunięcia prostej regresji (b) szacuje się podstawiając próbkowe oszacowania średnich wartości w populacjach X i Y do wzoru na prostą regresji:
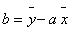
Interpretacja parametru a prostej regresji:
a > 0 jeśli "x" wzrośnie o 1 jednostkę, to "y" wzrośnie średnio o "a" jednostek.
a < 0 jeśli "x" wzrośnie o 1 jednostkę, to "y" spadnie średnio o "a" jednostek.
Obszar ufności
Oszacowanie parametrów prostej regresji należy do analizy opisowej populacji próby. My jednak z dowolnie dobranym prawdopodobieństwem, chcielibyśmy wiedzieć gdzie leży prawdziwa prosta regresji, ta z populacji generalnej. W związku z tym, że najczęściej nie jesteśmy w stanie przebadać całej populacji, możemy jedynie próbować określić obszar (przedział), w którym, z zadanym prawdopodobioeństwem znajdzie się nasza prosta.
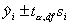
gdzie:
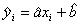
tα,df - wartość krytyczna rozkładu t-Studenta dla poziomu istotności α i liczby stopni swobody df = n - 2,
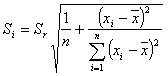
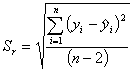
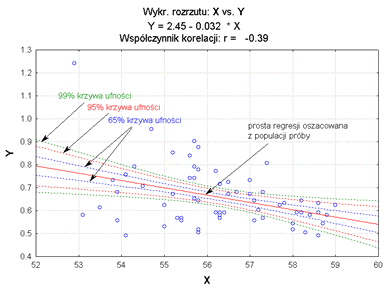
Szerokość przedziału ufności podobnie jak wariancja rośnie wraz z odchyleniem od punktu środkowego prostej regresji. Obwiednie punktów wyznaczonych przedziałami ufności dla różnych punktów xi nazywamy krzywymi ufności prostej regresji (krzywe Nevmana - krzywe wyznaczające przedziałowe prognozy wartości zmiennej Y dla danego xi). Obszar zawarty między krzywymi ufności nazywamy realizacją obszaru ufności dla prostej regresji na poziomie ufności 1 - α.
Testowanie istotności współczynnika korelacji
Ostatnim zagadnieniem, które zostanie tutaj omówione jest odpowiedź na pytanie o istotność współczynnika korelacji liniowej Pearsona. Czy w populacji generalnej zachodzi podobny związek do zaobserwowanego w populacji próby? czy też jest on jedynie dziełem przypadku. Aby to zbadać musimy założyć, że w najgorszym razie obie badane cechy mają rozkłady zbliżone do normalnych (warunek stosowalności poniższego testu). W przypadku znacznych odchyłek od tego założenia istnieje konieczność zastosowania testów nieparametrycznych.
Statystyka testowa wymaga hipotezy zerowej (H0) w brzmieniu: prawdziwa wartość współczynnika korelacji (ta z populacji generalnej) jest równa 0 (r = 0), co jest równoważne brakowi korelacji. Do weryfikacji tej hipotezy służy statystyka:
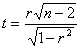
gdzie:
r - jest próbkową wartością współczynnika korelacji Pearsona,
n - liczebnością próby.
W warunkach słuszności hipotezy zerowej statystyka t ma rozkład t - Studenta z df = n - 2 stopniami swobody.
Z tablic rozkładu t- Studenta, lub kalkulatora odczytujemy dla wcześniej przyjętego poziomu istotności α - wartość krytyczną tn-2,α. Jeżeli obliczona wartość t znajduje w dwustronnym obszarze krytycznym (-∞, -tn-2, α), (tn-2,α, +∞), to H0 należy odrzucić na korzyść hipotezy alternatywnej.
gdy:
|t| ≥ tα - H0 odrzucamy;
|t| < tα - nie ma podstaw do odrzucenia H0.
Ćwiczenia:
W ramach ćwiczeń należy obliczyć współczynnik korelacji liniowej Pearsona i równania prostych regresji wszystkich badanych par zmiennych. Należy również obliczyć 95%-wy obszar ufności dla prostej regresji i przetestować istotność współczynnika korelacji. W obliczeniach (jeżeli nie są przy użyciu komputerów pomocna będzie poniższa tabela).
Tab. 3. Tabela pomocnicza do ćwiczeń
| lp |
xi |
yi |
xi - x̄ |
(xi - x̄)2 |
yi - ȳ |
(yi - ȳ)2 |
xi yi |
xi2 |
(xi - x̄)3 |
| 1 |
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
| ... |
|
|
|
|
|
|
|
|
|
| n |
|
|
|
|
|
|
|
|
|
| Σ |
... |
... |
... |
... |
|
|
... |
... |
... |
| śr. |
... |
... |
|
|
|
|
|
|
|
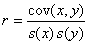
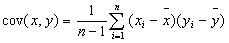
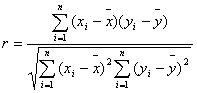
 ) można przedstawić następująco:
) można przedstawić następująco: