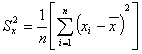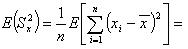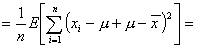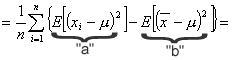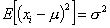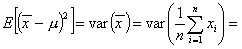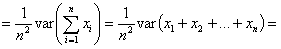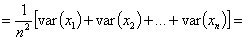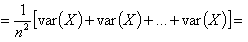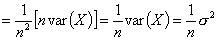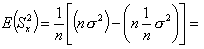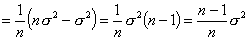Tomasz Bartuś

Obciążenie estymatora wariancji

Tomasz Bartuś

[na podstawie: Tarasiuk J., Wirtualne Wademekum Statystyki]

Przez długi czas nie mogłem zrozumieć nieintuicyjnego (n - 1) w mianowniku estymatora wariancji populacji będącej częścią zbiorowości generalnej. W przypadku estymatora średniej arytmetycznej wzór jest jasny i klarowny. Suma wszystkich wartości badanej cechy zostaje po prostu podzielona przez całkowitą liczbę obserwacji. Postaram się wytłumaczyć skąd się bierze wspomniane (n - 1) w mianowniku wariancji.

Tok rozumowania rozpoczniemy od założenia co by było gdyby estymator wariancji, tak jak w przypadku estymatora wartości średniej miał w mianowniku samo n.

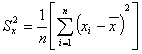
Gdzie:
S²_x - estymator wariancji populacji próby (wariancja próbkowa)
n - liczba elementów populacji próby,
x_i - i-ty element populacji próby,
x̄ - średnia z populacji próby (średnia próbkowa),

Estymator jest zmienną losową. Jeżeli policzymy wartość wariancji próbkowej (S²_x) dla wielu różnych prób, zawsze otrzymamy inną wartość estymatora.

Estymator jest nieobciążony, jeżeli wartość oczekiwana (wartość przeciętna) z estymatora (E(S²_x)) jest równa wartości estymowanego parametru (Θ). W tym przypadku należałoby zadać pytanie czy estymator wariancji (S²_x) (wariancja próbkowa) jest równy wariancji z populacji generalnej (σ²). Wszystko co trzeba teraz zrobić to sprawdzić czy tak jest w tym przypadku.

W związku z tym, że wartość oczekiwana ze stałej (tutaj = 1 / n jest równa tej stałej (własności wartości oczekiwanej)), możemy napisać:

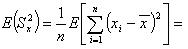
Zastosujmy trik polegający na dodaniu i odjęciu wartości średniej z populacji generalnej (μ)

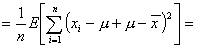
Wartość oczekiwana sumy zmiennych losowych jest równa sumie wartości oczekiwanych tych zmiennych (własności wartości oczekiwanej):

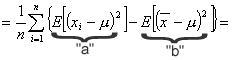
a)
Wartość oczekiwana kwadratu odchyłek zmiennej losowej X od jej wartości oczekiwanej (przeciętnej), z definicji jest równa wariancji zmiennej losowej:

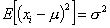
b)

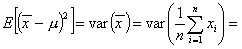
Wariancja iloczynu stałej (w tym przypadku 1 / n) i zmiennej losowej, równa się iloczynowi kwadratu tej stałej i wariancji tej zmiennej (własności wariancji zmiennej losowej):

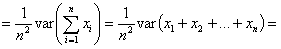
wariancja sumy zmiennych losowych jest równa sumie wariancji tych zmiennych (własności wariancji zmiennej losowej):

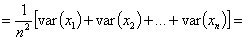
każda zmienna x_i podlega temu samemu rozkładowi. Jest to rozkład zmiennej losowej X. Tak więc wariancja każdej ze zmiennych x_i jest równa wariancji zmiennej losowej X:

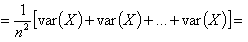
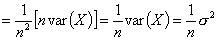
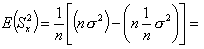
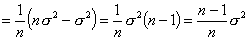
Widać więc, że wartość oczekiwana estymatora wariancji zależy od n. Estymator jest więc obciążony. Wartość oczekiwana nie może być równa wartości wyestymowanej. Jak zatem powinien wyglądać estymator nieobciążony. Oczywiście w mianowniku zamiast n powinien mieć n - 1.