Test Kołmogorowa - Smirnowa
Tomasz Bartuś
[na podstawie: Krawczyk, Słomka, 1982]
Test Kołmogorowa-Smirnowa (K-S) jest obok testu Χ2 drugim, najważniejszym testem badającym zgodność rozkładu empirycznego (próbkowego) z rozkładami teoretycznymi (w szczególności z rozkładem normalnym). W porównaniu z testem Χ2 jest obarczony wadą polegającą na braku możliwości jego zastosowania w przypadku badania populacji cechujących się rozkładami dyskretnymi (skokowymi). Niewątpliwą zaletą testu jest zaś możliwość wykorzystania go w trakcie badań rozkładów bardzo nielicznych populacji prób (odmiana testu dla prób o niewielkiej liczebności).
Test K-S wykorzystuje statystykę λ, która opiera się na porównaniu dystrybuanty empirycznej (kumulanty) ze stablicowaną dystrybuantą teoretyczną, wynikającą z weryfikowanej hipotezy zerowej H0.
Stawiamy hipotezę zerową (H0):
H0: F(xi') = K(xi') (w przypadku odmiany testu dotyczącej populacji małolicznych), lub:
H0: F(ai') = K(ai') (w przypadku odmiany testu dotyczącej populacji licznych),
W następnym kroku analizy należy wypełnić Tab. 1 lub Tab. 2.
Dla populacji małolicznych:
Tab. 1. Obliczenia dla małolicznych populacji
| i |
xi |
xi' |
K(xi') |
F(xi') |
|K(xi') - F(xi')| |
| 1 |
|
|
|
|
|
| 2 |
|
|
|
|
|
| ... |
|
|
|
|
|
| n |
|
|
|
|
|
gdzie:
i - numer kolejny próby w szeregu pozycyjnym,
xi - wartość próby z uporządkowanego rosnąco szeregu pozycyjnego,
xi' - wartość próby, które zostały zestandaryzowane do postaci rozkładu normalnego o parametrach: N(0,1) (zob. UWAGA 1)
K(xi') - dystrybuanta zestandaryzowanego rozkładu empirycznego wg. wzoru:
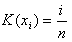
gdzie:
i - numer próby w szeregu pozycyjnym,
n - ilość elementów w całej populacji próby,
F(xi') - wartość dystrybuanty teoretycznej rozkładu N(0, 1), odczytane z tablic statystycznych (zob. UWAGA 2)
|K(xi') - F(xi')| - wartości bezwzględne różnic pomiędzy dystrybuantami empirycznymi, a teoretycznymi.
Dla populacji licznych:
Tab. 2. Obliczenia dla licznych populacji
| i |
ai |
ai' |
ni |
K(ai') |
F(ai') |
|K(ai') - F(ai')| |
| 1 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| ... |
|
|
|
|
|
|
| n |
|
|
|
|
|
|
gdzie:
i - numer kolejny klasy szeregu rozdzielczego,
ai - górne granice przedziałów klasowych szeregu rozdzielczego,
ai' - zestandaryzowane górne granice przedziałów klasowych szeregu rozdzielczego,
K(ai') - dystrybuanta zestandaryzowanego rozkładu empirycznego wg. wzoru:
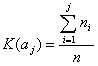
gdzie:
ni - liczebność i - tej klasy szeregu rozdzielczego,
n - ilość elementów w całej populacji próby,
F(ai') - wartość dystrybuanty teoretycznej rozkładu N(0, 1), odczytane z tablic statystycznych (zob. UWAGA 2)
|K(ai') - F(ai')| - wartości bezwzględne różnic pomiędzy dystrybuantami empirycznymi, a teoretycznymi.
W następnym kroku obliczamy statystykę:
dla zbiorów małolicznych:
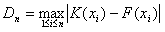
Statystyka w warunkach prawdziwości hipotezy zerowej (H0) ma znany, stablicowany rozkład. Hipotezę zerową odrzucamy, gdy obliczona wartość Dn będzie większa lub równa stablicowanej wartości krytycznej na obranym wcześniej poziomie istotności
W przypadku licznych populacji, do weryfikacji hipotezy zerowej wykorzystuje się rozkład (graniczny) statystyki λ
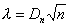
gdzie:
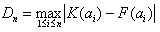
Z tablic rozkładu (granicznego) λ Kołmogorowa odczytujemy wartość krytyczną statystyki λ dla obranego poziomu istotności ( λα). Jeżeli spełniony zostaje warunek:
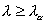
..., wtedy istnieją przesłanki do odrzucenia hipotezy zerowej (H0). Innymi słowy populacja próby nie daje podstaw do stwierdzenia, że populacja generalna charakteryzuje się rozkładem normalnym.
UWAGI
Uwaga 1: STANDARYZACJA ROZKŁADÓW DO POSTACI N(0, 1)
Chcąc porównać dowolny rozkład empiryczny z wybranym rozkładem teoretycznym musimy sięgnąć do tablic statystycznych. Są w nich stablicowane wybrane standardowe rozkłady teoretyczne (np. stadardowy rozkład normalny). Przez standardowe należy rozumieć rozkłady o znanych parametrach (wartości przeciętnej (średniej) i odchyleniu standardowym). W celu umożliwienia porównania rozkładów empirycznego z rozkładami standardowymi, należy przekształcić rozkład empiryczne o parametrach N(m, s) do postaci standardowej N(0, 1) czyli dokonać na nich standaryzacji. Dokonuje się tego przekształcając kolejno wszystkie wartości zmiennej losowej (w przypadku wersji testu dla małej ilości prób) lub granice przedziałów klasowych (w przypadku wersji testu dla znacznej ilości prób) wg. poniższego wzoru:
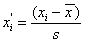
Uwaga 2: WARTOŚCI DYSTRYBUANTY DLA UJEMNYCH WARTOŚCI ZMIENNEJ LOSOWEJ X
W związku z tym, że standardowy rozkład normalny N(0, 1) jest symetryczny względem realizacji zmiennej losowej X równej wartości przeciętnej tej zmiennej (m = 0), w tablicach statystycznych przedstawia się wartości dystrybuanty teoretycznej jedynie dla nieujemnych realizacji tej zmiennej. Zgodnie z własnościami dystrybuanty, gdy zmienna losowa przyjmie wartości ujemne, ich dystrybuantę należy obliczyć wg. wzoru:
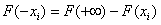
F(-xi) = 1 - F(xi)
np.: F(-2) = 1 - F(2)
.gif)
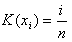
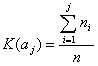
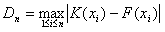
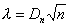
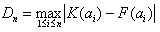
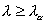
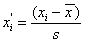
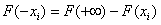
.gif)