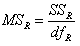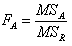Jednoczynnikowa analiza wariancji - obliczenia
Tomasz Bartuś
[na podstawie: (Krawczyk, Słomka, 1982)]
Najprostszym przypadkiem, w którym jako metodą badawczą możemy posłużyć się analizą wariancji, jest sytuacja, w której na analizowany zbiór oddziaływuje wyłącznie jeden czynnik o charakterze dyskretnym (np. miejsce opróbowania, ogniwo stratygraficzne, litologia itp.). Mówimy wtedy o jednoczynnikowej analizie wariancji, lub klasyfikacji pojedynczej.
Wyobraźmy sobie n - elementową populację próby, którą możemy podzielić ze względu na jakiś czynnik na p grup (klas). Do każdej z nich trafia pewna liczba ni: 1, 2, 3,..., j obserwacji wyczerpując całkowitą ilość obserwacji w populacji próby (n). Na rysunku umieszczonym poniżej, grupy i nazwane zostały od czterech pierwszych liter alfabetu: A, B, C i D.
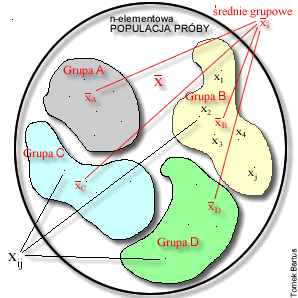
Reasumując:
ilość grup na które została podzielona populacja próby i = 1 ,2 ,..., p: p
ilość wszystkich obserwacji w populacji próby: n
ilość obserwacji znajdujących się w poszczególnych grupach: ni
średnia wartość badanej cechy w i-tej klasie: x̄i
średnia wartość czynnika w całej populacji próby: x̄
Można założyć, że j-tą próbkową wartość badanej cechy, zakwalifikowaną do i-tej klasy poziomu badanego czynnika, można zawsze przedstawić jako sumę średniej wartości badanej cechy w tej klasie i jakiejś niezależnej zmiennej losowej o rozkładzie N(0, sa), będącej po prostu losowym odchyleniem tej wartości od średniej grupowej (x̄i).
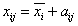
Wartość średnią badanej cechy w i-tej klasie badanego czynnika, można w ten sam sposób przedstawić jako sumę średniej obliczonej dla całej badanej populacji (średnia generalna) i zmiennej losowej będącej odzwierciedleniem odchylenia średniej grupowej od średniej generalnej.
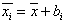
Parametr bi jest więc odzwierciedleniem oddziaływania i-tego poziomu (klasy) badanego czynnika. Łącząc powyższe dwa wzory otrzymujemy:
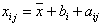
Analiza wariancji umożliwia wykorzystanie prostego spostrzeżenia. W przypadku istotnego oddziaływania badanego czynnika (np. litologii) na analizowaną cechę (np. gęstość pozorną skał), parametr bi powinien zaznaczać się silniej niż będący odzwierciedleniem zmienności wewnątrzgrupowej - aij. Na podstawie tego spostrzeżenia formułowana jest hipoteza zerowa analizy, która mówi o braku oddziaływania badanego czynnika na wartości badanej cechy.
H0: bi = 0; dla i = 1, 2,..., p
co jest równoważne z:
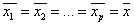
Wobec hipotezy alternatywnej, że w przynajmniej jednej z wydzielonych grup średnia istotnie odbiega od innych średnich klasowych.
W tym momencie najlepiej widać, że ANOVA jest w istocie metodą porównywania wielu średnich klasowych. W przypadku ograniczenia liczby klas do dwóch z powodzeniem może być zastąpiona testem t-Studenta równości średnich.
Punktem wyjścia do obliczeń jest spostrzeżenie, że całkowita zmienność badanej cechy (przedstawiona jako suma kwadratów odchyleń badanej cechy od wartości średniej generalnej) może być wyrażona jako suma zmienności międzygrupowej i zmienności wewnątrzgrupowych:
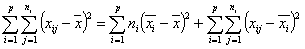
gdzie:
Dla uproszczenia zwykło się podawać wzór:
SST = SSA + SSR
w którym:
SST - miara całkowitej zmienność badanej cechy w próbie,
SSA - miara wielkość odchyleń średnich klasowych od średniej ogólnej,
SSR - miara wielkości odchyleń poszczególnych obserwacji od średnich klasowych.
SSA jest nazywany często zmiennością międzygrupową lub efektem,
SSR zmiennością wewnątrzgrupową lub błędem.
W celu zweryfikowania hipotezy zerowej o wpływie czynnika na wartości badanej cechy należy obliczyć tzw. średnie kwadraty: MSA i MSR:
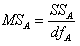 ,
,
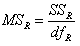
gdzie:
dfA = p - 1
dfR = n - p
W warunkach słuszności hipotezy zerowej, statystyka FA:
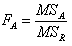
ma rozkład F - Snedecora z dfA i dfR stopniami swobody.
Aby zweryfikować hipotezę zerową należy wypełnić tzw. tabelę analizy wariancji (Tab. 1).
Tab. 1. Tabela jednoczynnikowej analizy wariancji
| źródło zmienności |
stopnie swobody |
sumy kwadratów (SS) |
średnie kwadraty (MS) |
wartość statystyki F |
| między grupami |
dfA = p - 1 |
SSA |
MSA |
F = MSA / MSR |
| wewnątrz grup (błąd) |
dfR = n - p |
SSR |
MSR |
|
Hipotezę zerową odrzucamy jeżeli obliczona wartość statystyki FA spełni nierównność:
FA ≥ Fα, dfA, dfR
gdzie:
Fα (dfA, dfR) - wartość krytyczna statystyki F dla przyjętego poziomu istotności (najczęściej 0,05) i przyjętej liczby stopni swobody (dfA, dfR).
Wartość krytyczną statystyki Fα odczytujemy z tablic statystycznych - dystrybuanty rozkładu F, lub obliczamy.
W ramach ćwiczeń należy przeprowadzić jednoczynnikową analizę wariancji. Obliczenia sprowadzają się do znalezienia: SSA, SSR i ewentualnie dla sprawdzenia SST i wypełnienia tabeli jednoczynnikowej analizy wariancji przedstawionej powyżej.
W celu przeprowadzenia niezbędnych obliczeń, dla każdej z wyłonionych kategorii (grup, klas), w arkuszu kalkulacyjnym należy sporządzić następującą tabelę:
| i-ty poziom czynnika A (i-ta klasa) |
| nr próby |
xij |
xij - x̄i |
(xij - x̄i)2 |
| P16 |
|
|
|
| P2 |
|
|
|
| P30 |
|
|
|
| ... |
|
|
|
| j |
|
|
|
| ni |
|
| x̄i |
|
| x̄ |
|
| (x̄i - x̄)2 |
|

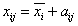
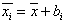
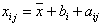
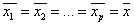
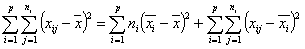
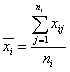
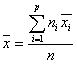
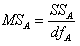 ,
,