Miary zmienności (rozproszenia, dyspersji)
Tomasz Bartuś
Tab. 1. Miary zmienności
| Miary klasyczne |
Miary pozycyjne |
wariancja
odchylenie standardowe
odchylenie przeciętne
współczynnik zmiennośc
|
rozstęp
odchylenie ćwiartkowe
współczynnik zmienności
|
Dwa rozłączne obszary badań cechowały się następującymi wartościami wskaźnika W:
Tab. 2. Pomiary wskaźnika W w obszarach A i B
| obszar |
wartość cechy |
| A |
60 |
59 |
58 |
61 |
60 |
61 |
57 |
62 |
59 |
63 |
| B |
53 |
60 |
67 |
49 |
65 |
62 |
56 |
70 |
63 |
55 |
Oba badane obszary cechują się taką samą ilością pobranych prób (ni = 10), średnie arytmetyczne wartości badanych wskaźników w obu populacjach są sobie równe i wynoszą 60. Zadajmy sobie pytanie czy poza poszczególnymi wartościami istnieje jakaś różnica pomiędzy obiema populacjami? Aby się temu lepiej przyjrzeć przedstawmy oba zbiory danych na jednej osi współrzędnych.

Szczegółowe wyniki przedstawia poniższa tabelka:
Tab. 3. Wybrane podstawowe parametry statystyczne wskaźnika "W" w obszarach A i B
| obszar |
ni |
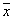 |
Me |
min |
max |
Q1 |
Q3 |
R |
| A |
10 |
60 |
60 |
57 |
63 |
59 |
61 |
6 |
| B |
10 |
60 |
61 |
49 |
70 |
55 |
65 |
21 |
Jak widać, obszar A i B wyróżniają się różnych rozrzutem danych wokół wartości średniej. W obszarze A wartość min jest znacznie wyższa niż w obszarze B, a wartość max jest znacznie niższa niż w obszarze B.
To proste spostrzeżenie pozwala na sformułowanie pierwszego, najprostszego lecz jak się okarze obarczonego znacznym mankamentem parametru statystycznego. Tym parametrem jest rozstęp (R) będący po prostu różnica pomiędzy wartościami xmax i xmin.
Rozstęp
Najprostszą i najbardziej intuicyjną miarą zmienności przypadków w populacji próby jest rozstęp. Rozstęp - różnica pomiędzy wartością maksymalną, a minimalną cechy - jest miarą charakteryzującą empiryczny obszar zmienności badanej cechy. W związku z tym, że przy jego obliczeniu ignoruje się wszystkie dane (za wyjątkiem dwóch wartości - minimalnej i maksymalnej), nie daje on jednak informacji o zróżnicowaniu poszczególnych wartości cechy w zbiorowości.
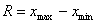
Wariancja
Tak więc rozstęp możemy uznać jedynie za wstępną miarę zmienności w populacji próby. Zresztą przyjrzyjmy się takiemu przykładowi:

Dwa obszary charakteryzują się identycznymi wartościami średnimi badanego parametru i identycznymi wartościami minimalnymi i maksymalnymi, a co za tym idzie identycznymi rozstępami. Jednak już na pierwszy rzut oka widać, że rozrzuty danych wokół wartości przeciętnej w obu przypadkach są skrajnie różne. W obszarze A dane są znacznie bardziej skumulowane przy wartości średniej niż w obszarze B.
Powyższy przykład dobitnie pokazuje konieczność istnienia parametru statystycznego opisującego całkowitą zmienność wszystkich elementów populacji próby. Parametrem tym jest wariancja.
Wariancja (s2) - jest to średnia arytmetyczna kwadratów odchyleń poszczególnych wartości cechy od średniej arytmetycznej zbiorowości.
szereg szczegółowy:
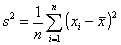
szereg rozdzielczy punktowy:
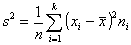
szereg rozdzielczy z przedziałami klasowymi:
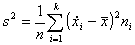
Wykonując proste przekształcenia algebraiczne, otrzymamy:
szereg szczegółowy:
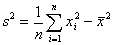
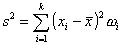
szereg rozdzielczy:
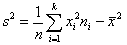
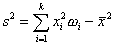
Uwaga !!! należy pamiętać o problemie obciążenia estymatora wariancji.
Gdy mamy do czynienia z opisem populacji próby (np. chcemy znać wariancję średnich prędkości samochodów, które jadąc uległy wypadkowi w woj. małopolskim w miesiącu styczniu 2022 roku (skończona liczba elementów populacji)), będziemy stosować wzory na wariancję w postaci przedstawionej powyżej. Jeżeli, jednak w obliczeniach dokonujemy estymacji wariancji występującej w jakiejś większej populacji generalnej (np.: chcemy znać wariancję średniego wzrostu Polek), zamiast ułamka 1 / n, musimy zastosować 1 / n - 1. Więcej o obciążeniu estymatora wariancji.
Odchylenie standardowe
Odchylenie standardowe (s) - jest to pierwiastek kwadratowy z wariancji. Stanowi miarę zróżnicowania o mianie zgodnym z mianem badanej cechy, określa przeciętne zróżnicowanie poszczególnych wartości cechy od średniej arytmetycznej.
Typowy obszar zmienności cechy - około 2/3 wszystkich jednostek badanej zbiorowości statystycznej posiada wartości cechy w tym przedziale:
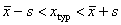
Odchylenie przeciętne
Odchylenie przeciętne (d) - jest to średnia arytmetyczna bezwzględnych odchyleń wartości cechy od średniej arytmetycznej. Określa o ile jednostki danej zbiorowości różnią się średnio, ze względu na wartość cechy, od średniej arytmetycznej.
szereg szczegółowy:
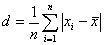
szereg rozdzielczy:
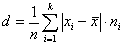
Pomiędzy odchyleniem przeciętnym i standardowym, dla tego samego szeregu, zachodzi relacja: d < s.
Odchylenie ćwiartkowe
Odchylenie ćwiartkowe (D) - jest to parametr określający odchylenie wartości cechy od mediany. Mierzy poziom zróżnicowania tylko części jednostek; po odrzuceniu 25% jednostek o wartościach najmniejszych i 25% jednostek o wartościach największych.
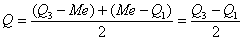
Typowy obszar zmienności cechy:
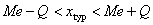
Współczynnik zmienności
Współczynnik zmienności - jest ilorazem bezwzględnej mary zmienności cechy i średniej wartości tej cechy, jest wielkością niemianowaną, najczęściej podawaną w procentach.
Klasyczne współczynniki zmienności:
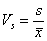 oraz
oraz
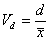
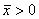
Pozycyjne współczynniki zmienności:
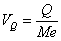
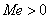
oraz
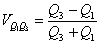
Współczynnik zmienności stosuje się w porównaniach zróżnicowania:
- kilku zbiorowości pod względem tej samej cechy,
- tej samej zbiorowości pod względem kilku różnych cech.
Tab. 4. Klasyfikacja zmienności złóż (wg. Baryszewa (Smirnow, Prokofiew, 1960)) (Mucha, 1994)
| Grupa zmienności złóż |
Zmienność |
V [%] |
| I |
mała |
0-20 |
| II |
przeciętna |
20-40 |
| III |
duża |
40-100 |
| IV |
bardzo duża |
100-150 |
| V |
skrajnie duża |
>150 |
O zmienności całego złoża zawsze decydują cechy najbardziej zmiennego parametru.