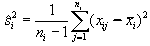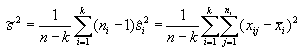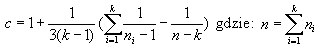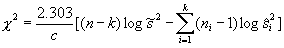Tomasz Bartuś

Testowanie założeń ANOVA

Tomasz Bartuś

UWAGA!!! materialy w tworzeniu

Zakłada się, że wariancje w obrębie wydzielonych grup układu są sobie równe; założenie to określa się mianem założenia jednorodności wariancji. Wariancję błędu (wewnątrzgrupową) oblicza się jako sumę kwadratów w obrębie grupy. W przypadku kiedy wariancje w dwóch grupach różnią się między sobą, wówczas ich dodawanie nie jest właściwe i nie daje oszacowania wspólnej wariancji wewnątrzgrupowej (ponieważ nie istnieje wspólna wariancja) (Statistica PL, 1997 str. 1703). Niespelnienie tego zalozenia moze prowadzic do zawyzania wartosci testu F i do zbyt wielu odrzucen H₀. Weryfikacji założenia dokonuje się z wykorzystaniem następujących testów:

Test Bartletta

Dotyczy on populacji normalnych, dla których chcemy sprawdzić hipotezę o równości wariancji we wszystkich podpopulacjach. Test ten oparty jest na pewnej statystyce, która ma rozkład asymptotyczny Χ². Zbieżność do rozkładu Χ² jest przy tym bardzo szybka, tak, że można go stosować nawet dla bardzo małych prób. W literaturze jest znanych kilka postaci wzoru na statystykę Bartletta. Aby uniknąć kłopotów z logarytmami naturalnymi, zostanie przytoczona postać wzoru z wykorzystaniem tylko logarytmów dziesiętnych - stąd stała występująca w tym wzorze 2,303 (jest to ln 10). Ze względu na dużą liczbę pracochłonnych rachunków testów dokonuje się jedynie przy użyciu komputerów (Greń J., 1976).

Jeżeli zalożymy, że mamy k podpopulacji o rozkładach normalnych losujemy niezależnie do próby n elementów. Mamy więc k losowych prób o liczebnościach n. Wyniki każdej próby oznaczamy symbolem x_ij (i = 1, 2, ..., k; j = 1, 2,..., n_i), a średnie x_{i śr}.

Chcemy sprawdzić hipotezę o jednorodności wariancji we wszystkich podpopulacjach.
H₀: σ²₁ = σ²₂ =... = σ²_k
H₁: nie wszystkie σ²_i są jednakowe

Z wyników k prób o liczebnościach n_i oblicza się według kolejnych wzorów:

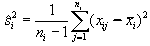
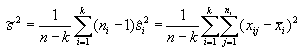
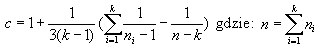
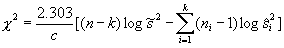
symbole logarytmów oznaczają logarytmy dziesiętne.

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ rozkład asymptotyczny Χ² z k - 1 stopniami swobody. Z tablicy rozkładu Χ², dla ustalonego z góry poziomu istotności α; i dla k - 1 stopni swobody, odczytujemy wartość krytyczną Χ²_α.

Reguła decyzyjna: Ilekroć z porównania obliczonej wartości σ² z wartością krytyczną σ²_α otrzymamy nierówność:

Χ² ≥ Χ²_α

podejmujemy decyzję odrzucenia sprawdzanej H₀.

Gdy natomiast:

Χ² < Χ²_α

nie ma podstaw do odrzucenia H₀.

Test Cochrana

Test Hartleya (test F_max)

Jeśli założymy, że każda populacja ma rozkład normalny i że ich wariancje są równe
σ²_i (i = 1, 2, ..., k),

to możemy zweryfikować hipotezy H₀: σ²₁ = σ²₂ = .... = σ²_k
H₁: nie wszystkie σ²_i są jednakowe

Reguła decyzyjna: odrzucamy H₀, jeżeli:

 
F_{max(α){kvi(max)}} odczytujemy ze specjalnej tablicy, gdzie:
k - liczba czynników;
df_i(max) - największa liczba stopni swobody spośród próbek;

F_{obl. max} = σ²_max / σ²_min

Test Levene'a

• mocny test;
• dla każdej zmiennej zależnej przeprowadzana jest ANOVA na podstawie bezwzględnych odchyleń wartości od średnich grupowych;
• jeżeli test Levene'a okaże się istotny to H₀ o jednorodności wariancji w grupach należy odrzucić.

ale F jest mocną statystyką gdy:

1. liczebności w grupach są >10 (i w przypadku równych n);
2. średnie w grupach nie są skorelowane z odchyleniami standardowymi w tych grupach;

Test jednorodności wariancji nie podważa ANOVA. Test Levene'a nie jest odporny na nierówne ilości elementó w grupach.
(STATSOFT 1516, 1521).

Test Browna - Forsythe'a

• test podobny do Levene'a;
• jest bardziej odporny na odchylenia od normalności zmiennych zależnych w grupach;
• można go stosować przy różnych liczebnościach elementów w grupach;
• zamiast wykonywać ANOVA na odchyleniach od średniej, można to samo robić na odchyleniach od median grupowych;
• opiera się na założeniu jednorodności wariancji (?);

(STATSOFT 1516, 1522).