Zakres analiz (zajęcia III)
Tomasz Bartuś
3.1.2 Miary zmienności
3.1.2.1 Przedział zmienności
Przedział zmienności nazywany jest także rozstępem lub zakresem zmienności. Jest to po prostu różnica pomiędzy wartościami maksymalną, a minimalną badanej cechy.
R = xmax - xmin
Szczegóły zob.: Miary zmienności
3.1.2.2 Wariancja
Najważniejszym i można by powiedzieć "pierwotnym" parametrem statystycznym spośród wszystkich miar zmienności jest wariancja. Dla naszych potrzeb wykorzystywać będziemy nieobciążony estymator wariancji w postaci:
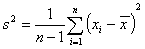
oraz oszacowanie wariancji za pomocą wzoru wykorzystującego obliczone szeregi rozdzielcze:
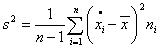
Szczegóły zob.: Miary zmienności
UWAGA: Nie zapomnieć o odpowiednich jednostkach! Wypowiedzieć się na temat oszacowań wariancji na podstawie szeregu szczegółowego i szeregu rozdzielczego. czy wartości te wyraźnie odbiegają od siebie (o ile procent), czy też są do siebie zbliżone.
3.1.2.3 Odchylenie standardowe
Odchylenia standardowe obliczamy przez spierwiastkowanie wariancji (obliczonej na podstawie nieobciążonego estymatora (wzór dla szeregu szczegółowego).
Szczegóły zob.: Miary zmienności
UWAGA: Nie zapomnieć o odpowiednich jednostkach!
3.1.2.4 Współczynnik zmienności
Współczynniki zmienności obliczamy ze wzoru:
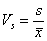
Szczegóły zob.: Miary zmienności
UWAGA: Nie zapomnieć o bezwymiarowości współczynnika zmienności! Na podstawie klasyfikacji Baryszewa podać stopień zmienności złoża ze względu na dwa badane parametry. Odpowiedzieć na pytanie, który z parametrów cechuje się relatywnie wyższym poziomem zmienności.
W ramach archiwizowania obliczeń należy sporządzić Tab.2. i ją wypełnić (kolumny 1-7).
Tab.2. Tablica obliczeń pomocniczych
| lp |
xi |
yi |
xi - x̄i |
(xi - x̄i)2 |
yi - ȳi |
(yi - ȳi)2 |
xi yi |
xi2 |
(xi - x̄i)3 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
| ... |
|
|
|
|
|
|
|
|
|
| n |
|
|
|
|
|
|
|
|
|
| Σ |
... |
... |
... |
... |
|
|
... |
... |
... |
| śr. |
... |
... |
|
|
|
|
|
|
|
UWAGA Wypełnione oraz pozostałe kolumny tabeli będą wykorzystywane w dalszych analizach m.in. do obliczenia współczynnika korelacji liniowej Pearsona.