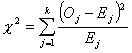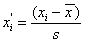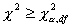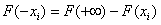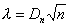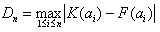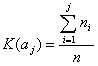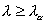Zakres analiz (zajęcia IV)
Tomasz Bartuś
2.3. Badanie zgodności rozkładów empirycznych z rozkładem normalnym za pomocą testu χ2
Badanie wykorzystuje statystykę χ2 (wzór poniżej), która bada różnice pomiędzy ilością obserwacji przypadających na kolejne klasy szeregu rozdzielczego, a teoretyczną ilością obserwacji wynikającą z weryfikacji hipotezy zerowej (np. spodziewaną ilością obserwacji w rozkładzie normalnym).
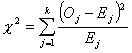
gdzie:
Oj - zdarzenia obserwowane [ang. Observed]; (w Tab. 3. wyrażone są ilością elementów próby w poszczególnych przedziałach klasowych (ni))
Ej - zdarzenia spodziewane [ang. Expected].
W jednej z wcześniejszych analiz obliczyliśmy szeregi rozdzielcze dla obu badanych zmiennych (Tab. 1.) teraz wykorzystamy je do badania zgodności rozkładów empirycznych obu zmiennych z rozkładem normalnym. W związku z tym, że nie znamy parametrów hipotetycznego rozkładu normalnego badanych prób, musimy więc skorzystać z oszacowań próbkowych.
Hipoteza zerowa (H0) głosić więc będzie, że zmienne X i Y mają rozkłady zgodne z normalnymi o parametrach: N(x̄, s).
Kolejnym krokiem powinno być obliczenie prawdopodobieństw, że nasze zmienne losowe przyjmą wartości z poszczególnych klas szeregu rozdzielczego. W związku z tym, że tablice statystyczne, w których mamy dystrybuantę rozkładu normalnego, zostały obliczone dla parametrów N(0, 1), jesteśmy zmuszeni do zestandaryzowania granic klas szeregu rozdzielczego. Standaryzacji dokonujemy wykorzystując wzór:
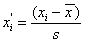
Zestandaryzowane górne granice przedziałów klasowych wpisujemy w 4 kolumnie tabeli Tab. 3 (xi max'). Dla uproszczenia przyjmiemy, że dolną granicą pierwszego przedziału klasowego jest -∞, a górną granicą ostatniego przedziału klasowego jest +∞.
Tab.3. Test χ2 normalności rozkładu zmiennej X [aa].
| lp |
xi max |
ni |
xi max' |
F(xi max') |
pi |
ei |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| ... |
|
|
|
|
|
|
| Σ |
- |
n |
- |
- |
1 |
|
Z tablicy dystrybuanty rozkładu normalnego odczytujemy wartości F(xi max'), a następnie ze związku:
pi = F(xi max') - F(xi-1 max')
obliczamy i wpisujemy do tabeli (kolumna 6) odpowiednie prawdopodobieństwa. Z poniższego wzoru możemy teraz obliczyć oczekiwane ilości elementów w każdej klasie:
ei = n pi
Gdy jedna z klas jest zawiera mniej liczebności oczekiwanych (ei) niż 5, klasę tę należy połączyć z sąsiednią np. poprzednią. Nie pozostaje nic, jak tylko obliczyć wartość statystyki χ2 oraz porównać obliczoną wartość z wartością krytyczną dla założonego wcześniej poziomu istotności - α (najczęściej równego 0.05; - co odpowiada marginesowi popełnienia błędu 5%), i odpowiedniej liczby stopni swobody - df (ang: degres of freedom).
Pierwszy czynnik już mamy (α = 0.05). Co do liczby stopni swobody to z definicji wiadomo, że jest to wartość obliczana ze wzoru:
df =
k -
p - 1
gdzie:
k - ilość klas wziętych do obliczeń,
p - ilość parametrów szacowanych z próby (jeżeli badamy zgodność rozkładu z rozkładem normalnym, wtedy rozkład możemy wyestymować z dwóch parametrów: średniej i odchylenia standardowego).
Na koniec pozostaje jedynie obliczenie wartości statystyki χ2. Liczymy różnice pomiędzy empirycznymi liczebnościami elementów w poszczególnych klasach szeregu rozdzielczego oraz liczebnościami teoretycznymi wynikającymi z dystrybuanty rozkładu normalnego. Podnosimy je do kwadratu, po czym po prostu sumujemy wartości otrzymane dla wszystkich przedziałów szeregu rozdzielczego.
Jeżeli obliczona wartość jest większa lub równa wartości krytycznej testu odczytanej z tablic rozkładu χ2 (dla założonego poziomu istotności (α) i odpowiedniej liczby stopni swobody (df)),
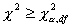
... wtedy istnieją podstawy do odrzucenia hipotezy zerowej. Rozkład populacji genralnej badanej cechy ma najprawdopodobniej wyraźne odstępstwa od normalności.
UWAGA: Należy pamiętać, że w związku z tym, że standardowy rozkład normalny N(0, 1) jest symetryczny względem realizacji zmiennej losowej X równej wartości przeciętnej tej zmiennej (m = 0), w tablicach statystycznych przedstawia się wartości dystrybuanty teoretycznej jedynie dla nieujemnych realizacji tej zmiennej. Zgodnie z własnościami dystrybuanty, gdy zmienna losowa przyjmie wartości ujemne, ich dystrybuantę należy obliczyć wg. wzoru:
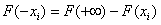 F(-xi) = 1 - F(xi)
F(-xi) = 1 - F(xi)
np.:
F(-2) = 1 -
F(2)
2.4. Badanie zgodności rozkładów empirycznych z rozkładem normalnym za pomocą testu Kołmogorowa-Smirnowa
Test K-S wykorzystuje statystykę λ, która opiera się na porównaniu dystrybuanty empirycznej (kumulanty) ze stablicowaną dystrybuantą teoretyczną, wynikającą z weryfikowanej hipotezy zerowej H0.
Tak jak w przypadku badania zgodności rozkładu empirycznego z wybranym rozkładem teoretycznym za pomocą testu χ2, tak i tutaj, stawiamy hipotezę zerową (H0):
H0: F(ai') = K(ai') (istnieje zgodność pomiędzy dystrybuantami, a więc i rozkładami: empirycznym i teoretycznym).
W przypadku licznych populacji, do weryfikacji hipotezy zerowej wykorzystuje się rozkład (graniczny) statystyki λ:
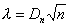
gdzie:
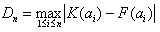
(dla zbiorów licznych), a dla licznych populacji próby:
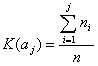
Wypełniamy Tab. 4.
Tab.4. Test λ normalności rozkładu zmiennej X [aa].
| i |
ai [aa] |
ai' |
ni |
K(ai') |
F(ai') |
|K(ai') - F(ai')| |
| 1 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| ... |
|
|
|
|
|
|
| k |
|
|
|
1 |
|
|
| Σ |
- |
- |
n |
- |
- |
- |
gdzie:
i - nr i-tej klasy,
ai - górna granica i-tej klasy,
ai' - zestandaryzowana górna granica i-tej klasy,
ni - liczebność i-tej klasy,
K(ai') - dystrybuanta rozkładu empirycznego (kumulanta) (wg. wzoru),
F(ai') - dystrybuanta rozkładu teoretycznego (odczytywana z tablic dystrybuanty rozkładu teoretycznego np. normalnego),
|K(ai') - F(ai')|- moduł różnic pomiędzy dystrybuantą empiryczną i teoretyczną.
Z tablic rozkładu (granicznego) λ Kołmogorowa odczytujemy wartość krytyczną statystyki λ dla obranego poziomu istotności (λα). Jeżeli spełniony zostaje warunek:
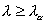
..., wtedy istnieją przesłanki do odrzucenia hipotezy zerowej (H0). Innymi słowy populacja próby nie daje podstaw do stwierdzenia, że populacja generalna charakteryzuje się rozkładem normalnym.