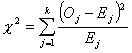Test chi2
Tomasz Bartuś
Test χ2 należy do grupy testów nieparametrycznych. Jego algorytm opiera się na porównaniu częstości zdarzeń wynikających z doświadczenia (empirycznych) ze spodziewanymi. Warunkiem stosowalności testu jest odpowiednio liczna populacja danych. Przyjmuje się, że można go stosować w przypadku populacji większych niż 30 obserwacji. Obostrzenie to wynika z konieczności podziału populacji na klasy i warunku obecności w każdej z klas minimum 5 przypadków (Statistica), (niektórzy (Greń J., 1976) postulują nawet minimum 8 przypadków).
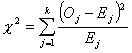
gdzie:
Oj - zdarzenia obserwowane [ang. Observed];
Ej - zdarzenia spodziewane [ang. Expected].
Hipoteza zerowa H0 zakłada, że rozkład zmiennej, którą badamy jest zgodny z danym rozkładem teoretycznym.
Przypuśćmy, że petrograf bada mikroskopowo próbkę cienką jakiejś skały magmowej. Jego zadaniem jest nadanie badanej skale poprawnej nazwy. Do analizy posługuje się planimetrią. Stosując specjalny aparat sprzężony z mikroskopem zlicza 100 kryształów występujących w próbce. Z literatury wiadomo, że w granicie stosunek 4 głównych minerałów ma się do siebie tak jak 4 : 1 : 2 : 3
Mamy odpowiedzieć na pytanie czy badana próbka pozwala na nazwanie SKAŁY granitem?
(skałę w tym momencie traktujemy jako populację generalną, zaś zliczone ilości minerałów jako populację próby).
Stawiamy hipotezę zerową:
H0: Rozkład pomierzonych w skale 100 minerałów jest zgodny z podawanym w literaturze rozkladem dla granitu (4 : 1 : 2 : 3)
My w badaniach statystycznych będziemy oczywiście badać zgodność rozkładów naszych danych z rozkładami normalnym lub logarytmiczno-normalnym.
Obliczamy statystykę χ2 (Tab. 1).
Tab. 1. Obliczenia statystyki χ2
| Minerał |
A |
B |
C |
D |
Σ |
il. obserwowana
[Oj] |
35 |
12 |
22 |
31 |
100 |
il. spodziewanych
[Ej] |
40 |
10 |
20 |
30 |
100 |
| Oj - Ej |
-5 |
2 |
2 |
1 |
- |
| χ2j = (Oj - Ej)2 / Ej |
25/40 |
4/10 |
4/20 |
1/30 |
Σχ2 = 1,258 |
Weryfikacja hipotezy zerowej odbywa się przez porównanie ze znanym, stablicowanym rozkładem χ2. W tablicach statystycznych należy sprawdzić ile w naszym przypadku wynosi wartość krytyczna testu. Jest ona zależna od dwóch czynników:
- założonego wcześniej poziomu istotności - α (prawdopodobieństwo popełnienia błędu I rodzaju (błąd polegający na odrzuceniu hipotezy zerowej, która w rzeczywistości jest prawdziwa). Określa również maksymalne ryzyko błędu, jakie jesteśmy skłonni zaakceptować. Wybór wartości α zależy od nas i od tego jak dokładnie chcemy weryfikować daną hipotezę, najczęściej przyjmuje się α = 0,05 lub 0,01.
- liczby stopni swobody - df (ang: degres of freedom).
Pierwszy czynnik już mamy (α = 0,05). Pozostaje rozpoznanie enigmatycznej nazwy "liczba stopni swobody". Z definicji wiadomo, że jest to wartość obliczana z prostego wzoru:
df =
k -
p - 1
gdzie:
k - ilość klas wziętych do obliczeń,
p - ilość parametrów szacowanych z próby
(jeżeli badamy zgodność rozkładu z rozkładem normalnym, wtedy rozkład możemy wyestymować z dwóch parametrów: średniej i odchylenia standardowego).
W związku z tym, że w naszym przykładzie nie badamy zgodności rozkładu z rozkładem normalnym (ilość szacowanych parametrów z próby był równy 0), wzór na liczbę stopni swobody przybiera nieco zmienioną postać, a mianowicie: df = k - 1. Tak więc dla nas:
α = 0,05
df = 4 - 1 = 3
dla powyższych parametrów z tablicy odczytujemy lub obliczamy wartość krytyczną testu:
χ20.05 = 7,815.
W związku z tym, że nasza wartość testu χ2 wyniosła 1,258 i co za tym idzie spełniony jest warunek:
χ2 < χ20,05, należy stwierdzić, że:
NIE MA PODSTAW DO ODRZUCENIA HIPOTEZY ZEROWEJ H0.
Innymi słowy:
z prawdopodobieństwem 95% można powiedzić, że badana skała jest granitem.
W praktyce badawczej najczęściej spotykamy się z koniecznością zbadania zgodności rozkładów prób z rozkładem normalnym lub lognormalnym. Pakiet Statistica poza informacją na temat wartości testu χ2, podaje także liczbę stopni swobody (df) oraz prawdopodobieństwo p, które można zinterpretować jako prawdopodobieństwo błędu, popełnianego w momencie odrzucenia hipotezy zerowej (mówiącej o zgodności rozkładu próby z jednym z rozkładów teoretycznych).
Tak więc błąd związany z odrzuceniem hipotezy wynosi p ⋅ 100%.
- Jeżeli p ≥ α (α = 0,05) ⇒ Brak podstaw do odrzucenia hipotezy zerowej;
- Jeżeli p < α ⇒ hipotezę zerową odrzucamy;